Nonlinear Patterns and Waves: From Spectra to Stability and Dynamics

Patterns and waves are all around us. Stripes and hexagonal patterns appear on animal coats, as water waves on lakes, on sand dunes in deserts, or in cloud patterns in the sky. Besides being aesthetically pleasing, they often serve important beneficial or detrimental functions. For instance, coherent structures organize transport and mixing in geophysical fluid flows and help facilitate spatial differentiation during the early development of organisms, but they can also lead to tachycardia via reentrant cardiac arrhythmias caused by spiral waves in cardiac tissue.

Perhaps surprisingly, patterns and waves occur in many different systems and on vastly different scales in both time and space, and their dynamic behavior is similar across these systems. Mathematical techniques can help identify the origins and common properties of patterns and waves across various applications. Understanding the ways in which such structures are created can help experimentalists identify the mechanisms that generate them in specific systems; in the case of tachycardia, mathematics may also aid the design of new, less invasive treatments to remove reentrant waves from cardiac tissue.

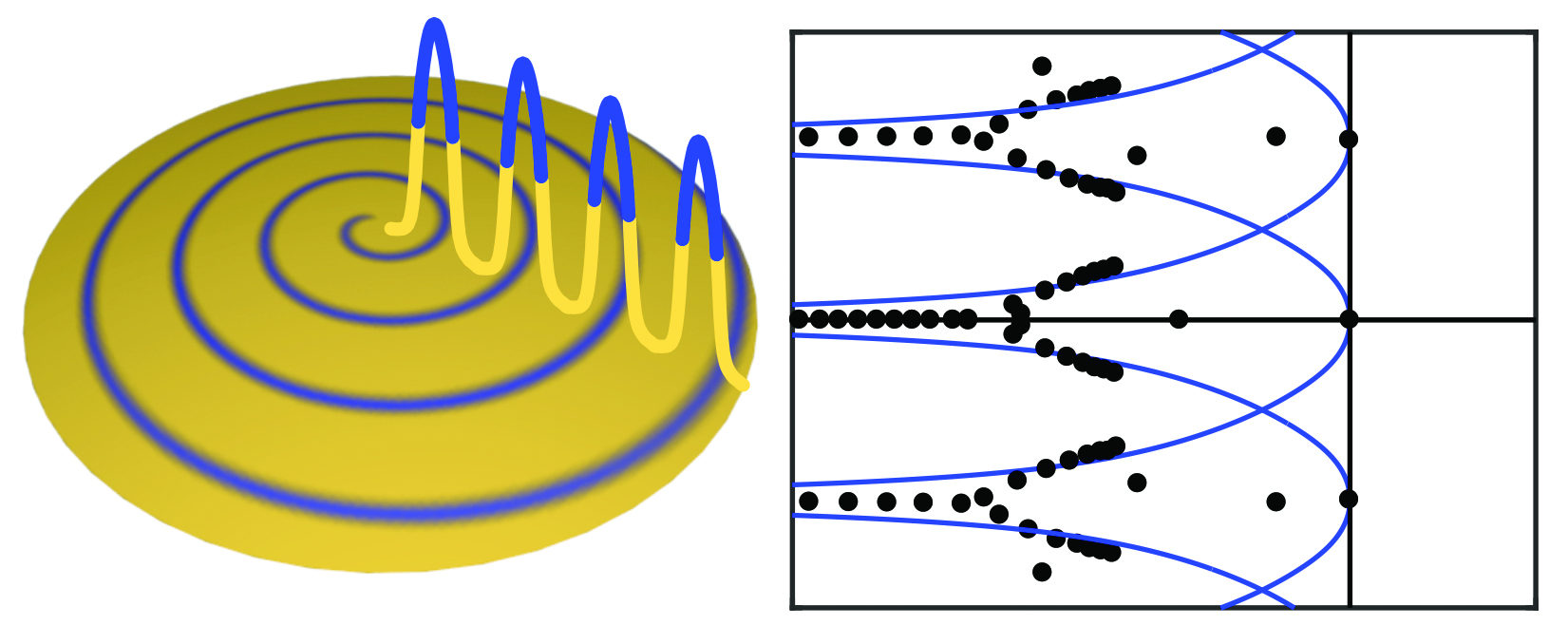
Despite many advances, understanding patterns and waves still poses significant mathematical challenges. To illustrate the difficulties, consider a case in which one has developed a partial differential equations (PDE) model and is interested in assessing the stability of a spiral-wave pattern under small perturbations of its shape. A common strategy in dynamical-systems theory computes the Jacobian of the model evaluated at the underlying pattern, studies its spectrum, and draws conclusions about the nonlinear dynamics based on the spectral properties of this linear differential operator. Using this approach for spiral waves is complicated. For instance, these spectra do not change continuously on the linear level when going from unbounded to large but bounded domains. Furthermore, disentangling the effects of the spiral arms’ modulations in the far field from the movement of the core in the spiral wave’s center is challenging, even on the linear level.

At the 2018 SIAM Annual Meeting, to be held July 9-13 in Portland, Ore., I will show how geometric dynamical systems ideas combined with PDE approaches can shed light on the stability and dynamics of spiral waves and many other patterns and nonlinear waves. I will also discuss applications and open problems.