Numerical Models for Urban Seismic Risk Analysis
Researchers estimate that more than 500,000 detectable earthquakes occur each year; approximately one-fifth of these are felt, and 100 cause damages. An earthquake’s amplitude and duration of induced ground motion, as well as building vulnerability, dictate the number of fatalities and severity of economic loss.
Determining seismic risk—the liability to a built environment from earthquake damage—forms the basis of mitigation strategies. Urban seismic risk, as the name suggests, focuses on specific issues that impact cities. Seismic risk assessment generally involves the quantification of seismic hazard, which is then combined with suitable vulnerability models of structures and facilities for estimating damage probability. Ultimately, a predefined metric measures expected loss.
Mathematical models for seismic hazard quantify the expected earthquake shaking in a given area in terms of various ground motion intensity measures (IMs), such as peak ground acceleration (PGA) or spectral acceleration (SA) response ordinates. PGA is the largest absolute value of ground acceleration that occurs during earthquake shaking at a certain location, whereas SA describes the maximum acceleration of an object (a damped linear oscillator) that is subject to an earthquake and moving along one physical dimension.
For a prescribed building typology (e.g., given structural material, height, and quality), suitable fragility/vulnerability models—which are conditioned on the level of IM and provide the probability of damage/loss—can determine direct physical damage. Our numerical model for risk determination utilizes synthetic earthquake ground motion scenarios and vulnerability models that predict seismic ground motion’s effect on buildings [4]. Here I describe our mathematical approach for seismic risk quantification in densely-populated areas (see Figure 1).
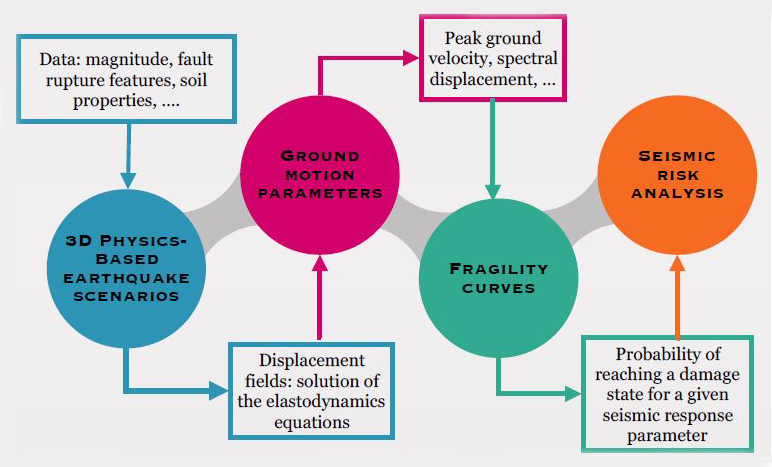
A key element of seismic risk analysis is the characterization of seismic ground shaking and its spatial variability using three-dimensional, physics-based numerical simulations of potential earthquakes with prescribed moment magnitude Mw (measure of the earthquake’s strength), hypocenter location, and source characteristics in the target region.
From a mathematical standpoint, three-dimensional, physics-based models are comprised of partial differential equations that yield the displacement of a (visco) elastic medium—the ground—subjected to an external excitation (seismic) source. The main challenges in the design and analysis of numerical models meant to capture all of the problem’s important physical features while simultaneously retaining affordable costs are as follows: (i) geometric flexibility to correctly describe the complex, three-dimensional features of the domain (the portion of the ground through which seismic waves propagate); (ii) accuracy to capture the media’s heterogeneity and the different spatial and temporal scales; and (iii) scalability to exploit high-performance computing architectures for large-scale computations.
Spectral element (SE) methods are among the most powerful tools in the field of computational seismology. These methods solve problems in a finite-dimensional space made of high-order, piecewise continuous polynomials that are sampled at Gaussian integration points. Further improvement of SE methods for the viscoelasto-dynamics wave propagation equations yield the discontinuous Galerkin spectral element (DGSE) method [1-2]. The main idea of this method relies on a domain decomposition paradigm: the computational domain is partitioned into a number of nonoverlapping substructures, and spectral elements are employed within each subdomain. The discrete solution can remain discontinuous across interfaces, and (weak) continuity is recovered according to the discontinuous Galerkin (DG) paradigm, i.e., by penalizing the jump of the discrete displacement.
This is a very efficient approach for large-scale applications because it keeps the proliferation of numerical unknowns under control, which typically swamps elementwise DG schemes whose finite-dimensional space contains elementwise piecewise discontinuous polynomials. Moreover, the DGSE method in [2] preserves the same accuracy of SE methods and features low numerical dissipation and dispersion errors [3]. This guarantees a precise approximation of both the amplitude and wave-field phase, which provide important information about the interior structure and consistency of soil layers. Additionally, the DGSE method is much more flexible than the SE method, as it allows an adaptive choice of the local (elementwise) discretization parameters, the element size, and the local polynomial degree. The DGSE method also enjoys a high level of intrinsic parallelism, making it well suited for massively parallel computations.
We simulated a number of synthetic earthquake scenarios by varying magnitude, location, and fault-rupture geometry, albeit in a physically consistent way. Each simulated earthquake behaves like a real tremor and provides the full waveform of ground motion at any (sampled) point of the modeled region. One can compute any ground motion IM (e.g., the response spectral displacement) from the synthetic waveform, depending on the class of structures/infrastructures at risk. After computation, we used the selected IM as input to the fragility functions for the target class of structures to determine the probability of exceeding a given damage state. The fragility curve (FC) measures the probability of surpassing certain performance or design criteria as a function of the level of seismic input intensity. It is defined as the conditional probability of a given damage state (DS) that exceeds a threshold \(ds\), based on a value of the ground motion IM, i.e., \(FC(IM, ds)=P(DS \ge ds | IM)\).
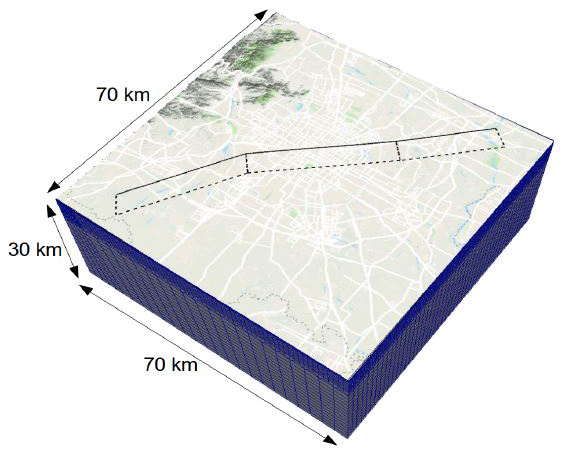
To illustrate the aforementioned workflow, we calculated the seismic hazard/risk analysis of the Beijing metropolitan area. Situated on a sedimentary basin with over 20 million inhabitants, Beijing is one of many megacities that are highly susceptible to seismic threats. The characterization of strong ground motion is hence critical to risk assessment studies in this region. We constructed a three-dimensional numerical model for Beijing by exploiting the following features: (i) the topography model, (ii) the sedimentary base’s depth, (iii) a kinematic representation of potential ruptures breaking the Shunyi-Qianmen-Liangxiang (SQL) fault, and (iv) the three-dimensional velocity profiles. The SQL fault, which lies near downtown Beijing, is 90 kilometers long and has the potential to generate seismic events up to 7.3 Mw.
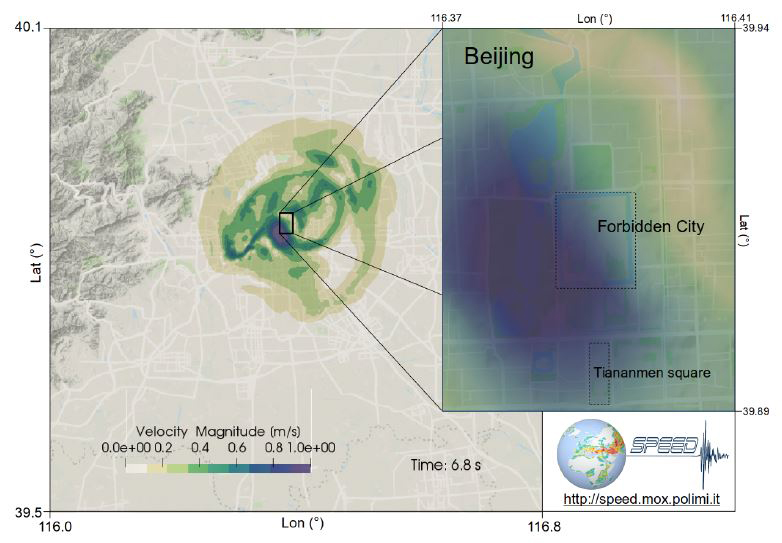
The computational domain, 4,900 square kilometers in area and 30 kilometers deep, consists of approximately 200 million degrees of freedom (see Figure 2). To capture the variability of earthquake ground motion based on different fault rupture scenarios, we performed 30 distinct simulations by varying the magnitude (from 6.5 to 7.3 Mw), hypocenter location, kinematic slip distribution on the fault, and rupture area location. Figure 3 offers a snapshot of the computed peak ground velocity wave-field for a target scenario with magnitude 6.5 Mw. We combined the results of the simulations with the fragility curves for Beijing’s high-rise buildings — the most representative class of structures for seismic risk evaluation. We specifically focused on the so-called super high-rise buildings, which stand over 100 meters tall.
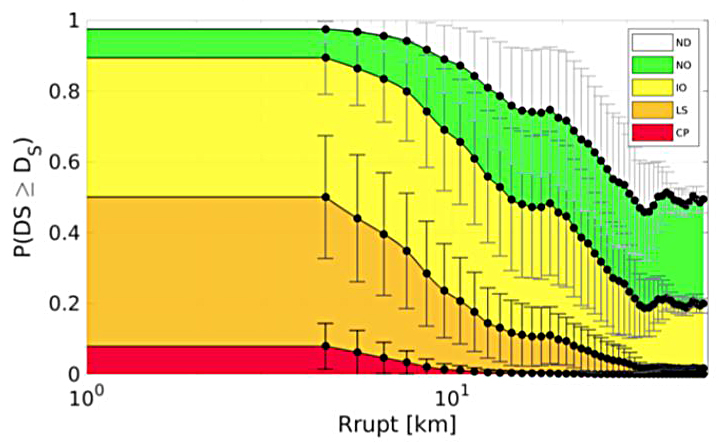
Figure 4 illustrates the probability of exceeding different damage states as a function of the closest distance to the fault rupture for a selected scenario (6.5 Mw). We note a rapid decrease of probability associated with different damage states with respect to fault rupture, and observe a large dispersion around the mean value. Our analysis demonstrates that in the near-field region—especially for rupture distances less than approximately 10 kilometers—the probability of exceeding the life safe and collapse prevention states may be significant, at least based on results obtained within the measured scenarios.
This article is based on the author's invited presentation at the 2019 SIAM Conference on Mathematical & Computational Issues in the Geosciences, which took place earlier this year in Houston, Texas.
Acknowledgments: This research is conducted in collaboration with Paola F. Antonietti, Ilario Mazzieri, and Laura Melas at the Laboratory for Modeling and Scientific Computing MOX in the Dipartimento di Matematica del Politecnico di Milano. More details are available online.
References
[1] Antonietti, P.F., Ferroni, A., Mazzieri, I., Paolucci, R., Quarteroni, A., Smerzini, C., & Stupazzini, M. (2018). Numerical modeling of seismic waves by discontinuous spectral element methods. ESAIM: Proc. Surv., 61, 1-37.
[2] Antonietti, P.F., Mazzieri, I., Quarteroni, A., & Rapetti, F. (2012). Non-conforming high order approximations of the elastodynamics equation. Comput. Meth. Appl. Mech. Eng., 209-212, 212-238.
[3] Ferroni, A., Antonietti, P.F., Mazzieri, I., & Quarteroni, A. (2017). Dispersion-dissipation analysis of 3D continuous and discontinuous spectral element methods for the elastodynamics equation. Geophys. J. Int., 211, 1554-1574.
[4] Melas, L., Antonietti, P.F., Mazzieri, I., Paolucci, R., Quarteroni, A., Smerzini, C., & Stupazzini, M. (2019). Three-dimensional physics-based earthquake ground motion simulations for seismic risk assessment in densely populated urban areas (MOX-Report No. 34/2019). Retrieved from https://www.mate.polimi.it/biblioteca/add/qmox/34-2019.pdf.
About the Author
Alfio Quarteroni
Emeritus professor, Politecnico di Milano and École Polytechnique Fédérale de Lausanne
Alfio Quarteroni is an emeritus professor at the Politecnico di Milano in Italy and École Polytechnique Fédérale de Lausanne in Switzerland. He is the founder of MOX laboratory at Politecnico di Milano and served as its first director from 2002 to 2022. Quarteroni is a SIAM Fellow and a member of the Italian Academy of Science, European Academy of Science, Academy of Europe, Lisbon Academy of Sciences, and Italian Academy of Engineering and Technology. His research interests include mathematical modeling, numerical analysis, scientific computing, and applications in fluid mechanics, geophysics, medicine, and sports performance improvement.

Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



