Optimal Transport for Generative Neural Networks
Since 2012, deep neural networks (DNNs) have been revolutionizing machine learning. Although the concept is far from new, DNNs have enabled spectacular advances in the recognition of text, sounds, images, and videos in recent years. Perhaps even more surprising is that one can also use these neural networks in an unsupervised manner to automatically generate “virtual” text or images, which are often called “deep fakes.” Here I will draw a link between the learning of generative neural networks and the theory of optimal transport. This method, which was framed by Gaspard Monge in the 18th century and reformulated by Leonid Kantorovich in the 20th century, is now a tool of choice for tackling important problems in data science.
Generative Neural Networks
![<strong>Figure 1.</strong> Example of a simplified generative neural network (a network that generates such complex images actually has more layers). Image courtesy of Gabriel Peyré, code courtesy of [1].](/media/c51hr1iw/figure1.jpg)
Rather than use neural networks to analyze images, researchers can employ them “backwards” to generate images [3]. These generative neural networks find applications in special effects, video games, and artistic creation. For example, Figure 1 depicts the structure of a generative network \(g_w\) that depends on weights \(w\). The layers play mirror roles when compared to the architecture of classical discriminating neural networks. Indeed, while networks for discriminating tasks take high-dimensional data (such as an image) and output a low-dimensional representation that is useful for classification, the exact opposite occurs in generative networks. A user can generate an image \(x=g_w(y)\) from a “latent” vector \(y\) that is composed of a small number of values, which are typically drawn randomly.
Training such networks is an unsupervised problem. Consider a large collection of \(n\) training images \(\{z_1, z_2, ..., z_n\}\). The goal is to select the weights \(w\) of the network \(g_w\)'s neurons so the generated “fakes” resemble the training set images as closely as possible. One produces these fake images \((x_i)_i\) by randomly drawing the input latent values \(y_i\) and applying the network to these inputs to obtain \(x_i=g_w(y_i)\). The training optimization problem is therefore
\[\underset{w} \min \,\textrm{Distance}(\{g_w(y_1),...,g_w(y_n)\}, \{z_1,...,z_n\}).\]
We thus wish to define a suitable notion of distance between two sets of points.
Monge’s Optimal Transport
Monge formulated the optimal transport problem in 1781 for military applications [5]. He sought to determine the most economical method of transferring objects from a set of sources \(\{x_1,...,x_n\}\) to a set of destinations \(\{z_1,...,z_n\}\); for Monge, it was a matter of moving soil from cuttings to create embankments for the protection of soldiers. But this scenario finds a multitude of applications. When training generative networks, for example, the fake images that the network generates are the sources and the database’s images are the destinations.
Researchers thus seek a permutation \(s\) of \(\{1,...,n\}\) so that each point \(x_i\) is linked to a single point \(z_{s_i}\). Figure 2 displays a simple example of such a permutation with \(n=6\) elements. Monge’s problem then involves finding the permutation that minimizes the sum of the transport costs. He decided that the cost of transportation between a source \(x\) and a destination \(z\) is equal to the Euclidean distance \(\parallel x-z \parallel\) between the two points. However, one can choose another cost — i.e., a traveling time or the price requirement for gasoline when driving a truck. We must then solve the problem
\[\textrm{Distance}(\{x_1,...,x_n\},\{z_1,...,z_n\}) \overset{\textrm{def}.} = \underset {\textrm{permutation } s} \min \parallel x_1-z_{s_1} \parallel + \parallel x_2 - z_{s_2} \parallel + ... + \parallel x_n - z_{s_n} \parallel.\]
This problem’s solution provides an optimal assignment between the points but also defines the notion of distance between the sets of points in question.
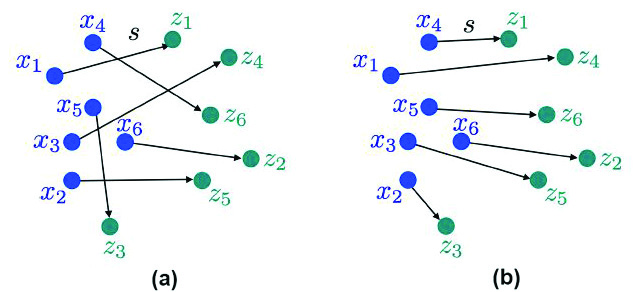
The difficulty of calculating this distance is that the total number of permutations that must be tested is very large; indeed, there are \(n! = n \times (n-1) \times (n-2) \times ... \times 2\times 1\) possibilities. For example, there are \(6!=720\) possible permutations in Figure 2. We can test them all and select the best one, as depicted in Figure 2b. The difficulty is that there are more than \(10^{100}\) possibilities for \(n=70\) — compared to the \(10^{79}\) atoms in the universe. And when training neural networks, \(n\) is even bigger.
Monge was unable to provide an efficient method for solving this problem [5]. Instead, Kantorovich identified a new formulation for the optimal transport problem in 1942 [4]. His formulation allows scientists to divide each source into several parts; for instance, one can split a source into two equal parts, each with a weight \(1/2\). This division of production that simplifies the optimization problem is also natural for Kantorovich’s problem, which attempted to model and plan production in economics. Kantorovich received the Nobel Prize for Economic Sciences for this idea in 1975. In 1947, George Dantzig introduced the simplex algorithm [2], which makes it possible for one to efficiently solve large-scale transport problems. Its numerical complexity when solving an optimal transport problem between \(n\) points is of the order of \(n^3\), which is much lower than \(n!\). The simplex algorithm is at the heart of a large number of industrial systems that must optimize the adequacy between means of production and consumption. Researchers can also use it to train generative neural networks. Further details on optimal transport theory, efficient algorithms, and their application to data science are available in [7].
Adversarial Networks
A difficult aspect of applying optimal transport to create generative networks is choosing the transport cost between two images. One could calculate the Euclidean distance between the images’ pixels, but this method does not work well because it fails to account for the geometry of the objects that are present in the images. In 2014, Ian Goodfellow and his collaborators introduced a more successful idea [3]. In this approach, a second network \(f\)—called an adversary network—plays a discriminative role. While generator \(g\) aims to create fake images that look real, \(f\) plays the role of an opponent that must recognize true and fake images. The joint training of these two networks corresponds to what one may call a zero-sum game. John Nash studied this concept [6]; like Kantorovich, he too received the Nobel Prize in Economic Sciences in 1994.

These recent advances [3] have made it possible for researchers to obtain convincing results in image generation. Figure 3 depicts results from the calculation of “paths” of images between dogs and cats [1]. This “animation” generates a continuous path \(x(t)=g_w((1-t)y_0+ty_1)\) for \(t \in [0,1]\), which is a linear interpolation in latent space between two fixed vectors \(y_0\) and \(y_1\).
This article is based on Gabriel Peyré’s joint plenary address at the 2020 SIAM Annual Meeting and the 2020 SIAM Conference on Imaging Science, which were co-located and took place virtually last year. Peyré’s presentation is available on SIAM’s YouTube Channel.
Acknowledgments: I thank Gwenn Guichaoua for her attentive proofreading, as well as Sébastien Racanière and Vincent Barra for their corrections.
References
[1] Brock, A., Donahue, J., & Simonyan, K. (2019). Large scale GAN training for high fidelity natural image synthesis. In Proceedings of the 2019 international conference on learning representations (ICLR 2019). New Orleans, LA.
[2] Dantzig, G.B. (1990). Origins of the simplex method. In S.G. Nash (Ed.), A history of scientific computing (pp. 141-151). New Nork, NY: Association for Computing Machinery.
[3] Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., …, Bengio, Y. (2014). Generative adversarial nets. In Advances in neural information processing systems (NIPS 2014) (pp. 2672-2680). Montreal, Canada.
[4] Kantorovich, L. (1942). On the transfer of masses. Doklady Akademii Nauk, 37(2), 227-229.
[5] Monge, G. (1781). Mémoire sur la théorie des déblais et des remblais. Histoire de l’Académie Royale des Sciences (pp. 666-704).
[6] Nash, J.F. (1950). Equilibrium points in n-person games. Proc. Nat. Acad. Sci., 36(1), 48-49.
[7] Peyré, G., & Cuturi, M. (2019). Computational optimal transport. Found. Trends Mach. Learn., 11(5-6), 355-607.
About the Author
Gabriel Peyré
Senior Researcher, Centre National de la Recherche Scientifique
Gabriel Peyré is a senior researcher at the Centre National de la Recherche Scientifique (CNRS) and a professor at the École Normale Supérieure. His research is focused on optimal transport methods for machine learning.
Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



