Optimization and Learning with Zeroth-order Stochastic Oracles

Mathematical optimization is a foundational technology for machine learning and the solution of design, decision, and control problems. In most optimization applications, the principal assumption is the availability of at least the first-order derivatives of objective and constraint functions. This assumption is often nonrestrictive, since researchers can use techniques such as automatic differentiation and differentiable programming to obtain derivatives from the mathematical equations that underlie these functions. Derivative-free (or “zeroth-order”) optimization addresses settings wherein such derivatives are not available [5].

Given the pervasiveness of sensors and other experimental and observational data, these types of settings are arising in increasingly more science and engineering domains. For example, consider the ongoing search for novel materials for energy storage. In order to create viable new materials, we must move beyond pure theory and account for the actual processes that occur during materials synthesis. A necessary consequence is that material properties are only available via in situ and in operando characterization. In the context of optimization, this scenario is called a “zeroth-order oracle” — our knowledge about a particular system or property is data driven and limited by the black-box nature of measurement procurement. An additional challenge is that such measurements are subject to random variations, meaning that researchers are dealing with zeroth-order stochastic oracles.

We can compactly express this type of optimization problem as

\[\min_{\mathbf{x} \in \mathbf{R}^n} \mathbb{E}_{\xi}\left[ f(\mathbf{x}; \xi) \right],\]

where \(\mathbf{x}\) denotes the vector of \(n\) decision variables and \(\xi\) is a random variable (e.g., a variable that is associated with the stochastic synthesis and measurement processes). The zeroth-order stochastic oracle is \(f(\mathbf{x}; \xi)\). We can specify values for the random variable only in certain problem settings; in others—such as the laboratory environment in Figure 1—doing so is impossible.

Figure 1 displays an instantiation of a data-driven optimization setting in a chemistry lab at Argonne National Laboratory. An optimization solver specifies a particular composition of solvents and bases, an operating temperature, and reaction times; this combination is then run through a continuous flow reactor. The material that exits the reactor is then automatically characterized through an inline nuclear magnetic resonance detector that illuminates properties of the synthesized materials. These stochastic, zeroth-order oracle outputs return to the solver in a closed-loop setting that minimizes wasted product and accelerates materials discovery. Figure 2 illustrates this closed-loop (or “online”) optimization.

One of the main techniques in derivative-free optimization is the use of model-based methods, which utilize zeroth-order outputs to form surrogate models that are expressly built and adaptively updated for optimization [3]. Users can perform new queries of the oracle based on these models, which model-based algorithms then employ to evolve the trust region, i.e., the area in which a model is presumed to be trustworthy for optimization purposes. Such techniques are becoming progressively more commonplace when the oracle outputs are deterministic and optimization takes place over no more than a few dozen decision variables.

When the oracle is stochastic, we must reconsider the typical interpolation-based surrogate models and algorithmic dynamics. Stochastic settings also reduce the decision variable dimensions that one can effectively address when compared to deterministic, noise-free oracles. As the number of variables grows, optimization incurs an increasingly large overhead—in terms of both the linear algebraic operations and the number of oracle queries—that is associated with the creation and maintenance of surrogate models in high-dimensional spaces.

Randomized strategies for deterministic optimization problems, like Coralia Cartis and Lindon Roberts’ approach [1], enable work in substantially lower-dimensional spaces. These methods typically use ideas from sketching to provide a dimension reduction at each iteration that results in significantly smaller overhead. By applying results such as the Johnson–Lindenstrauss lemma, we can show that—with large probability—a reduced gradient will be small in magnitude only if the full-space gradient is small as well. Consequently, the performance of model-based, trust-region iterations in reduced spaces has provable implications for the full space wherein the optimization problem resides. Because of this randomized dimension reduction, algorithmic convergence is now based on probabilistic analysis.

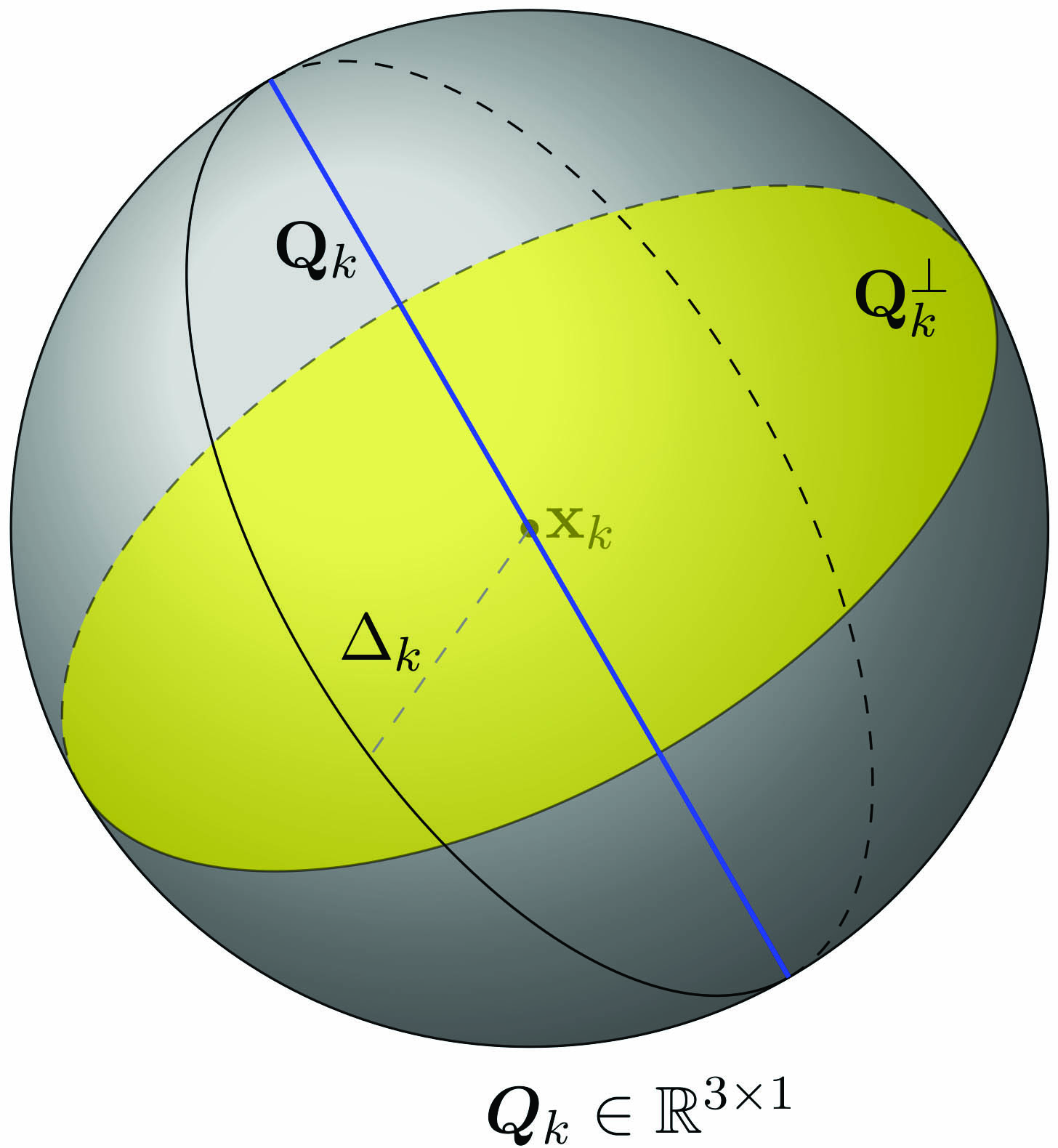
Such techniques can greatly increase the range of decision variable dimensions for which zeroth-order deterministic problems are solvable in practice. For example, Figure 3 depicts the way in which a subproblem that would have been posed in a three-dimensional trust region is now posed in a one-dimensional trust region that is defined by a randomized sketching matrix \(Q_k\). 

When the zeroth-order oracle is stochastic, two sources of randomness occur in algorithms: (i) Randomness due to the algorithm’s sketching and (ii) randomness from realizations of the stochastic oracle. We must carefully separate these two sources, but it is again possible to show that extensions of such zeroth-order algorithms are convergent on stochastic optimization problems [4].

This result allows researchers to address stochastic optimization problems with hundreds of decision variables, rather than mere handfuls. It also expands the scope for the solution of complex stochastic data-driven problems, including the tuning of variational algorithms on emerging quantum computers.

Stefan Wild presented this research during an invited talk at the 2022 SIAM Annual Meeting, which took place in Pittsburgh, Pa., last summer. 

Acknowledgments: This work is partially based on efforts that are supported by the Applied Mathematics Program in the Office of Advanced Scientific Computing Research at the U.S. Department of Energy’s Office of Science.

References

[1] Cartis, C., & Roberts, L. (2022). Scalable subspace methods for derivative-free nonlinear least-squares optimization. Math. Program.
[2] Chang, T.H., & Wild, S.M. (2022). ParMOO: Python library for parallel multiobjective simulation optimization. Retrieved from https://parmoo.readthedocs.io.
[3] Conn, A.R., Scheinberg, K., & Vicente, L.N. (2009). Introduction to derivative-free optimization. In MOS-SIAM series on optimization. Philadelphia, PA: Society for Industrial and Applied Mathematics.
[4] Dzahini, K.J., & Wild, S.M. (2022). Stochastic trust-region algorithm in random subspaces with convergence and expected complexity analyses. Preprint, arXiv:2207.06452.
[5] Larson, J., Menickelly, M., & Wild, S.M. (2019). Derivative-free optimization methods. Acta Numer., 28, 287-404.