Perpetual Motion and the Theorem of Cosines

What follows is the first installment of a regular column by Mark Levi of the Pennsylvania State University. As proposed a few months ago, the column will consist of “short mathematical/physical morsels which should be of interest to any curious person, including graduate students, and requiring the attention span of a few minutes only . . . and always with pictures.” At SIAM News we liked the idea immediately, based in part on Levi’s recent article presenting a newly discovered connection between bicycle tracks and the stationary Schrödinger equation, which was based in turn on his invited talk at SIAM’s 2013 conference on dynamical systems. We were also favorably impressed by a category labelled “Some Nifty Things.”  

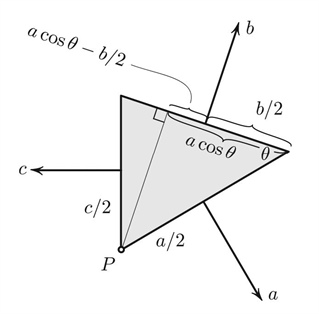
The “machine” is a rigid triangular container in flatland, free to pivot on a vertex \(P\) (Figure 1). As a thought experiment, we fill the triangle with compressed gas. The trapped gas tries to rotate each side of the rigid frame around \(P\). 

The sum of the three torques is zero (the alternative would be a functioning perpetual motion machine)––and this is the theorem of cosines in disguise. Indeed, deciphering the zero-torque statement we have, according to Figure 1:

\[\begin{equation}\tag{1}c ~c/2 + b(a ~cos~ \theta − b/2) = a~ a/2,\end{equation}\]

or, after a quick rearrangement:

\[\begin{equation}\tag{2}
c^2 = a^2 + b^2 − 2ab~ cos~ \theta.
\end{equation}\]

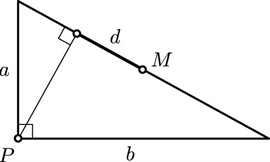
The same idea leads us to discover that for a right triangle we have

\[\begin{equation}
b^2 − a^2 = 2cd,
\end{equation}\]

in the notation of Figure 2.

An amusing exercise in the same spirit is to translate the equilibrium statement for the half-disk shown at the right into a formula.

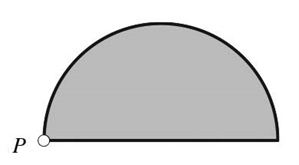
\[\int^{\pi/2}_{0}~\mathrm{sin}\theta~\mathrm{cos}\theta~d \theta - 1/2.\]