Persistent Homology Identifies Tumor Shapes to Enhance Prognostic Precision

Cancer research has established that a tumor’s shape impacts its growth, spread, and response to treatment. Traditional imaging techniques often use various summary values to describe tumor size and shape, but they tend to overlook nuanced geometric details. Our study leverages topological data analysis—specifically persistent homology—to extract invariant shape features from medical images that reveal underlying patterns in tumor growth and ultimately help predict patient survival risk.

Unlike traditional shape descriptors, persistent homology captures topological and geometric features of data across multiple scales. These features—which include connected components, loops, and voids—remain stable under scale-preserving transformations like rotation and translation. Essentially, persistent homology employs a multiscale topological lens to analyze shapes and identify local and global shape patterns.

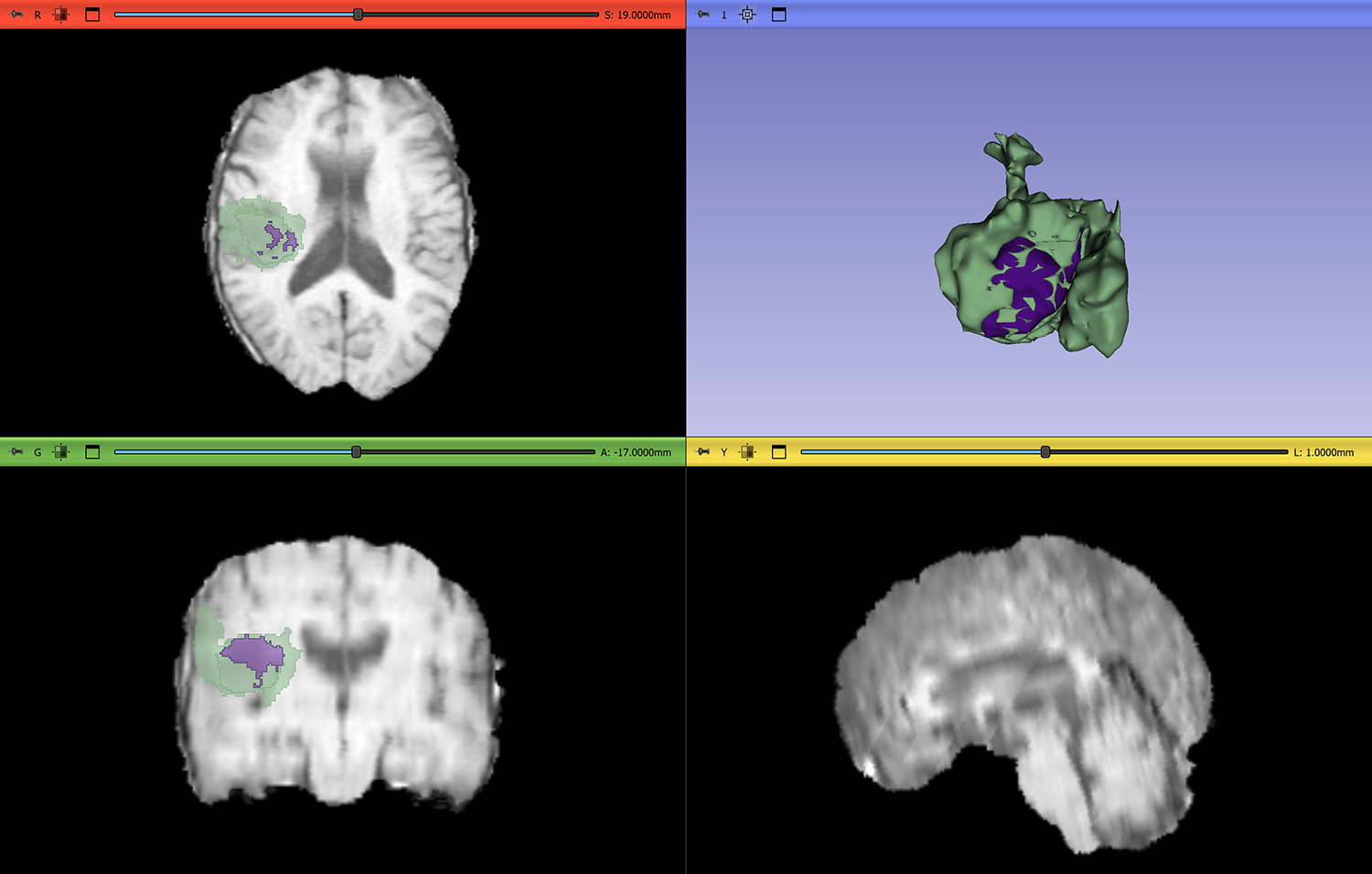
Our work utilizes the multimodal Brain Tumor Segmentation dataset, which segments brain tumor regions of three-dimensional magnetic resonance imaging scans into the categories of enhancing tumor, necrotic core, and edema. For simplicity, our study considers three specific classes: enhancing tumor, non-enhancing tumor, and non-tumor (see Figure 1). 

The three-class image exemplified in Figure 1 does not itself reveal any shape information, such as particulars about connectivity and size. To discern these details from segmented images, we propose the three-class signed Euclidean distance transform (SEDT-3). SEDT-3 assigns a value to each pixel based on the shortest distance to the nearest pixel of a different class. The sign of the SEDT-3 value depends on the pixel class: values are respectively negative, positive, and infinite for non-enhancing tumors, enhancing tumors, and non-tumors. Since these values recover the size, connectivity, and relative location between neighboring pixels, we can use them to construct a cubical complex in order to compute persistent homology. 

Persistent homology records the appearance and disappearance of topological features over the filtration of the signed distance. The resulting persistence diagram plots the birth of specific topological features on the x-axis and their subsequent death on the y-axis. Figure 2 displays a three-class two-dimensional tumor image, its signed distance, a sequence of cubical complices, and the resulting persistence diagrams. 

The persistent homology output—i.e., the persistence diagram—summarizes various aspects of the image, including size, shape, and connectivity between the enhancing and non-enhancing tumor regions. However, the unstructured data format of persistence diagrams makes them difficult to integrate as inputs into statistical or machine learning models. To address this issue, we smooth and weight the diagrams to transform them into a functional space that represents the information from the shape space. We can then analyze the functional space via well-established statistical methods.

To evaluate the impact of tumor shape on patient survival, we introduce a functional spatial Cox proportional hazards model (FCoxPH) that integrates topological shape features as functional predictors and combines them with spatial data that reflects the tumor’s location in the brain. The model considers spatial information that is specific to regions like the frontal lobe, thus acknowledging tumor placement’s significant influence on survival outcomes. It also incorporates clinical variables such as patient age, sex, and Karnofsky Performance Scale score—which measures one’s ability to perform daily activities—to create a more comprehensive predictive model. The application of functional principal component analysis and the \(L_1\)-regularization approach promotes model sparsity.

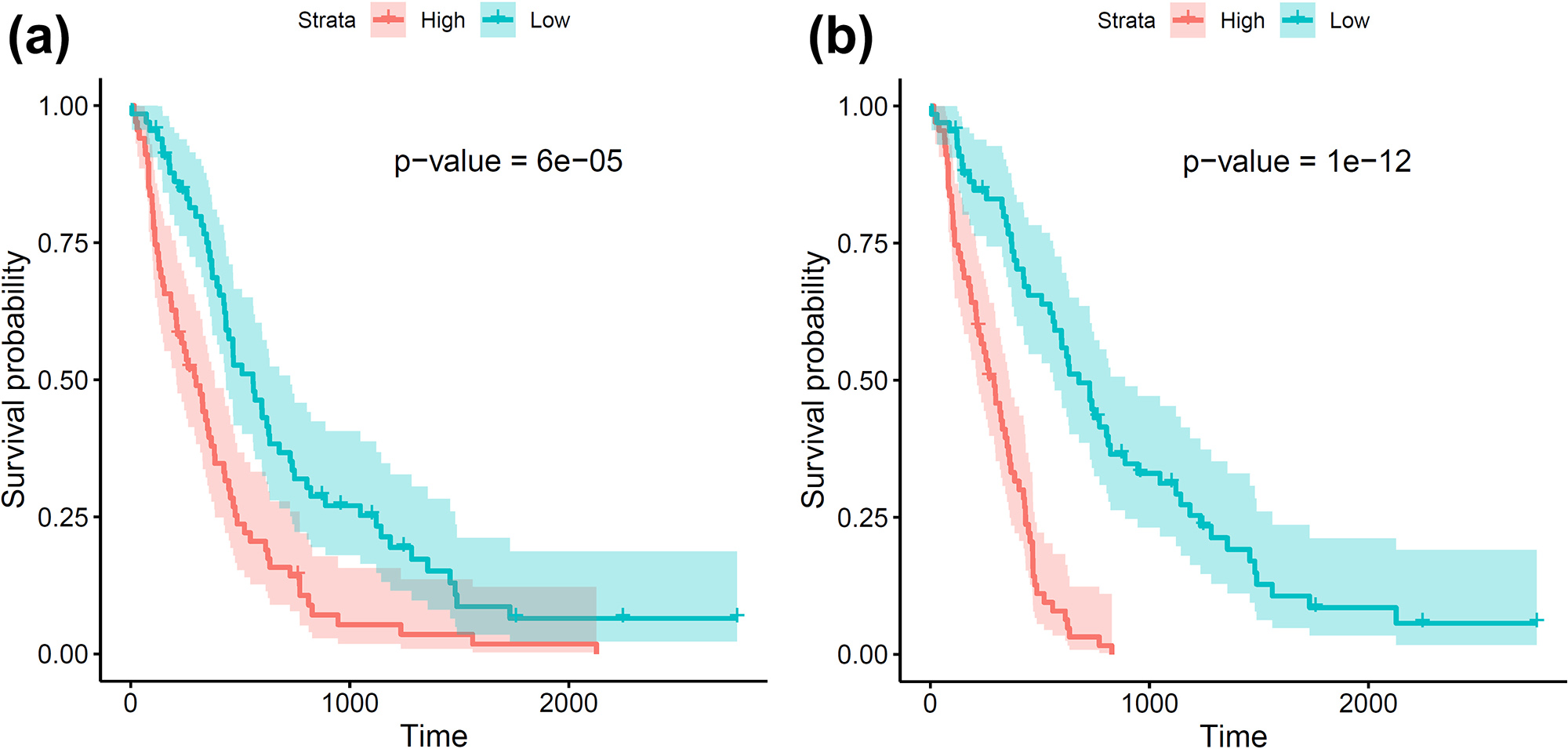
Our study compares two survival models: (i) the Cox proportional hazards (CoxPH) model with clinical variables and (ii) the aforementioned FCoxPH model with clinical variables and topological shape features. The leave-one-out cross validation technique predicts risk scores of brain tumor patients for both models; we then assign the patients to either the high- or low-risk group based on this score. The Kaplan-Meier plots in Figure 3 depict the survival probability over time for the two models; we see that the FCoxPH model produces more accurate predictions than the CoxPH model. 

Our proposed approach identifies specific topological shape features that correlate with poor prognoses in brain tumor patients. For example, tumors that exhibit a higher number of small, connected non-enhancing tumor regions and small- to medium-sized enhancing tumor regions in the frontal lobe tend to be associated with an increased risk of death. The FCoxPH model enables researchers and clinicians to interpret the links between particular shape characteristics and patient survival probability, offering valuable insights for prognosis and treatment planning.

Ultimately, we demonstrate that topological data analysis has the potential to help automate the identification of high-risk brain tumor shapes and serve as a rapid risk assessment tool in clinical settings. Future research could generalize our approach to assess the malignancy and progression of different tumor types—such as lung and breast cancers—or apply this technique to other predictive tasks, like the identification of gene mutations. By identifying high-risk shape features that might otherwise go unnoticed, persistent homology could hence become a valuable healthcare tool that supports personalized treatment plans for patients with cancer.

Chul Moon delivered a minisymposium presentation on this research at the 2024 SIAM Conference on Mathematics of Data Science, which took place in Atlanta, Ga., last October.

References
[1] Moon, C., Li, Q., & Xiao, G. (2023). Using persistent homology topological features to characterize medical images: Case studies on lung and brain cancers. Ann. Appl. Stat., 17(3), 2192-2211.