Plug-and-Play: A General Approach for the Fusion of Sensor and Machine Learning Models
Regularized or Bayesian inversion has revolutionized our ability to reconstruct images from incomplete data. For example, suppose that we want to reconstruct an image \(x\) from a vector of sensor measurements \(y\), given by
\[y=Ax+w,\]
where \(A\) is a linear forward model and \(w\) is additive white Gaussian noise with variance \(\sigma^2\). The regularized reconstruction then comes from
\[\hat{x} = \underset {x} {\textrm{argmin}} \left\{ \frac{1}{2\sigma^2} \parallel y -Ax \parallel^2 + h(x) \right\} ,\]
where \(h(x)\) is a term that encourages a “regular” solution.
But how should we choose the regularizing function \(h(x)\)? If we select \(h(x)=-\log p(x)\), where \(p(x)\) is an assumed prior distribution, \(\hat{x}\) then becomes the Bayesian maximum a posteriori (MAP) reconstruction. Other reasonable choices for \(h(x)\) include the total variation or Markov random field cost functions. However, the simplistic nature of these analytical priors—which do not always accurately represent the true distribution of real image collections—often limits the quality of the resulting MAP reconstructions.
Over the last decade, image denoisers such as block-matching and 3D filtering—and more recently, convolutional neural network denoisers—have demonstrated that dramatic improvements in denoising performance are possible with the use of increasingly complex image operations. These advanced denoising algorithms effectively model the distribution of real images but do not utilize any explicit cost function \(h(x)\). This raises the following question: How can we fuse the traditional models of regularized inversion with the implicit models of modern denoising algorithms?
Plug-and-play (PnP) methods answer this question by providing a framework for fusing traditional sensor models with black-box models. These black-box models can range from advanced denoising algorithms that are used as priors to more general “agents” that are typically trained via machine learning methods, like deep neural networks.
Model Fusion with Plug-and-Play
We can express the MAP reconstruction in the simpler and more general form of
\[\hat{x}= \underset {x} {\textrm{argmin}} \{f(x)+h(x)\},\tag1\]
where \(f(x) = \frac {1}{2\sigma^2} \parallel y-Ax \parallel^2\) is the sensor term and \(h(x)\) is again the regularizing prior model term.
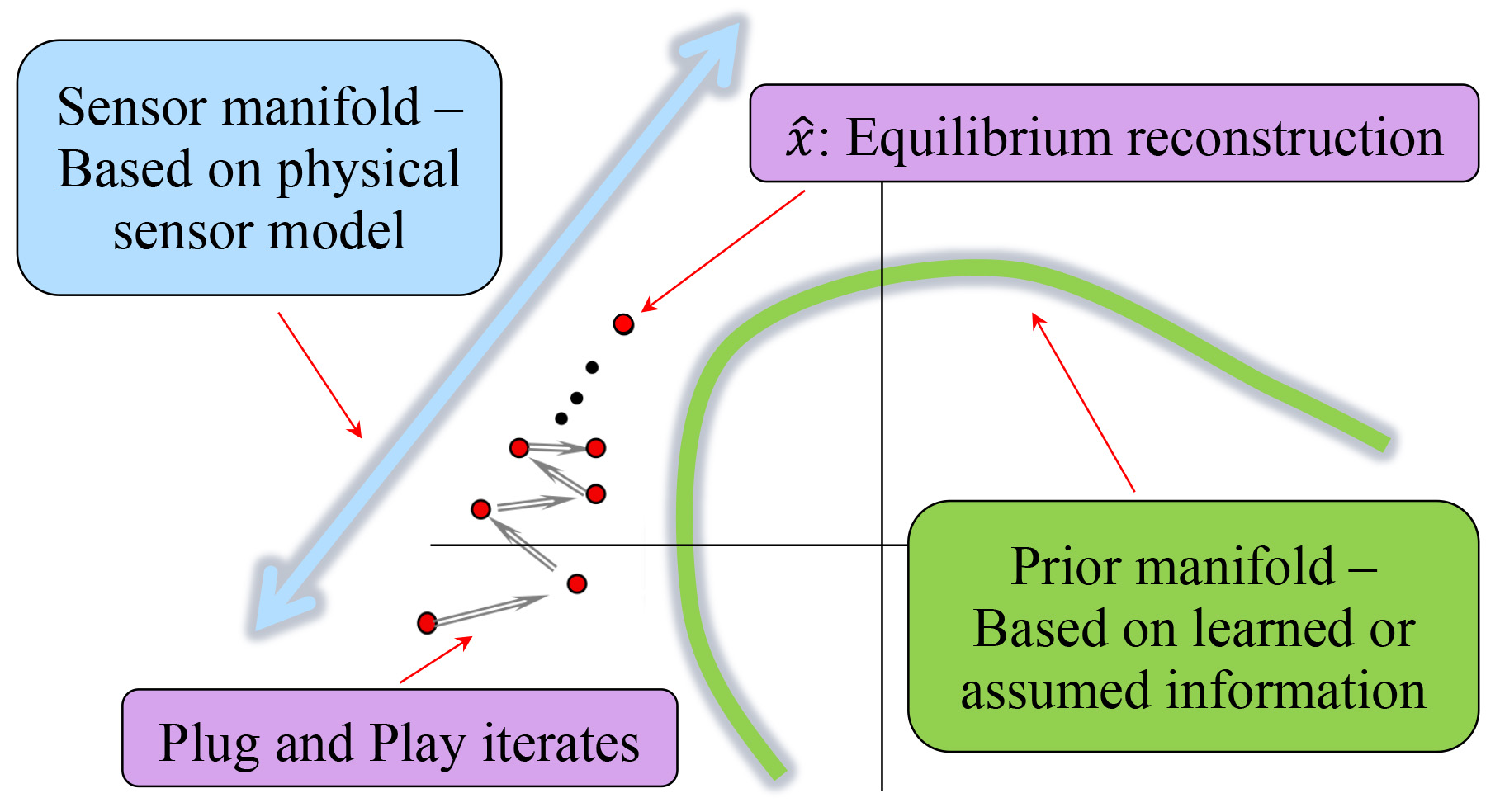
Figure 1 graphically illustrates this equation with a sensor manifold that corresponds to small values of \(f(x)\) and a prior manifold that corresponds to small values of \(h(x)\). The MAP reconstruction is thus at a location that minimizes the distance to both manifolds, making it maximally consistent with the data and prior.
The important special case of image denoising occurs when \(A=I\). In this case, the observations \(y\) consist of \(x\) plus additive Gaussian white noise and the MAP reconstruction is given by \(\hat{x}=H(y)\), where
\[H(y)=\underset {x} {\textrm{argmin}} \left\{\frac{1}{2\sigma^2}\parallel y-x \parallel^2 +h(x) \right\}.\]
The key insight of PnP is that the denoiser \(H(y)\) is also the proximal map of \(h(y)\). That is, \(H\) is an operator that takes a step to reduce \(h\) while maintaining proximity to the input point.
Interestingly, we can use the well-known alternating direction method of multipliers (ADMM) algorithm to solve our MAP optimization problem by alternately applying \(H\) along with a second forward model proximal map that comes from
\[F(v)= \underset {x} {\textrm{argmin}} \left\{ f(x) + \frac {1}{2\sigma^2} \parallel x-v \parallel^2 \right \}.\]
The ADMM algorithm for solving \((1)\) is then given by the following iteration:
\[\textrm{Repeat} \{\] \[x \leftarrow F(v-u)\tag2\] \[v \leftarrow H (x+u)\tag3\] \[u \leftarrow u+x-v\tag4\] \[\}.\]
We obtain the PnP algorithm by simply replacing the original proximal map \(H(y)\) with a novel black-box operator and running the new algorithm. Therefore, “plugging in” a black-box or learned denoiser \(H(x)\) yields a new algorithm with the same outer loop but a fresh interpretation.
Again, Figure 1 illustrates the intuition behind PnP. Alternating applications of the plug-in operator \(H(x)\) and the forward model proximal map \(F(x)\) move the solution between the sensor and data manifolds in a zig-zag sequence that converges to a fixed point under appropriate hypotheses. When \(H(x)\) is a black-box denoiser, this fixed point no longer minimizes a cost function; however, one can view it as reaching an equilibrium.
In this sense, PnP is a meta-algorithm — it takes existing algorithms for function minimization and converts them into new algorithms that use more general input-output maps. The basic idea of PnP [3, 4] has been applied to a wide variety of problems in several application domains with excellent results.
Multi-Agent Consensus Equilibrium
A shortcoming of PnP is that it is a solution without a problem. The original ADMM algorithm was designed to minimize the MAP cost function; but after replacing some components with black-box operators, there is no longer any cost function to minimize.
To address this issue, we introduce equilibrium methods that determine a system of equations to solve rather than a function to minimize. The basic form of consensus equilibrium (CE) stems from the converged solutions of the updates in \((2)\)-\((4)\). When converged, it must be true that \(x^* = v^*\). This substitution yields CE equations that define the problem that the PnP algorithm solves [1]:
\[x^* = F(x^*-u^*)\] \[x^* = H(x^*+u^*).\]
Since \(H\) is a denoiser and \(x\) is the reconstructed image, we can interpret \(u\) in this context as noise that is removed in the operation \(x^*=H(x^*+u^*)\).
When \(H(x)\) is a general black-box operator and not a proximal map, this system of equations no longer determines a cost function’s minimum. However, the CE equations do determine a well-defined equilibrium condition. So we see that the goal of PnP methods is not to solve the optimization problems of traditional regularized inversion. Instead, they aim to solve more general and flexible sets of equilibrium equations.
Multi-agent consensus equilibrium (MACE) generalizes PnP to the case of more than two agents. It defines a stacked operator of agents \(\mathbf{F}\), along with a consensus operator \(\mathbf{G}\) that computes the average of its inputs. These operators are given by
\[\mathbf{F}(\mathbf{w}) = \left[ F_1(w_1), \ldots, F_K(w_K) \right]^T \; \textrm{and} \; \mathbf{G}(\mathbf{w}) =\left[ \frac{1}{K} \sum_k w_k, \ldots, \frac{1}{K} \sum_k w_k \right]^T,\]
where each agent \(F_k(w_k)\) is intuitively designed to move the solution closer to some desired goal. The MACE equations then take the simple form of
\[\mathbf{F}(\mathbf{w}^*)=\mathbf{G}(\mathbf{w}^*).\]
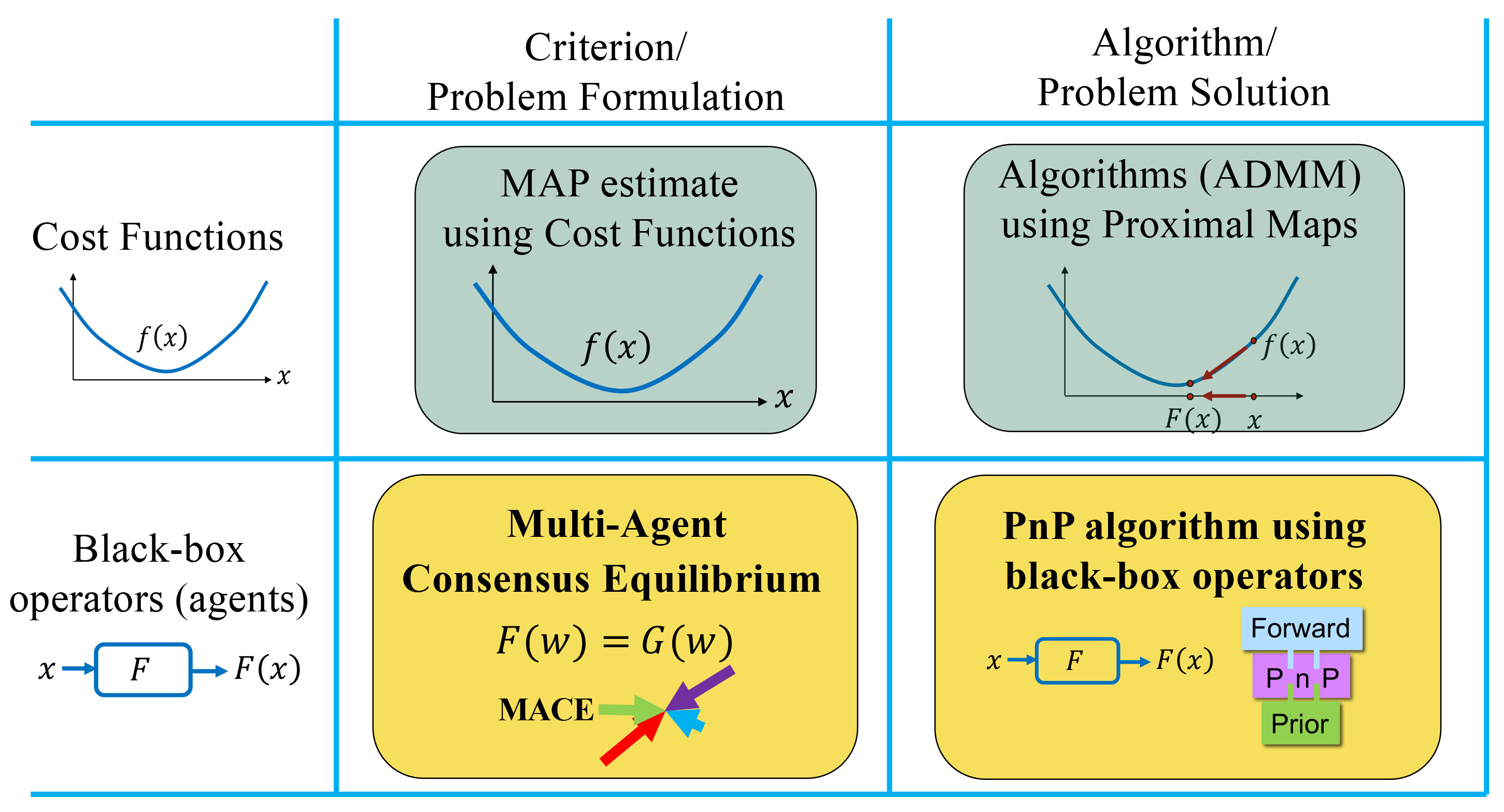
Figure 2 presents an overview of MACE’s role by separating the ideas into four categories: criterion versus algorithm and cost functions versus agents. MACE completes the matrix by providing criteria for the formulation of problems that are based on agent equilibrium rather than simply on cost function minimization.
In summary, PnP is a framework that incorporates modern black-box operators into regularized inversion problems. And MACE delivers a problem criterion in the form of equilibrium equations that the PnP algorithm solves. The aforementioned PnP and MACE methods are just the first steps in a range of new techniques that fuse traditional models with emerging machine learning and algorithmic models. Code that illustrates these methods is available in [2].
This article is based on Charles A. Bouman’s SIAM Activity Group on Imaging Science Best Paper Prize Lecture at the 2020 SIAM Conference on Imaging Science, which took place virtually last year. Bouman’s presentation is available on SIAM’s YouTube Channel.
Acknowledgments: Charles A. Bouman and Gregery T. Buzzard were partially supported by NSF CCF-1763896. Brendt Wohlberg was supported by Los Alamos National Laboratory’s Laboratory Directed Research & Development Program under project number 20200061DR.
References
[1] Buzzard, G.T., Chan, S.H., Sreehari, S., & Bouman, C.A. (2018). Plug-and-play unplugged: Optimization-free reconstruction using consensus equilibrium. SIAM J. Imag. Sci., 11(3), 2001-2020.
[2] Buzzard, G.T., Wohlberg, B., & Bouman, C.A. (2021). PnP and MACE reference implementation. Software library available at https://github.com/gbuzzard/PnP-MACE.
[3] Sreehari, S., Venkatakrishnan, S.V., Wohlberg, B., Buzzard, G.T., Drummy, L.F., Simmons, J.P., & Bouman, C.A. (2016). Plug-and-play priors for bright field electron tomography and sparse interpolation. IEEE Trans. Comput. Imag., 2(4), 408-423.
[4] Venkatakrishnan, S.V., Bouman, C.A., & Wohlberg, B. (2013). Plug-and-play priors for model based reconstruction. In 2013 IEEE global conference on signal and information processing (pp. 945-948). Austin, TX: IEEE.
About the Authors
Charles A. Bouman
Showalter Professor, Purdue University
Charles A. Bouman is the Showalter Professor of Electrical and Computer Engineering and Biomedical Engineering at Purdue University and a member of the National Academy of Inventors. His research inspired the first commercial model-based iterative reconstruction system for medical X-ray computed tomography.

Gregery T. Buzzard
Professor, Purdue University
Gregery T. Buzzard is a professor of mathematics at Purdue University, where he served as department head from 2013-2020. His research focuses on analysis and algorithms for adaptive measurement and reconstruction.
Brendt Wohlberg
Senior Research Scientist, Los Alamos National Laboratory
Brendt Wohlberg is a senior research scientist in the Theoretical Division at Los Alamos National Laboratory. His research centers on foundations and algorithms for imaging inverse problems.
Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



