Prime Gap Breakthrough

Bounded Gaps Between Primes: The Epic Breakthroughs of the Early Twenty-First Century. By Kevin Broughan. Cambridge University Press, Cambridge, U.K., April 2021. 590 pages, $49.99.

In Bounded Gaps Between Primes, Kevin Broughan of the University of Waikato has written a remarkably comprehensive account of the 2013 landmark discovery that demonstrated the existence of infinitely many disjoint real intervals of length at most \(L\) that contain two or more prime numbers. The originally reported length was \(L = 7 \times {10^7}\), but follow-up efforts reduced that figure to \(246\) by 2014. Some have noted that proving the Elliott-Halberstam conjecture would cause a further reduction to \(L = 6\). 

Yet both \(L = 246\) and \(L = 6\) are still far from \(L = 2\), which would settle the twin primes conjecture that Alphonse de Polignac first enunciated in 1849. If nothing else, the new results appear to suggest that the long-unapproachable conjecture may be settled in the not-too-distant future.

Broughan provides a table of 17 publications on prime gaps, the first 11 of which appeared between 1923 and 1988. From 2006 to 2009, two more papers introduced new methods but failed to eliminate the possibility that \(\lim \inf_n({p_{n+1}} - {p_n}) = \infty\), where \(p_n\) is the \(n^{\rm{th}}\) prime in the list that begins with \(p_1 = 2\). The last four tabulated papers—published in 2013 and 2015—reduced \(L\) successively from \(7 \times {10^7}\) to \(4{,}680\), then to \(600\), and finally to \(246\). The authors were Yitang Zhang, a collective known as Polymath8a, James Maynard and Terence Tao, and a second collective known as Polymath8b.

In 2009, Timothy Gowers proposed the Polymath idea in a blog entry entitled, “Is massively collaborative mathematics possible?” He suggested that anyone with thoughts about a specific problem should speak up, even if their ideas are undeveloped or likely wrong. After all, the knowledge that a large group can bring to a given problem is considerably greater than the knowledge of just one or two individuals. Gowers even proposed a short list of problems for which massive collaboration seemed suitable.

Although Broughan traces the twin primes conjecture back to its apparent roots, he focuses on developments from the present century. Bounded Gaps Between Primes offers brief biographical sketches of the main contributors to prime gaps literature and directs interested readers to more extensive interviews that are available elsewhere. By far the most poignant sketch is that of Zhang, who obtained the original estimate \(L \le 7 \times {10^7}\). Born in 1955, Zhang grew up in mainland China during the Cultural Revolution. Unable to go to school, he taught himself with whatever books he could find and later attended Peking University, where he became a star student. Zhang came to the U.S. in the 1980s and earned a Ph.D. from Purdue University in 1991. But the job market was unwelcoming and he worked odd jobs to support himself until 1999, when he became an adjunct professor at the University of New Hampshire teaching introductory calculus. Through it all, Zhang’s mathematical curiosity remained unrelenting.

Hardy and Little-wood’s 1923 paper is the first entry in Broughan’s table; this publication proved the existence of infinitely many values of \(n \le x\) for which

\[{p_{n + 1}} - {p_n} \le \left( {\frac{2}{3}\: + \:o\left( 1 \right)} \right)\log x.\tag1\]

The constant \(2/3\) was subsequently improved numerous times before Daniel Alan Goldston, Yoichi Motohashi, János Pintz, and Cem Yalçın Yıldırım (GMPY) replaced the right side of \((1)\) first with \(o(\log x)\) and then with \(C{(\log x)^{\frac{1}{2}}}{(\log\log x)^2}\) for an appropriate constant \(C\). Hardy and Littlewood also conjectured that

\[{\pi _2}(x)\sim C' x/{(\log x)^2}\tag2\]

for an appropriate \(C'\), where \({\pi _2}(x)\) is the number of primes \(p \le x\) such that \(p + 2\) is also a prime. They were led to this conjecture by Cramér’s suggestion that a randomly chosen natural number between \(1\) and \(x\) should be prime with probability \(1/\log x\). That result, together with an observation by L.E. Dickson, yielded a significant generalization.

Dickson noticed that certain patterns among the primes occasionally repeat themselves and conjectured that some do so infinitely often. The patterns that he noticed take the form \(\mathcal{H} = \left\{ {{h_1},{h_2},\: \ldots \:,{h_k}} \right\}\) and are such that numerous translates \(\mathcal{H} + n = \left\{ {{h_1} + n,\: {h_2} + n,\: \ldots \:,{h_k} + n} \right\}\) consist exclusively of primes. \(\mathcal{H}\) must satisfy certain conditions to behave in this manner. For instance, all of the differences \({h_i} - {h_j}\) must be even because if even one difference were odd, \(\mathcal{H}\) and every translate of \(\mathcal{H}\) would contain an even (non-prime) number. Dickson separated the set of all possible patterns \(\mathcal{H}\) into two subsets: an “inadmissible” subset that could never perform in the proposed manner and an “admissible” subset that conceivably might. The pattern \(\mathcal{H} = \{0,2\}\) belongs to Dickson’s admissible set and corresponds to the twin primes conjecture. Zhang’s proof that \(L \le 7 \times {10^7}\) utilizes an \(\mathcal{H}\) of dimension \(k = 3.5 \times {10^6}\).

The so-called Dickson-Hardy-Littlewood conjecture generalizes the original Hardy-Littlewood conjecture by asserting that

\[\pi \left( {x,{\cal H}} \right) = \# \left\{ {n \le x:\left( {n + {h_1}, \: \ldots ,\: n + {h_k}} \right) \in {\mathbb{P}^k}} \right\}\sim g\left( {\mathcal{H}} \right) \cdot x/{(\log x)^k},\tag3\]

where \(\mathbb{P}\) denotes the collection of all primes and \(g\left( \mathcal{H} \right)\) is readily computable. If confirmed, this would imply both the twin primes conjecture and the fact that \(p + \left\{ {0,\:2,\:6} \right\}\) and \(p + \left\{ {0,\:4,\:6} \right\}\) consist of primes alone for infinitely many primes \(p\). However, \(p + \left\{ {0,\:2,\:4} \right\}\) is known to consist exclusively of primes for at most a finite number of \(p \in \mathbb{P}\). And for every \(k \in \mathbb{N}\), there are infinitely many \(k\)-tuples \(\mathcal{H}\) in Dickson’s admissible set.

From time immemorial, sieves have been the tool of choice for the study of primes. Broughan suspects that a general theory of sieves—with applications to branches of mathematics beyond number theory—might someday exist. At the moment, however, there are many different sieves. In addition to the sieve of Eratosthenes and Adrien-Marie Legendre’s variation, Bounded Gaps Between Primes mentions eight important sieves — most of which have useful variants.

Modern sieves estimate \(S\left( {A,\mathcal{P},z} \right) = \# \left\{ {a \in A:\left( {a,\mathcal{P}\left( z \right)} \right) = 1} \right\}\). Here, \((a,b)\) denotes the greatest common divisor of \(a\) and \(b\), \(\mathcal{P}\) is an infinite set of primes, \(\mathcal{P}(z)\) is the product of all primes in \(\mathcal{P}\) that do not exceed \(z\), and \(A = \{ {a_1}, \ldots ,{a_n}\}\) is a finite sequence of natural numbers. If one “sifts” \(A\) by removing all elements that share a prime factor with \(\mathcal{P}(z)\), \(S(A,\mathcal{P},z)\) is the number of surviving elements of \(A\). If \(A_q=\{a_n \in A: q|a_n\}\) while \(\mu(\cdot)\) is the so-called Möbius function, one may write

\[S(A,\mathcal{P},z)=\Sigma_{q|\mathcal{P}(z)}\mu(q)|A_q|.\tag4\]

This is an exact version of the Brun sieve. In the special case \(\mathcal{P}=\mathbb{P}\)—the set of all prime numbers—set \(S(A,z):=S(A, \mathbb{P},z)\). Then if \(A=\mathbb{N} \bigcap [1,x]\) and \(\sqrt{x} \notin \mathbb{P}\), 

\[S(A, \sqrt{x})=\pi(x)-\pi(\sqrt{x}).\tag5\]

This is Legendre’s form of the sieve of Eratosthenes, obtained by appealing to the combinatorial principle of inclusion and exclusion.

Mathematician Viggo Brun used his sieve to attack both the twin primes conjecture and the older Goldbach conjecture. By the end of the decade, he was able to show that the sum of the reciprocals of the twin primes converges and that there exist infinitely many natural numbers \(n\), such that both \(n\) and \(n+2\) have at most nine prime factors. While Brun’s sieve continues to find occasional applications, Atle Selberg’s proposed sieve around 1940 has contributed far more to prime gap breakthroughs.

The distinguishing feature of Selberg’s sieve for the estimation of \(S(A, \mathcal{P},z)\) is a sequence \(\{\lambda_q\}\) that is defined as follows: \(\lambda_1=1\) and \(\lambda_q=0\) if either \(q \ge z\) or \(q\) fails to divide \(\mathcal{P}(z)\). Otherwise, \(\lambda_q\) may be any real number. Since \(\mathcal{P}(z)\) is a product of distinct primes, \(q<z\) only fails to divide \(\mathcal{P}(z)\) if \(q\) contains a repeated prime factor. Unless \(q\) is “square free,” \(\lambda_q\) may be any real number. The quantities \(\lambda_q\) attracted Selberg’s attention because

\[S(A, \mathcal{P},z)\le \sum_{a\in A}(\sum_{q|(a,\mathcal{P}(z))}\lambda_q)^2=|A|Q+R,\tag6\]

where \(Q\) is a quadratic form in the \(\lambda_q s\). As many as 40 percent thereof are potentially nonzero quantities, which one may choose to minimize the upper bound \((6)\).

GMPY’s 2006 paper was celebrated in number theory circles for its use of admissible \(k\)-tuples, appeal to the Elliott-Halberstam conjecture, and optimization step, all of which have since found applications elsewhere. Zhang’s reading of this paper, along with its 2009 sequel, appears to have pointed the way to \(L \le 7 \times 10^7\). 

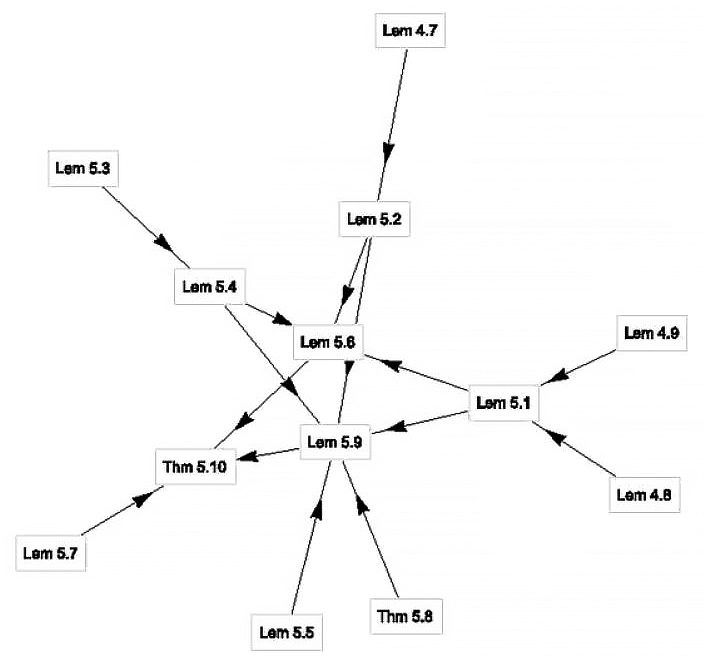
Broughan explains that Zhang’s result was accepted almost immediately by experts in the field precisely because it did not make extensive use of novel or unfamiliar techniques. Instead, it leveraged a surprising amount of the machinery that mathematicians have developed for the study of prime numbers. For example, the Elliott-Halberstam conjecture involves a parameter \(\theta \in [0,1]\); the conjecture is known to be true for \(0\le \theta \le 1/2\) and false for \(\theta =1\). In order to complete his proof, Zhang had to prove it true for \(0 \le \theta \le 1/2+1/1168\). Figure 1 illustrates the complex nature of Zhang’s proof and depicts the logical dependencies among the various theorems and lemmas. Zhang’s result is denoted “Thm 5.10.” Several of the contributing results are simply variations of those already known to workers in the field. For instance, Theorem 5.8 is Zhang’s variation of a theorem due to Bombieri and Vinogradov that seems to underlie every approach to the study of prime gaps.

Everything discussed in this review is contained in the first few chapters of Bounded Gaps Between Primes. The later chapters are meant to encompass all content that a novice might wish to know before beginning work in the field. The material is therefore quite technical, precise, and rich in detail. Broughan’s treatise will likely remain a standard reference for many years to come.