Protecting Privacy with Synthetic Data

Researchers across every scientific discipline need complete and reliable data sets to draw trustworthy conclusions. However, publishing all data from a given study can be undesirable. For example, medical data in particular include personal information that—if published in full—would violate patients’ privacy and potentially expose them to harm. Similarly, many studies in the social sciences include demographic or geographical data that could easily be exploited by unscrupulous parties.

In short, researchers must strike a delicate balance between publishing enough data to verify their conclusions and protecting the privacy of the people involved. Unfortunately, multiple studies have shown that simply anonymizing the data—by removing individuals’ names before publication, for instance—is insufficient, as outsiders can use context clues to reconstruct missing information and expose research subjects. “We want to generate synthetic data for public release to replace the original data set,” Bei Jiang of the University of Alberta said. “When we design our framework, we have this main goal in mind: we want to produce the same inference results as in the original data set.”

In contrast with falsified data, which is one of the deadliest scientific sins, researchers can generate synthetic data directly from original data sets. If the construction process is done properly, other scientists can then analyze this synthetic data and trust that their conclusions are no different from what they would have obtained with full access to the original raw data — ideally, at least. “When you [create] synthetic data, what does it mean to be private yet realistic?” Sébastien Gambs of the University of Québec in Montréal asked. “It’s still an open research question.”

During the 2022 American Association for the Advancement of Science Annual Meeting, which took place virtually in February, Jiang and Gambs each presented formal methods for the generation of synthetic data that ensure privacy. Their models draw from multiple fields to address challenges in the era of big data, where the stakes are higher than ever. “There is always a trade-off between utility and risk,” Jiang said. “If you want to protect people [who] are at a higher risk, then you perturb their data. But the utility will be lowered the more you perturb. A better approach is to account for their risks to begin with.”

Unfortunately, malicious actors have access to the same algorithmic tools as researchers. Therefore, protection of confidentially also involves testing synthetic data against the types of attacks that such players might utilize. “In practice, this helps one really understand the translation between an abstract privacy parameter and a practical guarantee,” Gambs said. In other words, the robustness of a formal mathematical model is irrelevant if the model is not well implemented.

Differential Privacy Made Simple(r)

Gambs and his collaborators turned to differential privacy: a powerful mathematical formalism that in principle is the best available technique for securing confidentiality. However, the approach is also complex and difficult to implement without a high degree of statistical knowledge. To smooth the edges, Gambs’ team combined differential privacy with a probabilistic concept known as vine copula—drawn from a model that mathematician Abe Sklar first published in 1959 [4]—and applied the method to real data to demonstrate its usefulness.

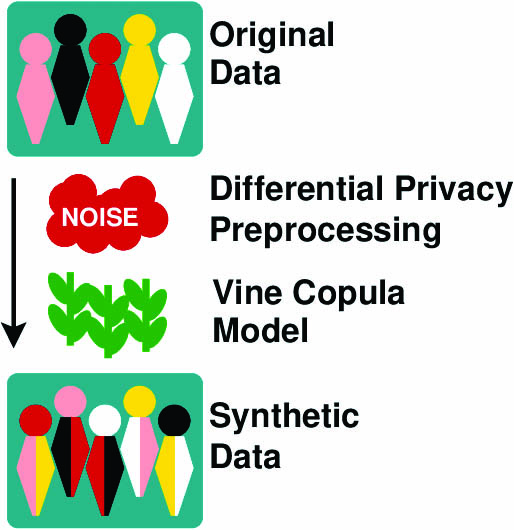
In pure differential privacy applications,¹ researchers add a judicious amount of noise that is scaled by a parameter \(\varepsilon\) to the original data set in order to disrupt correlations between variables that could identify sensitive information. Though this framework offers the strongest possible privacy guarantee in formal terms, it has a number of practical drawbacks. “One issue with differential privacy is keeping as much utility as possible,” Gambs said. “It’s abstract in the sense that the mathematics and the [privacy] guarantee are very formal. It’s difficult for people who use this method to understand what it means to choose a particular value of \(\varepsilon\) in terms of what they’re protecting from privacy attacks.”

Gambs and his colleagues wanted their toolkit to be extremely user-friendly and flexible so that researchers without expertise in formal privacy mathematics can apply it to their own data [1]. Their algorithm first preprocesses the raw data via differential privacy methods and a preselected noise “budget,” then follows up with the vine copula technique on the scrambled data set to produce the final synthetic tables for analysis (see Figure 1). The group also applies known types of attacks to their own synthetic data sets to ensure that their security levels are sufficient. “When you use differential privacy, you have some assumptions about the distribution of the data that are not necessarily true in real life,” Gambs said. “Instead, you might have a subpopulation [with] a high correlation between profiles. If you just rely on the theoretical guarantee of differential privacy but don’t do any practical privacy attacks, you might miss this kind of problem in the data.”

Striving for Maximum Usefulness

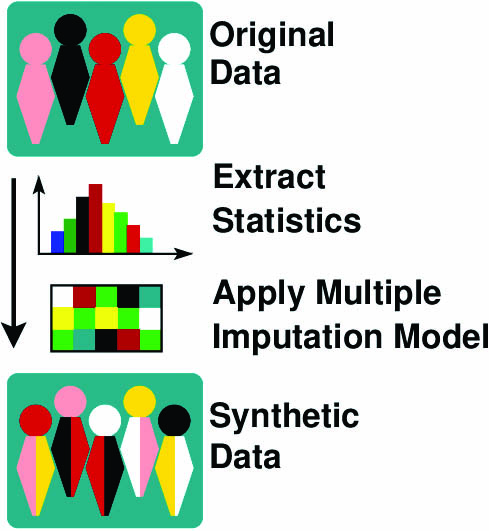
Jiang found that the differential privacy framework is actually too powerful in many respects, particularly in medical studies for rare diseases where the number of participants may be fewer than 1,000. In these cases, it is paramount to protect subjects’ identities while still drawing scientifically valid conclusions. “The noise added to the data set [for differential privacy] is usually huge,” she said. “This means that you may not get the same inference results by using the synthetic data set.”

Instead, her team chose a model that preserves the statistical conclusions between the raw data and the synthetic data set [2]. Their method is based on the multiple imputation (MI) framework that statistician Donald Rubin originally proposed in the 1980s to draw inferences from data sets with missing entries [3]. Jiang and others turned this framework inside out; they began with existing complete data, built a model for it, then utilized MI to generate synthetic data (see Figure 2). “MI is a missing data framework, but we don’t have missing data in the sense that the data provider actually has access to the private data set,” Jiang explained. “Our framework takes this fact into account, and then we generate additional data based on private data. Because the model is always correctly specified, we can maintain information in our synthetic data. This is the novelty of our approach.”

The synthetic data set has the exact same statistical characteristics as the original data because of its construction process. But Jiang warned that this method is most valuable for small studies; more data begets a greater possibility for users to identify correlations between variables, even when the data themselves are artificial. The next phase of research involves circumventing this limitation.

Testing the Defenses

Governments around the world (including in Canada, where both Jiang and Gambs are based) increasingly require their funded research projects to publish all data. This demand is laudable in general terms, as openness aids replicability and trust in science. Yet in addition to the general need to refrain from exposing private information like names and addresses, researchers also do not want to inadvertently hurt participants in other ways. In particular, multiple forms of discrimination are legal — some U.S. states allow companies to fire LGBTQ+ employees, for example. Many scientific studies need to account for drug usage, sex work, and other widespread activities, and subjects rightfully hesitate to participate if they know that they are at risk of exposure. Employers too often skirt the law even when discrimination is illegal, such as for disability, pregnancy, or chronic illness. These actions make participant protection even more crucial during data publication.

With these concerns in mind, Jiang, Gambs, and their collaborators are investigating ways to prevent both inadvertent exposure and malicious privacy attacks. Regardless of which method is best for the research at hand, the goal remains the same: do not hurt your subjects to obtain a scientific conclusion.

¹ In a previous SIAM News article, Matthew Francis wrote about differential privacy and the U.S. census. 

References

[1] Gambs, S., Ladouceur, F., Laurent, A., & Roy-Gaumond, A. (2021). Growing synthetic data through differentially-private vine copulas. Proc. Priv. Enh. Technol., 2021(3), 122-141.
[2] Jiang, B., Raftery, A.E., Steele, R.J., & Wang, N. (2022). Balancing inferential integrity and disclosure risk via model targeted masking and multiple imputation. J. Am. Stat. Assoc., 117(537), 52-66.
[3] Rubin, D.B. (1987). Multiple imputation for nonresponse in surveys. Hoboken, NJ: Wiley & Sons.
[4] Sklar, A. (1959). Fonctions de répartition à n dimensions et leurs marges. Publ. Inst. Statist. Univ. Paris, 8, 229-231.