Proving Existence Is Not Enough: Mathematical Paradoxes Unravel the Limits of Neural Networks in Artificial Intelligence

The impact of deep learning (DL), neural networks (NNs), and artificial intelligence (AI) over the last decade has been profound. Advances in computer vision and natural language processing have yielded smart speakers in our homes, driving assistance in our cars, and automated diagnoses in medicine. AI has also rapidly entered scientific computing. However, overwhelming amounts of empirical evidence [3, 8] suggest that modern AI is often non-robust (unstable), may generate hallucinations, and can produce nonsensical output with high levels of prediction confidence (see Figure 1). These issues present a serious concern for AI use within legal frameworks. As stated by the European Commission’s Joint Research Centre, “In the light of the recent advances in AI, the serious negative consequences of its use for EU citizens and organisations have led to multiple initiatives [...] Among the identified requirements, the concepts of robustness and explainability of AI systems have emerged as key elements for a future regulation.”

Robustness and trust of algorithms lie at the heart of numerical analysis [9]. The lack of robustness and trust in AI is hence the Achilles’ heel of DL and has become a serious political issue. Classical approximation theorems show that a continuous function can be approximated arbitrarily well by a NN [5]. Therefore, stable problems that are described by stable functions can be solved stably with a NN. These results inspire the following fundamental question: Why does DL lead to unstable methods and AI-generated hallucinations, even in scenarios where we can prove that stable and accurate NNs exist?

Our main result reveals a serious issue for certain problems; while stable and accurate NNs may provably exist, no training algorithm can obtain them (see Figure 2). As such, existence theorems on approximation qualities of NNs (e.g., universal approximation) represent only the first step towards a complete understanding of modern AI. Sometimes they even provide overly optimistic estimates of possible NN achievements.

The Limits of AI: Smale’s 18th Problem

The strong optimism that surrounds AI is evident in computer scientist Geoffrey Hinton’s 2017 quote: “They should stop training radiologists now.” Such optimism is comparable to the confidence that surrounded mathematics in the early 20th century, as summed up in David Hilbert’s sentiment: “Wir müssen wissen. Wir werden wissen” [“We must know. We will know”].

Hilbert believed that mathematics could prove or disprove any statement, and that there were no restrictions on which problems algorithms could solve. The seminal contributions of Kurt Gödel [7] and Alan Turing [12] turned Hilbert’s idealism upside down by establishing paradoxes that expedited impossibility results about the feasible achievements of mathematics and digital computers.

A similar program on the boundaries of AI is necessary. Stephen Smale already suggested such a program in the 18th problem on his list of mathematical problems for the 21st century: What are the limits of AI? [11]. As we gain a deeper appreciation of AI’s limitations, we can better understand its foundations and acquire a stronger sense of direction for exciting new AI techniques. This is precisely the type of growth that happened with the work of Gödel and Turing, which respectively lead to many modern foundations and modern computer science.

By expanding the methodologies of Gödel and Turing, we initiate a foundations program about the boundaries of AI and demonstrate limitations on the existence of randomized algorithms for NN training [4]. Despite many results that establish the existence of NNs with excellent approximation properties, algorithms that can compute these NNs only exist in specific cases.

Desirable NNs May Exist

Classical approximation theorems show that NNs can approximate a continuous function arbitrarily well [5]. In response, we might initially expect few restrictions on the scientific problems that NNs can handle. For example, consider the least absolute shrinkage and selection operator (LASSO) problem

\[\Xi(y) = \mathrm{argmin}_{x \in \mathbb{C}^{N}} \hspace{3mm} \lambda\|x\|_{l^1}+\|Ax-y\|_{l^2}^2, \qquad \lambda > 0\tag1\]

for a fixed \(A \in \mathbb{R}^{m \times N}\) with variable \(y \in \mathbb{R}^m\). Can we train a NN to solve this problem? Let us consider a simple scenario wherein we have a collection \(\mathcal{S}=\{y_k\}_{k=1}^R\) and want to compute a NN \(\varphi: \mathbb{R}^m \rightarrow \mathbb{R}^N\), such that \(\mathrm{dist}(\varphi(y_k),\Xi(y_k))\leq \epsilon\) for some accuracy parameter \(\epsilon > 0\) and any \(y_k\in\mathcal{S}\).

Here, \(\mathrm{dist}(x,\Xi(y))\) denotes the \(l^2\)-distance of \(x \in \mathbb{R}^m\) to the solution set \(\Xi(y)\). We take the word “compute” literally, meaning that a computer can never exactly give \(A\) and the \(y_k\)s;  for example, an entry of \(A\) could be an irrational number. Even if \(A\) and the \(y_k\)s are all rational, the overwhelming majority of software runs floating-point arithmetic in base-2. The training data that is available to an algorithm is thus the collection of all \(\mathcal{T} = (\{A_n\}_{n\in\mathbb{N}},\{y_{k,n}\}_{k \leq R, n\in\mathbb{N}})\), such that \(\|A-A_n\| \leq 2^{-n}\) and \(\|y_k - y_{k,n}\| \leq 2^{-n}\), i.e., an arbitrary precision approximation of the dataset. By denoting the suitable collection of NNs with \(\mathcal{NN}\), it follows easily from classical approximation theory that a mapping \(\Phi\) exists with

\[\Phi(\mathcal{T}) = \varphi_{\mathcal{T}}\in\mathcal{NN}, \quad \text{where} \quad  \varphi_{\mathcal{T}}(y) \in \Xi(y) \quad \forall \, y \in \mathcal{S}.\tag2\]

This formula raises the following question: If we can prove the existence of a NN with great approximation qualities, can we find the NN with a training algorithm?

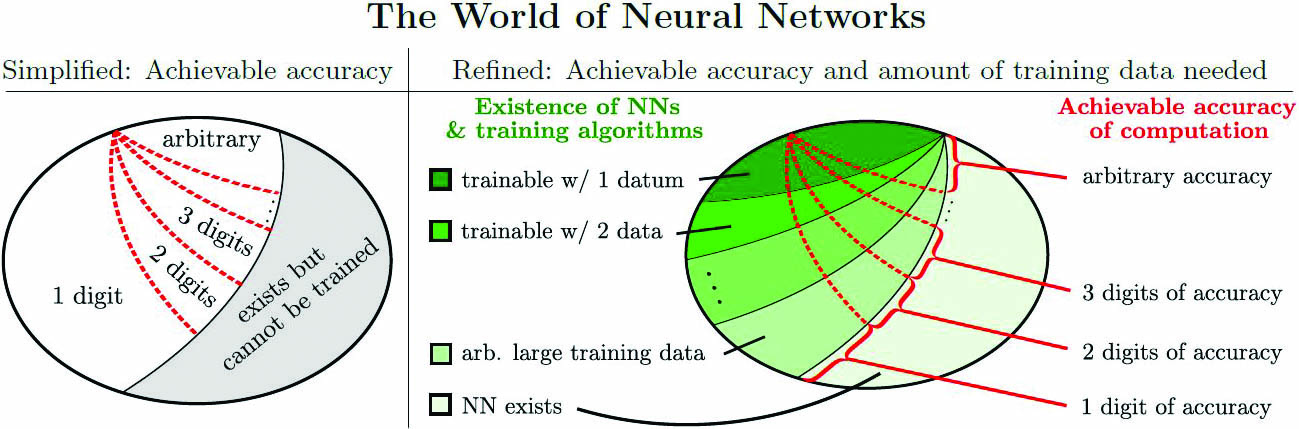
But They May Not Be Trainable

The answer to the aforementioned question is “no,” but for quite subtle reasons. Consider the earlier LASSO problem \((1)\). While a NN for this problem provably exists—as in \((2)\)—it generally cannot be trained by an algorithm [4]. Pick any positive integers \(K\geq 3\) and \(L\). Well-conditioned classes of datasets, such that \((2)\) is true, do then exist. Yet regardless of computing power and the data’s precision levels, we have the following:

(i) Not trainable: No algorithm, not even one that is randomized, can produce a NN with \(K\) digits of accuracy for any member of the dataset with a probability greater than \(1/2\).

(ii) Not practical: \(K-1\) digits of accuracy is possible over the whole dataset, but any algorithm that trains such a NN requires arbitrarily large training data.

(iii) Trainable and practical: \(K-2\) digits of accuracy is possible over the whole dataset via an algorithm that only uses \(L\) training data, regardless of the parameters.

Figure 3 depicts a Venn diagram of the intricate world of NNs that is based on the above results. We try to compute the existing accurate NN in Figure 4, even though we know that doing so is impossible.

The SCI Hierarchy

The techniques that prove our results stem from the seminal work of Gödel and Turing, with generalizations and extensions from the Solvability Complexity Index (SCI) hierarchy [2]. The SCI hierarchy and its accompanying tools allow users to obtain sharp boundaries of algorithms’ abilities. We expand upon and refine some of the tools that are associated with this hierarchy, as well as the mathematics behind Smale’s extended 9th problem about linear programs [1, 11]. To prove our results, we also introduce and develop the theory of sequential general algorithms. General algorithms are a key tool within the SCI hierarchy, and sequential general algorithms broaden this concept and capture the notion of adaptive and/or probabilistic choices of training data.

The Boundaries of AI Through Numerical Analysis

Any theory seeking to understand the foundations of AI must be aware of methodological limitations. This realization is increasingly apparent. “2021 was the year in which the wonders of artificial intelligence stopped being a story,” Eliza Strickland wrote in IEEE Spectrum. “Many of this year’s top articles grappled with the limits of deep learning (today’s dominant strand of AI) and spotlighted researchers seeking new paths.”

Given the rich history of establishing methodological boundaries via condition numbers, backward errors, precision analysis, and so forth, it is natural to turn to numerical analysis for a solution. We must design a program about the boundaries of AI through numerical analysis to determine the areas wherein modern AI can be made robust, secure, accurate, and ultimately trustworthy. Due to methodological boundaries, such a program cannot include all areas. The formidable question is thus: When can modern AI techniques provide adequate robustness and trustworthiness? The answer to this query will shape political and legal decision making and significantly impact the market for AI technologies. 

Moreover, we cannot determine this theory solely with the extensive collection of non-constructive existence theorems for NNs, as evidenced by the previous impossibility result. The big challenge is identifying the NNs that are not only stable and accurate, but can also be computed by algorithms. This collection is a small subset of the collection of NNs that are proven to exist. 

References

[1] Bastounis, A., Hansen, A.C., & Vlačić, V. (2021). The extended Smale’s 9th problem – On computational barriers and paradoxes in estimation, regularisation, computer-assisted proofs and learning. Preprint, arXiv:2110.15734.
[2] Ben-Artzi, J., Colbrook, M.J., Hansen, A.C., Nevanlinna, O., & Seidel, M. (2020). Computing spectra – On the solvability complexity index hierarchy and towers of algorithms. Preprint, arXiv:1508.03280.
[3] Choi, C.Q. (2021, September 21). 7 revealing ways AIs fail. IEEE Spectrum. Retrieved from https://spectrum.ieee.org/ai-failures.
[4] Colbrook, M.J., Antun, V., & Hansen, A.C. (2022). The difficulty of computing stable and accurate neural networks: On the barriers of deep learning and Smale’s 18th problem. Proc. Nat. Acad. Sci., 119(12), e2107151119.
[5] DeVore, R., Hanin, B., & Petrova, G. (2021). Neural network approximation. Acta Numer., 30, 327-444.
[6] Finlayson, S.G., Bowers, J.D., Ito, J., Zittrain, J.L., Beam, A.L., & Kohane, I.S. (2019). Adversarial attacks on medical machine learning. Science, 363(6433), 1287-1289.
[7] Gödel, K. (1931). Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Monatshefte Math. Phys, 38(1), 173-198.
[8] Heaven, D. (2019). Why deep-learning AIs are so easy to fool. Nature, 574(7777), 163-166.
[9] Higham, N.J. (2002). Accuracy and stability of numerical algorithms. Philadelphia, PA: Society for Industrial and Applied Mathematics.
[10] Muckley, M.J., Riemenschneider, B., Radmanesh, A., Kim, S., Jeong, G., Ko, J., … Knoll, F. (2021). Results of the 2020 fastMRI challenge for machine learning MR image reconstruction. IEEE Trans. Med. Imaging, 40(9), 2306-2317.
[11] Smale, S. (1998). Mathematical problems for the next century. Math. Intell., 20, 7-15.
[12] Turing, A.M. (1937). On computable numbers, with an application to the Entscheidungsproblem. Proc. London Math. Soc., s2-42(1), 230-265.