Pseudomagnetism in Photonics: From Mathematical Theory to Experiment

While magnetic fields deflect the paths of charged particles like electrons, they do not directly influence the path of light. In 2021, we developed a mathematical theory that demonstrated how to engineer a two-dimensional (2D) nonmagnetic photonic crystal in which photons of light move much like electrons under the influence of a magnetic field [5]. In particular, we showed that a nonuniformly deformed photonic (or other wave-propagating) continuous 2D medium with honeycomb spatial symmetries gives rise to effective pseudomagnetic and electric fields, which influence the propagation of light waves. A strained pattern that produces a constant perpendicular pseudomagnetic field induces photonic Landau levels within the structure. We can use these infinitely degenerate states of light to enhance light-matter interactions; potential applications include increased emission from quantum emitters such as quantum dots, and more efficient generation of quantum light in the form of entangled pairs of photons. Our study also suggested strategies for inducing topological phenomena in photonic and other wave systems that are analogous to the phenomena in quantum materials. Recent experiments observed and confirmed our predictions [1, 2]. 

Our work was motivated by an analogous effect in condensed matter physics for the 2D material graphene: a monolayer of carbon atoms with the symmetries of a honeycomb tiling. After graphene’s discovery, researchers realized that appropriately strained graphene causes electrons to behave as though they were flowing in the presence of an out-of-plane magnetic field — thus exhibiting Landau-level electronic spectra with a high density of electronic states [9].

Is such an effect possible for photons as well? A previous study used the tight-binding approximation, which underlies condensed matter predictions for graphene, to anticipate this effect for photons in optical waveguide arrays [10]. However, tight-binding theory is not valid in 2D photonic crystals [6]; instead, we proposed a continuum theory that is applicable to 2D Maxwell’s equations [5]. As a complement to our experimental work [2], we extended this theory to encompass the vectorial effects of three-dimensional Maxwell’s equations. This vectorial theory yields excellent agreement with experiment, with no free fitting parameters.

The Unstrained Honeycomb Medium and Dirac Quasi-particles

Time-harmonic transverse electric modes of Maxwell’s equations, which model electromagnetic waves of frequency \(\omega\) in a dielectric medium, are determined by solutions of the scalar Helmholtz equation

\[H\psi = -\nabla_x\cdot \xi(x)\nabla_x\  \psi(x) = E\psi(x),\quad x\in\mathbb R^2;\ E=\left(\frac{\omega}{c}\right)^2.\]

Here, \(\xi(x)= [\varepsilon(x)]^{-1}\) and \(\varepsilon(x)\) denotes the medium’s electric permittivity. We assume that the medium is nonmagnetic and set the vacuum value for the magnetic permeability as \(\mu=\mu_0\). The scalar function \(\psi(x)=\psi(x_1,x_2)\) denotes the \(x_3\) (longitudinal) component of the magnetic field: \(\mathbf{H}(x) = \psi(x) \hat{\mathbf{x}}_3\). We also assume that the dielectric constant has the symmetries of honeycomb tiling on the plane (see Figure 1a). Precisely, we suppose that \(\xi(x)\) is periodic with respect to the equilateral triangular lattice, invariant under parity inversion \((\mathcal{P}[\xi](x)=\xi(-x)=\xi(x))\), and real-valued \((\mathcal{C}[\xi](x)=\overline{\xi(x)}=\xi(x))\).

Since \(L=-\nabla_x\cdot \xi(x)\nabla_x\) is a self-adjoint operator on \(L^2(\mathbb R^2)\) with periodic coefficients, \(L\) has a Floquet-Bloch band structure: a generalization of the usual spectral decomposition of \(L^2(\mathbb R^2)\) into the plane-wave eigenstates of the Laplacian that arise for \(\xi(x)\equiv 1\). We can express the wave propagation in a honeycomb medium via a continuous weighted superposition of Floquet-Bloch modes \(\Phi(x,k)\in L^2_{\rm loc}\) that solve the family of self-adjoint elliptic eigenvalue problems

\[H\Phi=\ E \Phi,\quad \Phi(x+v,k)= e^{ik\cdot v}\Phi(x,k), \tag1\]

which are parameterized by the quasi-momentum (or \(k\) pseudo-periodicity parameter) \(k\in\mathcal{B}\). Here, \(\mathcal{B}\) is the Brillouin zone: a fundamental period cell that is associated with the dual lattice \(\Lambda^*\). For each \(k\in\mathcal{B}\), \((1)\) has a discrete spectrum of \(E_1(k)\le E_2(k)\le\dots\le E_b(k)\le\dots\) with corresponding \(k\) pseudo-periodic eigenstates \(\Phi_b(x,k)\) of \((1)\). The graphs \(k\mapsto E_b(k)\) are called dispersion surfaces or bands and are the analogues of dispersion relations that arise in the solution of constant coefficient wave equations via the Fourier transform.

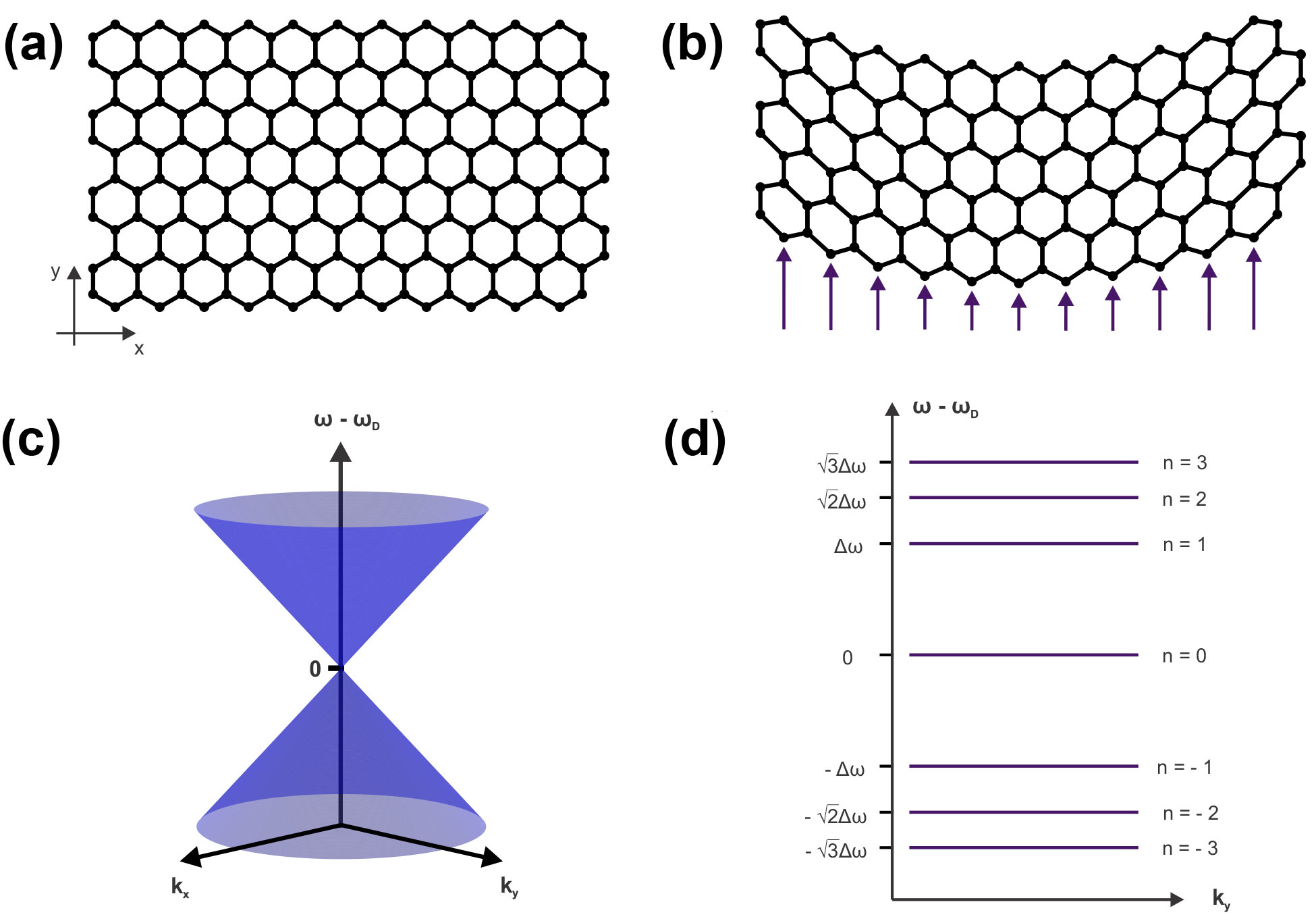
Remarkably, the symmetries of honeycomb media give rise to Dirac points in the band structure. At these energy/quasi-momentum pairs \((E_D,k_D)\), two adjacent dispersion surfaces touch in a locally conical manner:

\[\begin{eqnarray} &E_\pm&(k)-E_D \\ &=& \pm v_{D} | k -k_D|(\ 1 + \mathcal{O}(| k -k_D|)), \end{eqnarray}\]

where \(v_{D}>0\) and \(E_D=(\omega_D/c)^2\) [3, 8]. Figure 1a illustrates a medium with honeycomb symmetry, while Figure 1c depicts the local behavior of two dispersion surfaces that touch in a Dirac point. Around \(E=E_D\), the spectrum of \(H\) is continuous with zero density of states at \(E_D\). An important consequence of this local band structure—which underlies many of graphene’s important properties—is the fact that the envelope of wavepackets (quasi-particles) that are spectrally localized about a Dirac point propagates according to a system of 2D Dirac equations with propagation speed (Dirac/Fermi velocity) \(v_{D}\). The effective Dirac Hamiltonian is as follows [4]:

\[\cancel{D}_{{\rm eff}}\ \equiv v_{D}\ \sigma\cdot \mathbf{P}.\]

Here, \(\mathbf{P}= (-i\partial_{Y_1},-i\partial_{Y_2})\), \(\sigma_0={\rm Id}_{2\times2}\), \(\sigma=(\sigma_1,\sigma_2)\), and \(\sigma_j\) are the standard \(2\times2\) Pauli matrices.

Inducing Effective Magnetic and Electric Field Potentials

Now imagine a nonuniform distortion of the honeycomb medium (a strain) on a length scale of \(\kappa^{-1}\), which is large when compared with the triangular lattice period \(a\): \(x\mapsto T_\kappa(x)= x+ \mathbf{u}(\kappa x)\), where \(\kappa a\ll1\). Figure 1b displays a strain deformation that only varies along \(x_1\); it maintains discrete translation symmetry with respect to \(x_2\). The modes of the strained medium are governed by the deformed Helmholtz equation

\[-\nabla_x\cdot\xi^\prime(x)\nabla_x\  \psi(x) = \left(\frac{\omega}{c}\right)^2 \psi(x),\quad x\in\mathbb R^2,\]

with dielectric parameter \(\xi^\prime(x)=(\xi\circ T_\kappa^{-1})(x)\), where \(\xi(x)=1/\varepsilon(x)\).

So, how do wavepackets evolve in such a distorted medium? We found that the envelope of wavepackets evolves under \(i\partial_T\alpha = \cancel{D}_{A,{\rm eff}} \alpha\): a Dirac equation where

\[\cancel{D}_{A,{\textrm {eff}}} \equiv v_{D} \ \sigma\cdot (\mathbf{P}-\mathbf{A}_{\textrm{eff}}) + \sigma_0 W_{\textrm {eff}}.\]

\(\mathbf{A}_{\textrm{eff}}(\mathbf{Y})\) and \(W_{\textrm{eff}}(\mathbf{Y})\) are effective magnetic and electric potentials that are given explicitly in terms of the deformation \(x\mapsto T_\kappa(x)\) [5].

Choice of Strain Gives Rise to Photonic Landau Levels

Next, we describe the connection between the choice of strain and the scenario in Figures 1b and 1d. For a strain with a single direction of discrete translation symmetry (as in Figures 1b and 1d), the band structure consists of dispersion curves that are parameterized by a single quasi-momentum parameter \(k_y\). If this distortion is taken to be quadratic—that is, \(T_\kappa(x) = (x_1,x_2) + ( 0, (\kappa x_1)^2 )\)—then we claim that for small \(\kappa\), the dispersion curves are well-approximated in an asymptotic sense by the flat \(k_y\) independent bands (see Figure 1d). The eigenspaces that correspond to the flat bands are spanned by states of the form \(g(x_1)e^{ik_y x_2}\), which are Gaussian localized in the \(x_1\) direction (around the structure’s center of symmetry) and similar to plane waves in the \(x_2\) direction. Because the group velocity vanishes on a flat band, wavepackets that are formed from a superposition of these states will neither transport nor dispersively spread light. Such states are therefore candidates for enhanced light-matter coupling, including nonlinear optical effects.

Experiments

We used a silicon-on-insulator platform to conduct our experiments and employed electron beam lithography to fabricate a periodic photonic crystal by etching small triangles into a silicon slab—220 nanometers thick with a refractive index of 3.5—on a silica substrate with a refractive index of 1.5 (see Figure 2). The periodic structure is a honeycomb lattice with six-fold rotational symmetry. Experimentally, we injected a focused beam (several microns in width) onto the slab and captured the reflected light through the focusing lens. The slab’s band structure corresponds to resonant modes at particular wave vectors \(\mathbf{k}\) and frequencies \(\omega\) that absorb the incoming light and produce clearly observable features in the reflectance spectra at the appropriate angles and wavelengths.

We fabricated this structure in both the fully periodic honeycomb lattice geometry and the strained geometry, wherein the lattice is distorted according to the transformation \(T_\kappa\) (described above). In the periodic case, the Dirac cone is associated with the six-fold rotational symmetry of the structure. And in the strained geometry, the spectra did indeed break into Landau levels, reflecting the pseudomagnetic field that resulted from the strain. The spacing between Landau levels closely matched predictions from our theoretical description based on a two-scale expansion [2, 5] (see Figure 2).

In practice, the Landau levels are not perfectly flat. Some dispersion exists in \(k_2\) because the strain locally shifts the frequency of the Dirac cone up and down — a phenomenon that does not arise in the tight-binding model for solid-state graphene. We subsequently found that we could mitigate this dispersion and flatten the Landau level bands by adding an additional strain with a different functional form, namely \(T_\kappa(x) = (x_1,x_2) + (0, (\kappa x_1)^2) + ( (\beta x_1)^3, 0 )\). This strain induces an additional pseudoelectric potential and locally shifts the Dirac cone’s frequency in the opposite direction, effectively flattening the Landau levels (see Figure 3).

Concluding Remarks and Future Work

Since their very conception [7, 11], photonic crystals have been used to engineer the density of states — either decreasing it in a band gap to suppress emission or increasing it to achieve stronger light-matter coupling. Periodicity-breaking strains offer a new design principle to engineer photonic crystals and improve their properties. This capability can find purpose in a variety of applications, including the design of lower-threshold on-chip lasers; the shaping of the spectral and spatial profiles of these lasers’ modes; the realization of enhanced nonlinear optical effects, such as photon pair generation; and strong coupling to quantum emitters. Ultimately, the use of gauge fields to mathematically describe the effects of aperiodic photonic crystals will facilitate a better analytical understanding of the effects of deformation without resorting to brute-force numerics. This form of physical intuition will likely enable the design of new structures whose relevant physical properties bridge very distinct length scales.

Acknowledgments: We gratefully acknowledge funding from the Office of Naval Research’s Multidisciplinary University Research Initiatives (MURI) program under agreement N00014-20-1-2325, the Air Force Office of Scientific Research’s MURI program under agreement FA9550-22-1-0339, the Ewing Marion Kaufman Foundation under grant KA2020-114794, and the David and Lucile Packard Foundation under grant 2017-66821. This research was also supported in part by National Science Foundation grants DMS-1620422, DMS-1620418, DMS-1908657, and DMS-1937254, as well as the Simons Foundation’s Math+X Investigator Award #376319.

References
[1] Barczyk, R., Kuipers, L., & Verhagen, E. (2024). Observation of Landau levels and chiral edge states in photonic crystals through pseudomagnetic fields induced by synthetic strain. Nat. Photon., 18(6), 574-579. 
[2] Barsukova, M., Grisé, F., Zhang, Z., Vaidya, S., Guglielmon, J., Weinstein, M.I., … Rechtsman, M.C. (2024). Direct observation of Landau levels in silicon photonic crystals. Nat. Photon., 18, 580-585.
[3] Fefferman, C.L., & Weinstein, M.I. (2012). Honeycomb lattice potentials and Dirac points. J. Am. Math. Soc., 25(4), 1169-1220.
[4] Fefferman, C.L., & Weinstein, M.I. (2014). Wave packets in honeycomb lattice structures and two-dimensional Dirac equations. Commun. Math. Phys., 326, 251-286.
[5] Guglielmon, J., Rechtsman, M.C., & Weinstein, M.I. (2021). Landau levels in strained two-dimensional photonic crystals. Phys. Rev. A, 103(1), 013505.
[6] Joannopoulos, J.D., Villeneuve, P.R., & Fan, S. (1997). Photonic crystals. Solid State Commun., 102(2-3), 165-173.
[7] John, S. (1987). Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett., 58(23), 2486-2489.
[8] Lee-Thorp, J.P., Weinstein, M.I., & Zhu, Y. (2018). Elliptic operators with honeycomb symmetry: Dirac points, edge states and applications to photonic graphene. Arch. Ration. Mech. Anal., 232, 1-63.
[9] Novoselov, K.S., Geim, A.K., Morozov, S.V., Jiang, D., Katsnelson, M.I., Grigorieva, I.V., … Firsov, A.A. (2005). Two-dimensional gas of massless Dirac fermions in graphene. Nature, 438(7065), 197-200.
[10] Rechtsman, M.C., Zeuner, J.M., Tünnermann, A., Nolte, S., Segev, M., & Szameit, A. (2013). Strain-induced pseudomagnetic field and photonic Landau levels in dielectric structures. Nat. Photon., 7(2), 153-158. 
[11] Yablonovitch, E. (1987). Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett., 58(20), 2059-2062.