Randomization in Characterizing the Subsurface

Current methods for characterizing Earth’s subsurface, such as standard inverse techniques, are not sufficiently accurate to meet the needs of modern applications in the fields of energy exploration, environmental management, and global security. While increasing the quantity of field measurements and robustness of the applied data-/model-analysis methods can improve accuracy, such approaches can be computationally impractical for large data sets and complex site conditions. Therefore, there is a need to develop economically-feasible and robust computational methods while maintaining accuracy. For example, in-field drilling for geothermal operations may yield high failure rates, resulting in unacceptably high costs; errors and/or large uncertainties in the estimated subsurface characteristics are the main impediment to the successful siting of an in-field well. This problem is not uniquely geothermal. Accurate characterization of uncertain subsurface properties is also critical for monitoring storage of carbon dioxide, estimating pathways of subsurface contaminant transport, and supervising ground-based nuclear-explosion tests.

We have developed various methods to characterize the subsurface, including efficient computational strategies to identify subsurface permeability given a set of hydraulic heads, as shown in Figure 1, and a data-driven subsurface geological feature detection approach using seismic measurements, as shown in Figure 2. A major challenge for many subsurface applications is the large number of observations and high feature dimensionality.

Randomized matrix algorithms—which aim to construct a low-rank approximation of an input matrix—have received a great deal of attention in recent years. The low-rank approximation, often called a matrix “sketch,” is usually the product of two smaller matrices, which yields a good approximation that represents the original output’s essential information. Therefore, one can employ a sketching system as a surrogate for the original data to compute quantities of interest. We have employed randomization techniques to solve various large-scale computational problems. Here we provide examples to demonstrate two major applications in solving real-world subsurface problems.

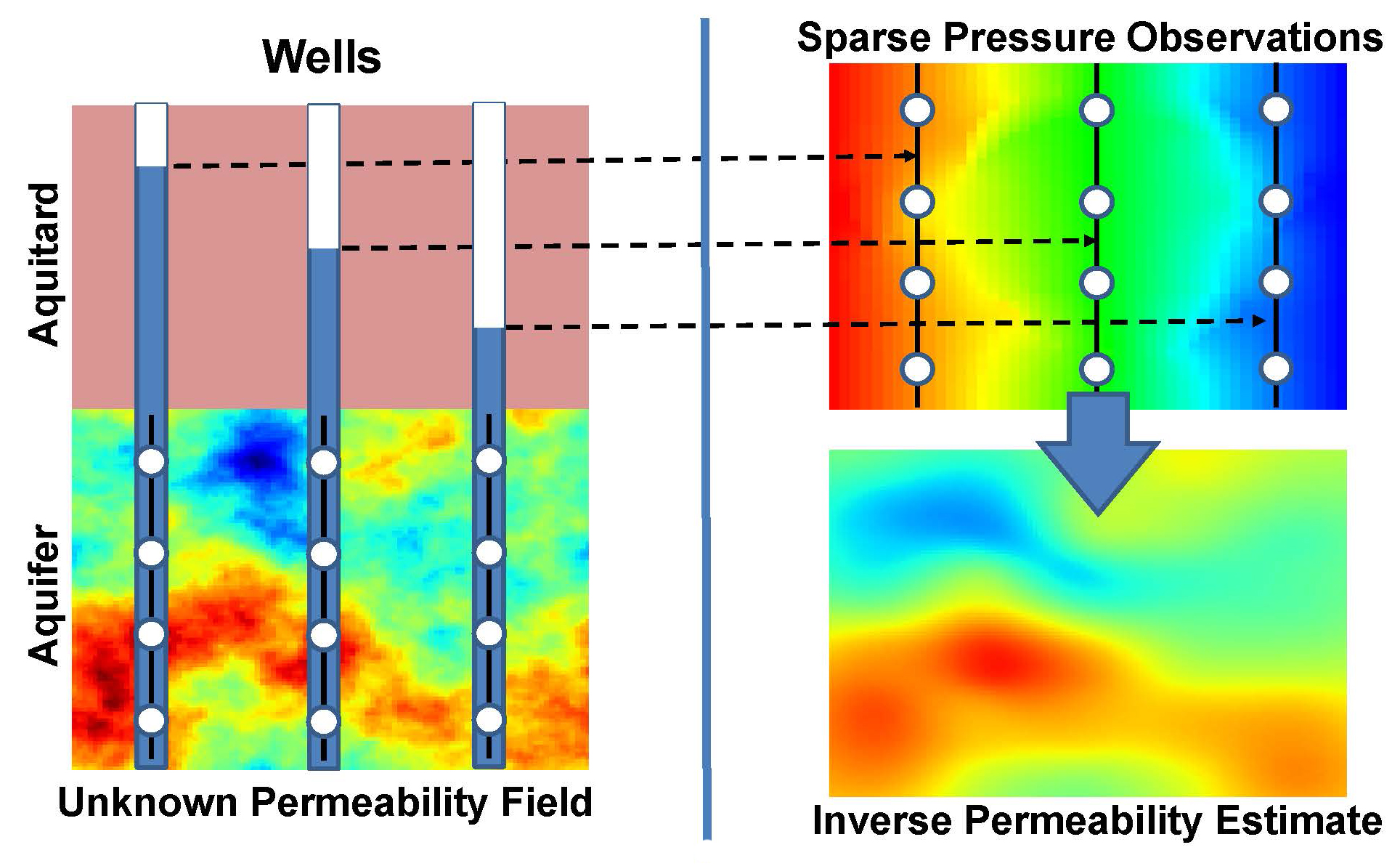
Randomized Subsurface Permeability Estimation

A porous medium’s permeability is a physical quantity needed to predict flow and transport of fluids and contaminants in the subsurface. The permeability’s estimation is often posed as a regularized inverse problem

$$\begin{array}{}\text{(1)}& \stackrel{\mathbf{~}}{\mathbf{x}}=argmi{n}_{\mathbf{x}}\{\parallel \mathbf{d}-f(\mathbf{x}){\parallel }_R^2+\lambda \parallel \mathbf{x}-X\beta {\parallel }_Q^2\},\end{array}$$

where $f$ is the forward operator mapping from the permeability to the pressure (called “hydraulic head” in hydrology parlance), $\mathbf{d}$ is a recorded hydraulic head dataset, $\mathbf{x}$ is a vector of permeabilities, $\parallel \mathbf{d}-f(\mathbf{x}){\parallel }_R^2$ measures the data misfit, and $\parallel \mathbf{x}-X\beta {\parallel }_Q^2$ is the regularization term.

The solution to $(1)$ can be obtained as

$$\begin{array}{}\text{(2)}& \stackrel{\mathbf{~}}{\mathbf{x}}=X\beta +Q{H}^T\epsilon ,\end{array}$$

where $H$ is the Jacobian matrix of the forward modeling operator $f$, defined as

$$\begin{array}{}\text{(3)}& H=\frac{\partial f}{\partial \mathbf{x}}{\mid }_{\mathbf{x}=\overline{\mathbf{x}}}.\end{array}$$

One may obtain $\beta$ and $\epsilon$ by solving the linear system

$$\begin{array}{}\text{(4)}& (\genfrac{}{}{0ex}{}{HQ{H}^T+RHX}{(HX{)}^{T}0})(\genfrac{}{}{0ex}{}{\epsilon }{\beta })=(\genfrac{}{}{0ex}{}{\mathbf{y}-f(\overline{\mathbf{x}})+H\mathbf{x}}{0}).\end{array}$$

However, solving $(4)$ can be both prohibitively expensive and memory demanding. To combat this problem, we developed a novel randomized technique that enables an efficient computational method [1].

Our approach aims to construct a sketching matrix, the elements of which are drawn randomly from a Gaussian distribution. We then replace the data $\mathbf{d}$ with $S\mathbf{d}$ and the forward $f(\mathbf{x})$ with $Sf(\mathbf{x})$. Therefore, the linear system in $(2)$ and $(4)$ can be substituted correspondingly with

$$\begin{array}{}\text{(5)}& \hat{\mathbf{x}}=X\beta +Q{H}^T{S}^T\epsilon \end{array}$$

and

$$\begin{array}{}\text{(6)}& (\genfrac{}{}{0ex}{}{SHQ{H}^T{S}^T+RSHX}{(SHX{)}^{T}0})(\genfrac{}{}{0ex}{}{\epsilon }{\beta })=(\genfrac{}{}{0ex}{}{S(\mathbf{y}-f(\overline{\mathbf{x}})+H\overline{\mathbf{x}})}{0}).\end{array}$$

$(2)$ and $(5)$ and $(4)$ and $(6)$ seem almost identical, except for the introduction of matrix $S$. However, a simple computational cost analysis can reveal the significant impacts of the randomized matrix. Assume that the number of model parameters is $\tilde{m}$; the number of observations is $\tilde{n}$, which yields the size of the Jacobian matrix $H\in {\mathbb{R}}^{\tilde{n}\times \tilde{m}};$ and the covariance matrix is $Q\in {\mathbb{R}}^{\tilde{n}\times \tilde{m}}$. We also denote the rank of the sketching matrix by $k$, and $k\ll \tilde{n}$. The drift matrix $X\in {\mathbb{R}}^{\tilde{m}\times \tilde{p}}$, where $\tilde{p}$ is small. The dimension of the original system matrix in $(4)$ is $((\tilde{n}+p)\times (\tilde{n}+p))$, while the dimension of the randomized system in $(6)$ is $((k+p)\times (k+p))$ — much smaller than the original system. Therefore, the computational cost of solving $(6)$ is significantly lower than that of solving $(4)$; this is the power of randomization in solving traditional inverse problems, as illustrated in [1]. The developed methods are available in the open source code Mads.

Subsurface Geological Feature Detection Using Randomized Data-Driven Methods

Seismic waves are more sensitive to the acoustic/elastic impedance of the subsurface than other geophysical measurements (see Figure 2). Hence, seismic exploration has been widely used to infer heterogeneities in media impedance, which indicate geologic structures.

Analyzing and interpreting seismic measurements for identifying prospective geological features is challenging. The difficulties arise from the processing of large amounts of seismic data and the incorporation of subjective human factors. Different geologic features play different roles in characterizing subsurface structure. In particular, identifying geological fault zones is essential to many subsurface energy applications. In carbon sequestration, potential leaks of stored carbon dioxide can create geologic faults, so knowing fault locations is necessary to monitor carbon dioxide storage. We have developed a novel data-driven geological feature detection method and successfully applied it to seismic measurements [2, 3], as illustrated in Figure 2. Both historical and simulated seismic data are fed into learning algorithms. A detection function $f\ast (\mathbf{x})$ is the output of the training process, where $\mathbf{x}$ represents the pre-stack seismic measurements. The function creates a link from the seismic measurements to the corresponding geological features.

Suppose one has $n$ historical feature vectors $\mathbf{X}={[{\mathbf{x}}_{\mathbf{1}}^{\mathbf{T}}\cdots {\mathbf{x}}_{\mathbf{n}}^{\mathbf{T}}]}^{\mathbf{T}}\in {\mathbb{R}}^{n\times d}$, which are from seismic measurements and ${\mathbf{x}}_i\in {\mathbb{R}}^d$, and the associated labels $\mathbf{y}=[y_1\cdots y_n{]}^T\in {\mathbb{R}}^{n\times 1},$ which in this example denote the location of the dipping angle of geologic faults. The kernel ridge regression (KRR) is utilized to learn the mapping function [2, 3]. We directly state the dual problem of KRR without derivation

$$\begin{array}{}\text{(7)}& \alpha =argmi{n}_{\alpha }\{\frac{1}{2}{\mathrm{\Sigma }}_{i=1}^n\parallel y_i-(K\alpha {)}_i{\parallel }_2^2+\frac{\lambda }{2}{\alpha }^{T}K\alpha \},\end{array}$$

where $K$ is a kernel function and $\lambda >0$ is a regularization parameter. The problem in $(7)$ has a closed-form solution 

$$\begin{array}{}\text{(8)}& {\alpha }^{\star }=(K+\lambda I_n{)}^{-1}\mathbf{y}\in {\mathbb{R}}^{\mathbf{\text{n}}},\end{array}$$

where $I_n$ is a $n\times n$ identity matrix. Finally, for any unknown data ${\mathbf{x}}^{\prime }\in {\mathbb{R}}^d$, the prediction made by KRR can be obtained by

$$\begin{array}{}\text{(9)}& f(\mathbf{x}\prime )={\mathrm{\Sigma }}_{i=1}^n{\alpha }_i^{\star }\kappa ({\mathbf{x}}^{\prime },{\mathbf{x}}_i).\end{array}$$

However, the direct utilization KRR prediction in $(7)$ is computationally expensive, because of the inversion of the large-scale matrix in $(8)$. We employ the Nyström method—a randomized kernel matrix approximation tool—to the geologic detection task, aiming to solve large-scale problems using modest computational resources.

The Nyström method computes a low-rank approximation $K\approx \psi {\psi }^T$ in $\mathcal{O}(nds+n{s}^2)$ time. Here, $s\ll n$ is user-specified; larger values of $s$ lead to better approximation but incur higher computational costs. We can compute the tall-and-skinny matrix $\psi \in {\mathbb{R}}^{n\times s}$ as follows. First, we sample $s$ items from $\{1,\cdots ,n\}$ uniformly at random without replacement; let the resulting set be $\mathcal{S}$. Subsequently, we construct a matrix $C\in {\mathbb{R}}^{n\times s}$ as $c_{il}=\kappa ({\mathbf{x}}_i,{\mathbf{x}}_l)$ for $i\in \{1,\cdots ,n\}$ and $l\in \mathcal{S}$;  let  $W\in {\mathbb{R}}^{s\times s}$ contain the rows of $C$ indexed by $\mathcal{S}$. Figure 3 illustrates the approximation. Finally, we compute the low-rank approximation $\psi =C(W^{†}{)}^{1/2}$.

With the low-rank approximation obtained via the Nyström method, we can efficiently calculate an approximated solution

$$\begin{gathered} \begin{array}{}\text{(10)}& \tilde{\alpha }=\psi {\psi }^T+\lambda I_n{)}^{-1}\mathbf{y}, \\ ={\lambda }^{-1}\mathbf{y}-{\lambda }^{-1}\psi (\lambda I_s+{\psi }^T\psi {)}^{-1}{\psi }^T\mathbf{y},\end{array} \end{gathered}$$

where the latter equality follows from the Sherman-Morrison-Woodbury matrix identity. It is worthwhile mentioning that the $n\times n$ matrix of $\psi {\psi }^T$ in $(8)$ has been replaced by the matrix of ${\psi }^T\psi \in {\mathbb{R}}^{s\times s}$, which is much smaller. This significantly reduces the computational costs. More details and results can be found in [2, 3].

Acknowledgements: This work was co-funded by the U.S. Department of Energy (DOE) Office of Fossil Energy’s Carbon Storage program, Los Alamos National Laboratory Environmental Programs, and the DOE Office of Science (DiaMonD project: An Integrated Multifaceted Approach to Mathematics at the Interfaces of Data, Models, and Decisions, Grant #11145687).

References

[1] Lin, Y., Le, E., O’Malley, D., Vesselinov, V., & Bui-Thanh, T. (2017). Large-Scale Inverse Model Analyses Employing Fast Randomized Data Reduction. Wat. Resc. Res, 53(8), 6784-6801.
[2] Lin, Y., Wang, S., Thiagarajan, J., Guthrie, G., & Coblentz, D. (2017). Efficient Data-Driven Geologic Feature Detection from Pre-stack Seismic Measurements using Randomized Machine-Learning Algorithm. Preprint, arXiv:1710.04329.
[3] Lin, Y., Wang, S., Thiagarajan, J., Guthrie, G., & Coblentz, D. (2017). Towards Real-Time Geologic Feature Detection from Seismic Measurements using a Randomized Machine-Learning Algorithm. In SEG Technical Program Expanded Abstracts 2017 (pp. 2143-2148). Houston, TX: Society of Exploration Geophysics.