Rapid Prototyping with Julia: From Mathematics to Fast Code

Software development—a dominant expenditure for scientific projects—is often limited by technical programming challenges, not mathematical insight. Here we share our experience with the Julia programming language in the context of the U.S. Department of Energy’s Exascale Computing Project (ECP) as part of ExaSGD, a power grid optimization application. Julia is a free and open-source language that has the potential for C-like performance while extending the expressivity of MATLAB [5]. It is meant for scientific computing and has helped us effectively collaborate as a team of mathematicians and software engineers. Our ratio of mathematical reasoning to software development tasks has vastly improved as a result, empowering us to do more mathematics per unit of code.

ECP is an aggressive research, development, and deployment project that focuses on the delivery of mission-critical applications, an integrated software stack, and exascale hardware technology advances. It partners with leadership computing facilities at the Department of Energy, including Oak Ridge Leadership Computing Facility and Argonne Leadership Computing Facility. These facilities employ heterogeneous architectures that feature graphics processing units (GPUs) in their recent and imminent exascale-barrier-breaking systems, Frontier and Aurora. 

We opted to use Julia in our work to handle the complexity of GPUs: hardware accelerators that are crucial for ECP’s ambitious goals yet increasingly available as commodity hardware for scientists. The appearance of GPUs obliterated our original optimization algorithm plans for ECP; our algorithms relied on direct sparse indefinite linear solvers, which had little to no support on GPUs for our use case at the time. We thus found ourselves needing to redesign and reimplement many of our core functions — a process that allowed us to contemplate radically different approaches.

Before GPUs entered the scene, we utilized Julia’s algebraic modeling package JuMP as a modeling language [3]. We quickly realized that portability and modeling are two sides of the same coin, and found Julia to be a fast tool for prototyping novel optimization algorithms and models on GPUs. We developed and published various packages in a timeframe that would have been unimaginable for our team’s previous projects. 

As a result of Julia’s built-in features, our packages are now available to a wider audience and follow best practices in software engineering, such as unit testing and documentation. They are also capable of running on any machine, from laptops to supercomputers like Summit at Oak Ridge National Laboratory. We recently shared our adventure diary in an article for the SIAM Activity Group on Optimization that details a possible generic template for how Julia might help implement newly-developed mathematical methods for a plethora of high-performance computing architectures in record time [1].

Now we will describe the core features of Julia that enable fast pathways from mathematics to applications in a nearly hardware-agnostic fashion.

Symbolic Calculus and Metaprogramming

Calculus represents the core of numerical algorithms. It is largely restricted to function compositions \(g \circ f\) in mathematics, which directly map to function compositions in programming. However, these functions are a black box after compilation; \(f\) and \(g\) become input-output functions, and their expressions are lost at runtime. For example, the application of symbolic derivative calculus to a function \(f\) becomes difficult to implement. Metaprogramming precisely addresses this lack of access to the expressions of \(f\) and \(g\). This programming technique allows a program A to take another program B’s expressions as an input (instead of B’s output), then semantically transforms program B into new expressions for program C. As such, interfaces are not reduced to mere exchanges of data. Instead, they acquire an emergent property of creating a program C through expression transformation of program A (transformer) on program B (transformed):

mul(a,b) = a\(\ast\)b
\(\nabla\)mul(a,da,b,db) = (a\(\ast\)b), (a\(\ast\)db + da\(\ast\)b) 

For instance, program mul that implements a\(\ast\)b transforms into program \(\nabla\)mul that implements its derivative via an automatic differentiation tool. Recently, the “differentiable programming” technique emerged to describe the capability of such a differentiation workflow. Similarly, more complex expression transformations appear in uncertainty quantification, differential equations, performance profiling, and debugging — nearly everywhere in scientific computing.

These expression transformations often hijack programming language features like operator overloading and C++ templates, or they are compiler integrated. We believe that three of Julia’s design features make it uniquely positioned to tackle such classes of metaprogramming problems:

• Macros (functions over expressions)
• Multiple dispatch and specialization
• Just-in-time (JIT) compilation through the LLVM compiler.

Consequently, the process from compilation to a binary and eventually an executable is no longer sequential. The compilation and execution steps are intertwined, thus making compilation a part of the runtime. This dynamic compilation is both Julia’s biggest strength and one of its weaknesses. LLVM’s original design did not support a JIT language, so the time-to-first-plot is an ongoing challenge in Julia. To reduce the compilation time, users must be aware of both type stability and the language’s various intricacies. Ongoing work focuses on caching compiled code and making this issue more transparent and user-friendly.

On the upside, macros enable the manipulation of expressions; multiple dispatch allows an algorithm to apply other algorithms based on their type, then specialize upon the inputs; and JIT compilation creates optimized programs that can take advantage of modern hardware. Instead of addressing each feature from a theoretical perspective, we illustrate the way in which they jointly facilitate a compact and transparent code that remains portable and differentiable.

Portability and Differentiability

As an example, we implement the function speelpenning \(y = \prod_{i= 1}^{n} x_i\) [6]:

speelpenning(x) = reduce(\(\ast\),x)

This function is mapped to the Julia internal reduction reduce with the product operator \(\ast\). So far, x has no type. Initializing x to a vector of type T=Vector{Float64} yields the following:

x = [i/(1.0+i) for i in 1:n]       # Vector{Float64}
speelpenning(x)                     # 0.090909...

The function speelpenning is then dispatched on this type T, calling the appropriate and optimized reduction and culminating in the compiled binary machine code. We compute the gradient of speelpenning with Zygote, an automatic differentiation tool in Julia [4]:

using Zygote
g = speelpenning’(x)

The Zygote operator ‘’’ transforms speelpenning into its gradient computation via access to the LLVM intermediate representation and based on differentiation rules that are defined in the package ChainRules.jl. All of this code is only compiled once we call speelpenning’.

Suppose that we decide to run our code on a NVIDIA GPU. CUDA.jl—the package for writing CUDA kernels in Julia [2]—uses the broadcast operator ‘.’ to naturally vectorize statements like a .= b .+ c, where a, b, and c are vectors. The entire statement is effectively fused into one kernel, so let’s try to execute our differentiated speelpenning on a NVIDIA GPU. To do so, we move vector x onto the GPU via the CuArray constructor and call the gradient computation. The entire machinery now compiles the code with this new data type and dispatches onto the GPU. However, executing this code in its current state fails:

cux = CuArray(x)
cug = speelpenning’(cux)

Why does it fail? No differentiated function is defined for reduce(\(\ast\),x). A reduction is a nontrivial operation that is difficult to efficiently parallelize, but we now know that we can compute the gradient with \(\frac{\partial x_i}{\partial y} = y/x_i\) for \(x_i \neq 0\). Use of the broadcast operator allows for a nicely parallel implementation dx[i].= y ./ x[i]. Such custom derivatives are often necessary for differentiable programming, and their integration into the code requires detailed knowledge of the automatic differentiation tool internals. Assuming that our application’s domain excludes \(x=0\), how can we make Zygote aware of our insight? We define a custom differentiation rule for reduce and inject it into our code (see Figure 1).

With this special case for product reduction, we now have a 17-line, fast implementation of speelpenning on the GPU without ever interacting with the developers of CUDA.jl, Zyote.jl, or ChainRules.jl. Imagine the effort of doing this in a computing language that lacks macros and abstract syntax tree manipulation, multiple dispatch, or JIT compilation. These features allow us to implement the fully differentiable power flow solver ExaPF.jl that runs efficiently on both GPU and central processing unit architectures — all while providing first and second-order derivatives of the power flow. Still, a cautionary remark is appropriate. Because Julia is developing quickly, all of these features come with a certain fragility and incompleteness. Nevertheless, we are confident that we can achieve exascale with Julia on Aurora and Frontier.

Is It Fast?

Julia utilizes LLVM, a leading compiler backend for C/C++. In theory, it should permit Julia implementations to achieve C-like performance. However, LLVM also requires a considerable low-level understanding of the Julia language implementation. This balance of development cost versus performance is an ongoing debate in the scientific community. How desirable is a 2x speedup at 10 times the financial development cost? Julia enables an insightful preliminary performance assessment for novel algorithm implementations. Although not required, one can even create competitive BLAS implementations in pure Julia. 

ExaTron.jl solves the optimal power flow subproblem and is crucial for the performance of our ExaSGD software stack. Incidentally, we also implemented a C++/CUDA solution to compare performance (see Figure 2).

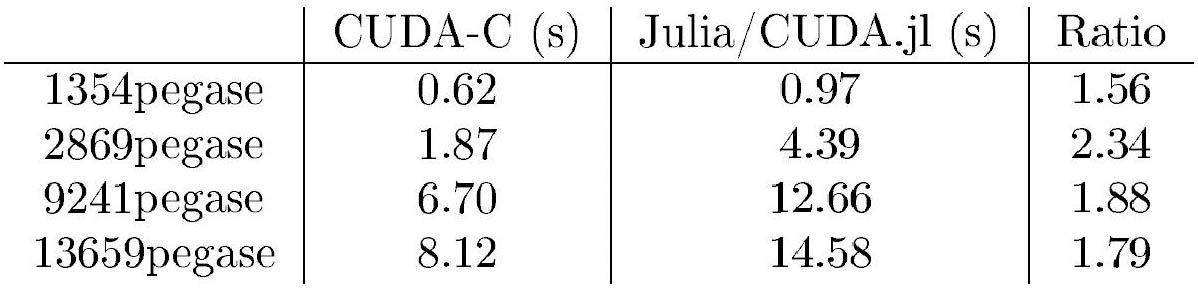
We do not claim that both versions of the code are fully optimized. But given the law of marginal gains, a Julia implementation requires much less effort to develop while simultaneously providing huge benefits for expression transformations like differentiable programming and portability.

References

[1] Anitescu, M., Maldonado, D.A., Pacaud, F., Kim, K., Kim, Y., Rao, V., … Subramanyam, A. (2021). Targeting exascale with Julia on GPUs for multiperiod optimization with scenario constraints. SIAG/OPT Views and News, 29(1), p. 1.
[2] Besard, T., Churavy, V., Edelman, A., & De Sutter, B. (2019). Rapid software prototyping for heterogeneous and distributed platforms. Adv. Engin. Soft., 132, 29-46.
[3] Dunning, I., Huchette, J., & Lubin, M. (2017). JuMP: A modeling language for mathematical optimization. SIAM Rev., 59(2), 295-320.
[4] Innes, M. (2018). Don’t unroll adjoint: Differentiating SSA-form programs. Preprint, arXiv:1810.07951.
[5] Perkel, J.M. (2019). Julia: Come for the syntax, stay for the speed. Nature, 572, 141-143.
[6] Speelpenning, B. (1980). Compiling fast partial derivatives of functions given by algorithms [Doctoral dissertation, University of Illinois at Urbana-Champaign]. U.S. Department of Energy Office of Scientific and Technical Information.