Red Sock Award at DS25 Recognizes Outstanding Student Research in Dynamical Systems

SIAM’s Red Sock Award acknowledges the best poster presentations by students and/or postdoctoral researchers at the biennial SIAM Conference on Applications of Dynamical Systems. As per tradition, each awardee receives a monetary prize of $100.00 and a pair of red socks in honor of James A. Yorke (University of Maryland, College Park), an influential figure in the dynamical systems community who is further distinguished by his signature crimson footwear.

The Red Sock Award became an official SIAM prize in 2013. At each dynamical systems conference, an ad hoc prize committee of judges anonymously visits all of the posters during the Poster Session and Dessert Reception, assigning individual scores to each presenter for their display and overall delivery. The judges use these scores to select the winners, who are then recognized publicly during the conference.

At the 2025 SIAM Conference on Applications of Dynamical Systems (DS25)—which took place in Denver, Colo., this past May—the DS25 ad hoc committee awarded the coveted prize to Twinkle Jaswal of Illinois State University, Juan Patiño-Echeverría of the University of Auckland, Laura Pinkney of the University of Leeds, and Anna Thomas of the University of Pittsburgh. Here, the 2025 recipients of the Red Sock Award provide brief overviews of their prizewinning work.

Photosensitivity and Neuronal Synchronization

Twinkle Jaswal, graduate student, Illinois State University

My DS25 poster focused on the use of computational modeling to study photosensitive seizures. I explored the possible effect of external stimuli—specifically, flashing lights in combination with elevated temperatures—on neuronal synchronization. Excessive neuron synchronization is present during epileptic seizures [5], and temperature might be an aggravating factor for individuals who are predisposed to photosensitive seizures. Elevated core body temperature can also impair cognition and increase seizure risk, negatively impacting brain function.

My collaborators and I developed a temperature-dependent neuronal network that consists of a \(15\times 15\) lattice of Hodgkin-Huxley-type model neurons [3], each of which is governed by a set of temperature-dependent differential equations. Bidirectional gap junctions connect the neurons, and synaptic coupling strength is modulated by an Arrhenius temperature scaling factor: \(\gamma(T)=4.0^{(T-T_0)/10}\). We used \(I_{\textrm{stim}}=A\sin(2\pi ft)\) to model visual stimulation, where \(A\) represents the stimulus amplitude, \(f\) denotes the frequency in hertz, and \(t\) is time in seconds. The uniform application of this stimulus to all neurons simulates the effect of rhythmic visual input that is transduced through the retina, influencing the entire network. We employed the Kuramoto order parameter \(R\) to measure synchronization across the network; a value of \(0\) indicates no synchronization, a value of \(1\) signifies complete synchronization, and values between \(0\) and \(1\) reflect partial synchronization.

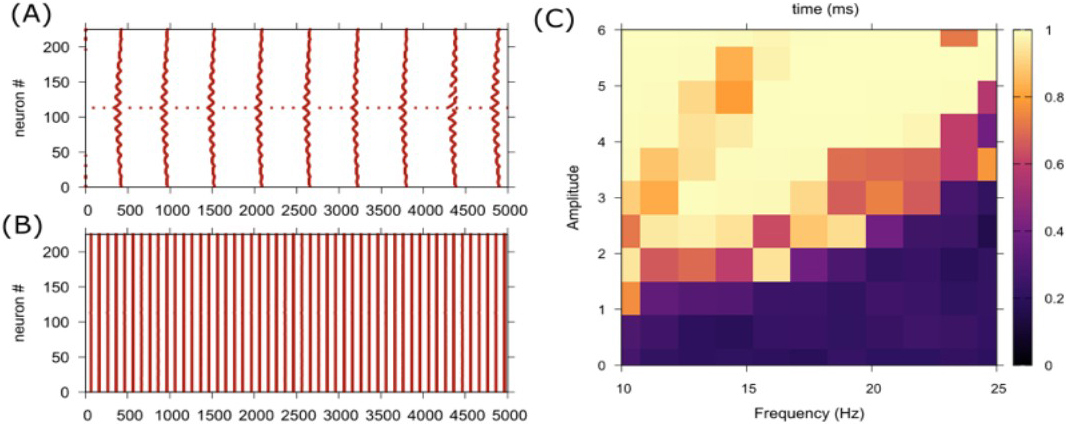
At the brain’s baseline temperature of 38° Celsius (C), our network reveals that flashing light alone can cause partial synchronization among neurons, even without synaptic connections (see Figure 1). This effect is especially noticeable in networks that are composed of neurons with similar firing properties. With the introduction of synaptic coupling, synchronization grows stronger and occurs across a wider range of visual stimulus amplitudes and frequencies.

To understand temperature’s influence on synchronization when combined with visual stimulation, we simulated the network at 36°C, 38°C, and 41°C. Results show that as temperature increases, the neurons become more synchronized — even at lower visual stimulus intensities. At higher temperatures, a wider range of visual stimulus amplitudes and frequencies can lead to synchronization. These findings suggest that elevated temperatures make the network more sensitive to external rhythmic input, amplify the effects of visual stimulation, and heighten the brain’s likelihood of entering a synchronized state.

Into the Wild: A Journey to Chaos in Four Dimensions

Juan Patiño-Echeverría, graduate student, University of Auckland

My DS25 poster shared new results on wild chaos, a higher-dimensional form of chaotic dynamics that only arises in vector fields with a dimension of four or higher. It is characterized by the persistent presence of tangencies between the stable and unstable manifolds of an invariant set [1]. My Ph.D. research focuses on a four-dimensional (4D) extension of the classic Lorenz system that is given by

\[\begin{cases}
\dot{x}=\sigma(y-x), \\
\dot{y}=x(\rho-z)-y, \\
\dot{z}=xy-\beta z + \mu w, \\
\dot{w}=-\mu z - \beta w,
\end{cases} \tag1\]

with fixed parameters \(\sigma=10\) and \(\beta={8/3}\). This system features the new parameter \(\mu\) and exhibits a wild pseudohyperbolic attractor for a specific choice of \(\rho\) and \(\mu\) [4].

Pseudohyperbolicity ensures that all trajectories in the attractor have a positive maximal Lyapunov exponent, and that this behavior is robust under perturbations. Our work seeks to understand the emergence of such a wild attractor when parameters change [8]. To that end, my colleagues and I explore the global bifurcation structure in the \((\rho,\mu)\)-parameter plane of system \((1)\). The crucial novel aspect is the existence of rotational dynamics near the origin in the \((z,w)\)-plane when \(\mu\) is “switched on.”

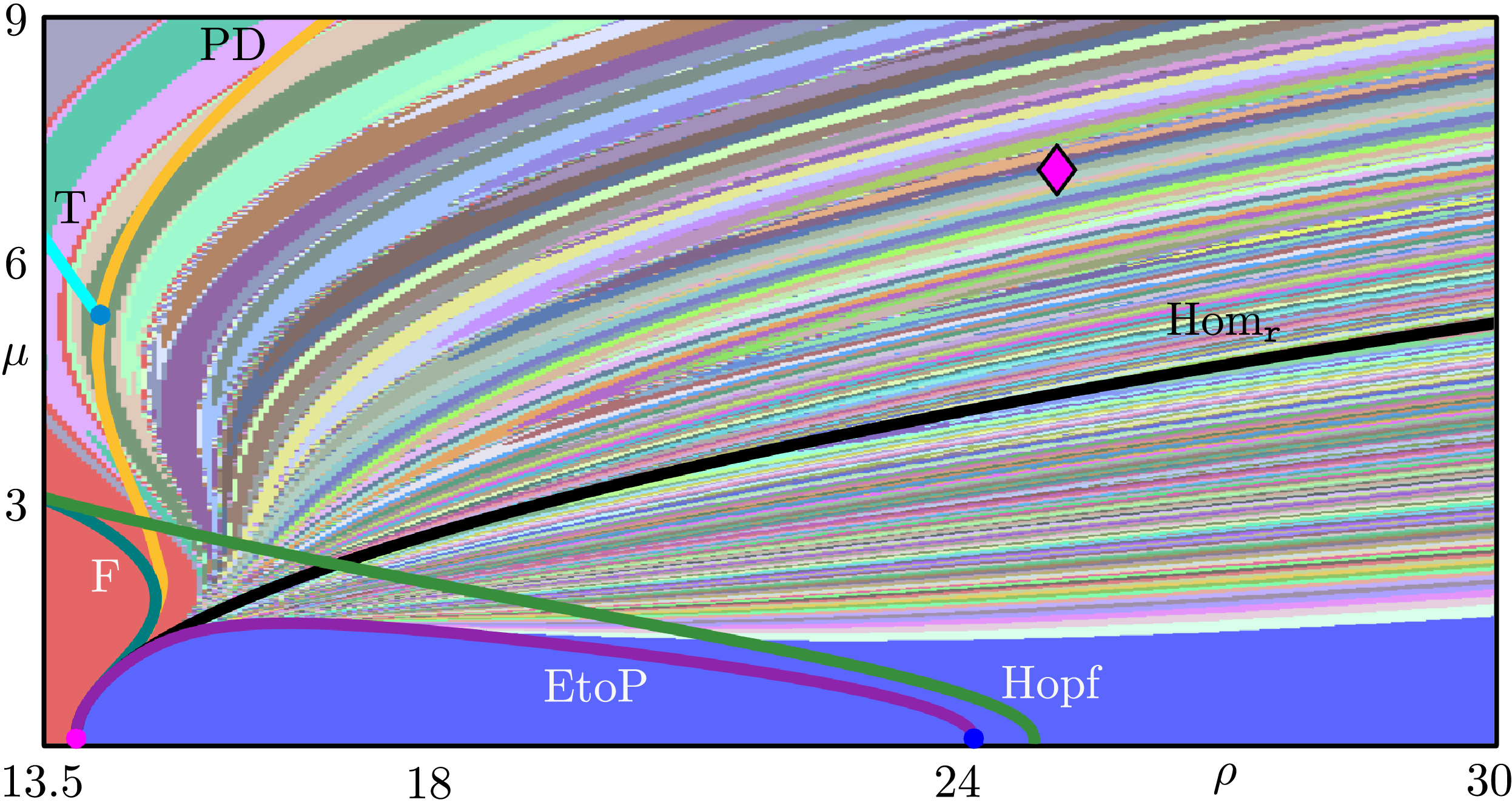
Our starting point is a bifurcation diagram with curves of homoclinic bifurcations and local bifurcations of equilibria and periodic orbits that are inherited from the Lorenz system when \(\mu=0\). We then found and continued new global bifurcations that are intrinsic to the 4D system \((1)\). To identify the corresponding curves, we cataloged the “fate” of the one-dimensional unstable manifold of origin \(W^u(\mathbf{0})\) (i.e., the set of points that converge to the origin in backward time) via kneading diagrams and Lin’s method (see Figure 2) [8]. These bifurcation curves accumulate densely in a parameter region that contains the point with the known wild attractor [4]. We also analyzed the system’s attractors by computing the Lyapunov spectrum that is associated with the branch \(W^u_+(\mathbf{0})\). Doing so allowed us to identify additional regions that satisfy the required conditions, ultimately suggesting that a wild pseudohyperbolic attractor may arise in other parts of the \((\rho, \mu)\)-plane.

These results contribute to our overall understanding of the global organization of chaotic dynamics in 4D systems and may inform future studies about the mechanisms through which wild chaos emerges.

Pattern Formation Driven by Three-wave Interactions With Two Critical Wavenumbers

Laura Pinkney, graduate student, University of Leeds

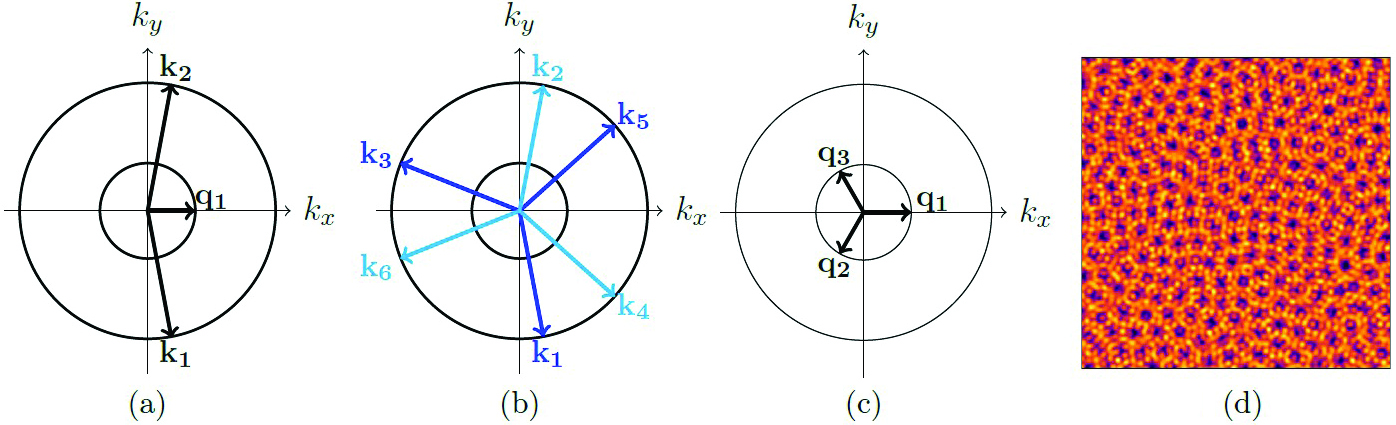
Patterns in nature arise in a variety of scenarios, such as stripes on a zebra or hexagons in a honeycomb. These examples both comprise patterns on a single length scale; stripes are composed of a single wave and hexagons arise from the interactions of three waves with the same wavenumber that are 60 degrees apart. In this simple instance of a three-wave interaction (3WI)—or resonant triad—the sum of two wavevectors equals the third. Given the existence of other pattern-forming systems with multiple length scales, we investigate problems that have two critical wavenumbers.

3WIs can explain pattern-forming behavior that is associated with the Faraday wave experiment, which periodically forces a container of fluid up and down and observes the patterns that appear on the surface. When the forcing exceeds a certain threshold, the flat state becomes unstable and yields to a variety of patterns. If the forcing contains a single frequency component, simple patterns like stripes, squares, and hexagons develop. But in the case of multiple-frequency forcing, 3WIs can arise with two critical wavenumbers and generate more complex structures such as superlattices, quasipatterns, and spatiotemporal chaos.

We consider problems with two critical wavenumbers, where resonant triads materialize between two waves of a larger wavenumber and a third wave of a smaller wavenumber (see Figure 3a). The inclusion of a second wavenumber facilitates the formation of patterns on both a rhombic and hexagonal lattice (see Figures 3b and 3c). We can represent the dynamics of these 3WIs via a set of nine complex ordinary differential equations (ODEs), with one equation for each amplitude of the wavevectors in Figure 3. This system’s generalizability means that any pattern-forming scheme that exhibits 3WIs with two wavelengths can be reduced to the same system of equations.

At DS25, I presented an analysis of a partial differential equation (PDE) that adapted the Lifshitz-Petrich equation [6] to include independent linear growth rates [9] and additional cubic nonlinearities. My collaborators and I utilized weakly nonlinear theory to reduce the PDE to the 3WI ODE system. By analyzing the stability of patterns within the ODE system, we predicted the patterns in the PDE’s solutions and used these predictions to identify regions of parameter space where we expected to find spatiotemporal chaos. We discovered significant regions of spatiotemporal chaos within our PDE, with multiple types of chaotic solutions (see Figure 3d). In the future, we hope to more deeply analyze the occurrence of different examples of chaotic dynamics.

Cellular and Parkinsonian Network Dynamics in a Conductance-based Model of the Pedunculopontine Nucleus in Rodents

Anna K. Thomas, graduate student, University of Pittsburgh

My colleagues and I develop conductance-based models of neurons in the pedunculopontine nucleus (PPN) within the brainstem to uncover the mechanisms that shape neuronal activity along motor pathways. According to recent studies, therapies that target specific deep subcortical brain areas can promote long-term motor recovery in dopamine-depleted rodents [7], but only when the PPN is intact [2]. Despite the PPN’s recognized importance, computational models of the dynamics of Parkinson’s disease rarely incorporate its contributions. Furthermore, there is no biophysically representative model of these neurons that captures the distinctive single-cell behaviors that are observed in electrophysiology experiments.

We propose a model that comprises a system of ODEs that describe the time evolution of a neuron’s membrane voltage, associated ion channel variables, and intracellular calcium concentration. The neuronal model reliably encapsulates a variety of these characteristic activity patterns, including diverse post-stimulus rebound responses, gamma-band oscillations, and the saturation of firing frequency. The presence of multiple timescales within the system—specifically for dynamical variables that represent the ionic gates of the T-type calcium channels—allows for the application of geometric singular perturbation theory, which analyzes transient model activity during post-stimulus responses. To observe and model single-cell activity on longer timescales—including high-voltage oscillations that subject the cell to slowly depolarizing ramps—we employed bifurcation analysis and demonstrated the neuronal activity’s dependence on the magnitude of applied current.

Our approach offers both mathematical and biologically mechanistic explanations of the cellular processes that underly each of these activity patterns, laying the foundation for future investigations of PPN function within motor circuits that pertain to Parkinson’s disease.

Congratulations to this year’s recipients of the Red Sock Award!

References
[1] Bonatti, C., Díaz, L.J., & Viana, M. (2005). Dynamics beyond uniform hyperbolicity: A global geometric and probabilistic perspective. In Encyclopaedia of mathematical sciences (Vol. 102). New York, NY: Springer.
[2] Cundiff, M. (2024). The path of most persistence: Investigating the mechanism of long-lasting motor rescue in a dopamine depletion mouse model [Ph.D. thesis, Center for the Neural Basis of Cognition, Carnegie Mellon University]. KiltHub.
[3] Follmann, R., Jaswal, T., Jacob, G., de Oliveira, J.F., Herbert, C.B., Macau, E.E.N., & Rosa, Jr., E. (2024). Temperature effects on neuronal synchronization in seizures. Chaos, 34(8), 083141. 
[4] Gonchenko, S., Kazakov, A., & Turaev, D. (2021). Wild pseudohyperbolic attractor in a four-dimensional Lorenz system. Nonlinearity, 34(4), 2018.
[5] Lehnertz, K., Bialonski, S., Horstmann, M.-T., Krug, D., Rothkegel, A., Staniek, M., & Wagner, T. (2009). Synchronization phenomena in human epileptic brain networks. J. Neurosci. Methods, 183(1), 42-48. 
[6] Lifshitz, R., & Petrich, D.M. (1997). Theoretical model for Faraday waves with multiple-frequency forcing. Phys. Rev. Lett., 79(7), 1261-1264.
[7] Mastro, K.J., Zitelli, K.T., Willard, A.M., Leblanc, K.H., Kravitz, A.V., & Gittis, A.H. (2017). Cell-specific pallidal intervention induces long-lasting motor recovery in dopamine-depleted mice. Nat. Neurosci., 20(6), 815-823.
[8] Patiño-Echeverría, J., Krauskopf, B., & Osinga, H.M. (2025). Global bifurcation structure of a four-dimensional Lorenz-like system with a wild chaotic attractor. Preprint, University of Auckland. Retrieved from https://www.math.auckland.ac.nz/~hinke/preprints/pko_4DLorenz.html.
[9] Rucklidge, A.M., Silber, M., & Skeldon, A.C. (2012). Three-wave interactions and spatiotemporal chaos. Phys. Rev. Lett., 108(7), 074504.