Riemann Mapping by Steepest Descent

In this issue’s column we outline a quick constructive proof of the Riemann mapping theorem.

Here’s a statement of the theorem: Any simply connected open set \(D\) in the plane that is not the entire plane can be mapped conformally and one-to-one onto an open unit disk, taking any point \(p \in D\) to the disk’s center, with the derivative at \(p\) being real and positive.

Our map is produced via a physically motivated argument: We think of a heat-conducting plate \(D\), insulated everywhere except for the boundary, as shown in Figure 1.

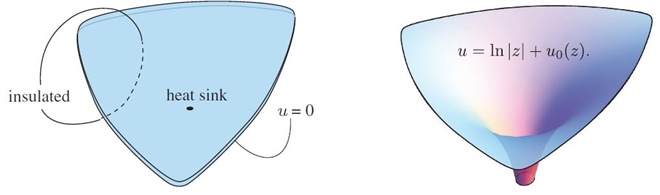
We place a heat sink at \(z = 0\), drawing \(2\pi\) calories per second, and maintain \(u = 0\) on \(\partial D\). Figure 2 shows the graph of the resulting stationary temperature distribution. Formally, we define

\[\begin{equation}\tag{1} u(z) = \mathrm{ln} | z | + u_0 (z), \end{equation}\]

where \(u_0 (z)\) is a harmonic function with boundary conditions chosen to cancel the logarithm on \(\partial D\).*

Level curves of (1) are approximately circles near \(z = 0\); more precisely, the set \(D_t = \{u \leq −t\}\) for large \(t\) is approximately a small disk \(| z |  \leq  e^{−t − {u_{0}}(0)}\) (see Figure 2).

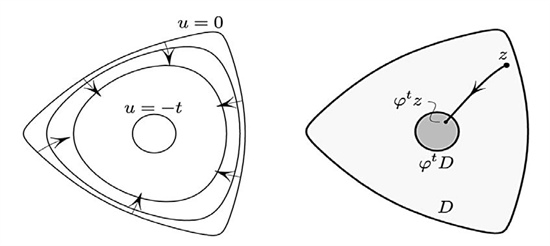
Remarkably, the flow \(\varphi^t\) of the modified gradient field

\[\begin{equation}\tag{2}\dot{z} = - \frac{1}{{|\nabla u|}^2} \nabla u\end{equation}\]

shrinks \(D\) into \(D_t\) and does so conformally—i.e., \(\varphi^t\) is almost the desired map! Indeed, \(du/dt = −1\) along (2), and thus \(\varphi^t D = D_t\) . And because the right-hand side of (2) is analytic,^† \(\varphi^t\) is conformal. By dilating \(D_t\) we obtain the desired map \(f\) in the limit:

\[\begin{equation}\tag{3} f(z) = \lim_{t \rightarrow \infty} e^t \phi^t z. \end{equation}\] 

The missing details of the proof, which are routine, can be found in [1].

*Here we use the existence of solutions of the Dirichlet problem, which limits some generality on \(D\). Details can be found in F. John, Partial Differential Equations, 4th ed., Springer, New York, 1991.

^†Since it can be written as \(1\sqrt{\nabla u} = 1/(u_x – iu_y)\), where \(U = u_x\) and \(V = −u_y\) satisfy the Cauchy–Riemann equations because \(u\) is harmonic.

Acknowledgments: The work from which these columns are drawn is funded by NSF grant DMS-1412542.

References

[1] M. Levi, Riemann mapping by steepest descent, Amer. Math. Monthly, 114:3 (2007), 246-251.