Right Results via Wrong Arguments and Wrong Results via Right Arguments

In his very entertaining book [1], V. Arnold discusses the adiabatic invariance of the pendulum — a classical problem that Einstein addressed when quantum mechanics was being born. Einstein was motivated by the desire to explain the constancy of Planck’s constant. Why does the energy-to-frequency ratio of photons remain unchanged, despite the buffeting of the emitting atom by surrounding fields? How does the atom “remember” this ratio? 

In a (probably tentative) attempt at an explanation, Einstein pointed out a classical analog of this “memory” in the simple pendulum. He showed that the energy-to-frequency \((E/ \omega)\) ratio for a linearized pendulum remains nearly unchanged if the string’s length is slowly changed by a finite amount (e.g., by half).¹ The physical quantity \(E/ \omega\) has a geometrical meaning: it is the area inside the closed orbit in the phase plane when the pendulum’s length is fixed. Such near-constant quantities are called adiabatic invariants.

In his book, Arnold deals with the linearized pendulum (see Figure 1), whose angle \(\theta\) he models by the standard textbook equation

\[\ddot \theta + \lambda \theta = 0,\tag1\]

where \(\lambda =g/\ell\) and \(\ell\) is the length of the string. If \(\ell\)—and hence \(\lambda\)—changes adiabatically (i.e., slowly), the area enclosed by the trajectory in the phase plane \((\theta, \dot \theta)\) with a frozen \(\lambda\) is an adiabatic invariant. For example, if \(\ell\) changes with small speed \(\varepsilon\) over a long time \(1/ \varepsilon\), then the area changes by the small amount \(O(\varepsilon)\) over the course of this time. The area thus changes little even if \(\ell\) changes appreciably, say by half.

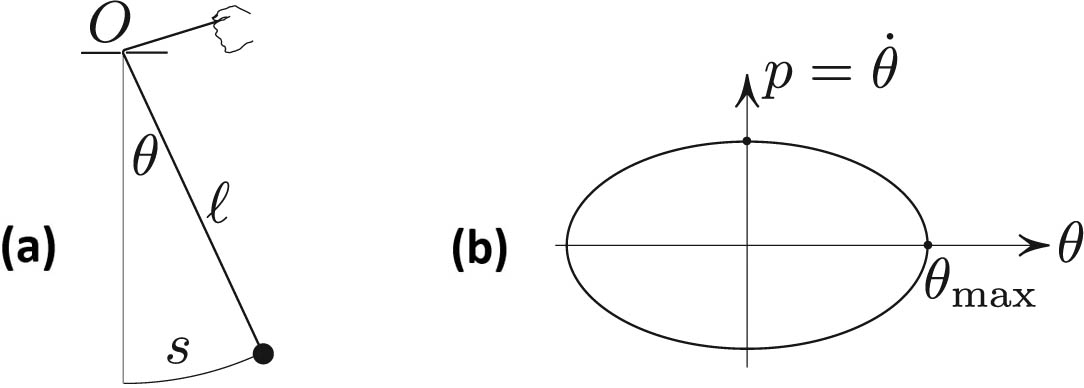
To see what this near-constancy says about the amplitude of oscillations, we observe that the trajectory in the phase plane of \((1)\) when \(\ell\) is frozen is an ellipse:

\[\theta = \theta_{\rm max}\sin \omega t, \; \; \; \; p= \dot \theta = \theta_{\rm max} \omega \cos \omega t, \]

where \(\omega = \sqrt{g/\ell}\). The area of this ellipse is \(\pi \theta_{\rm max} ^2 \omega = \pi \sqrt{g} (\theta_{\rm max}\ell ^{-1/4})^2\), so that

\[\frac{\theta_{\rm max}}{ \ell ^{1/4}}\approx {\rm const.}\tag2\]

is an adiabatic invariant. According to \((2)\), slowly shortening \(\ell\) decreases the amplitude \(\theta_{\textrm{max}}\). But this answer is wrong — the opposite happens in reality (as I show later). Arnold escaped the wrong conclusion \((2)\) by making an error in another place: he took \(\lambda = \ell/g\) instead of the correct \(\lambda = g/\ell\). This incorrect choice yielded

\[\ell ^{1/4} \theta_{\max}\tag3\]

instead of \((2)\) as an adiabatic invariant. Despite being the product of an error, \((3)\) correctly predicts that shortening \(\ell\) increases \(\theta_{\max}\). How can the right solution give the wrong answer and the wrong solution give the seemingly right answer?²

Actually, \((3)\)—although more plausible physically than \((2)\)—is still incorrect. What is going on? The resolution of this mess is that the fundamental premise—i.e., the familiar equation \((1)\)—is an incorrect model of a pendulum with variable length.

Fixing Equation \((1)\)

The standard textbook derivation of \((1)\) does not work if \(\ell\) varies; instead, we apply the rotational version of Newton’s second law to the pendulum’s bob — the point where the entire mass is concentrated:

\[\frac{d}{dt} ({\textrm{angular momentum}})={\textrm{torque}}.\tag4\]

Here, the angular momentum and torque are relative to the fixed pivot \(O\). Deciphering the quantities in \((4)\) yields the ordinary differential equation for \(\theta\): 

\[\frac{d}{dt} (\ell ^2 \dot \theta ) = - g \ell \theta\tag5\]

(after cancelling the mass and replacing \(\sin \theta\) with \(\theta\) on the right). This equation coincides with \((1)\) for \(\ell = {\rm const.}\), but not otherwise. What is the correct adiabatic invariant? We write \((5)\) as a Hamiltonian system and express the area bounded by a trajectory for frozen \(\ell\). To that end, we introduce the momentum \(p= \ell ^2 \dot \theta\) (angular, in fact) and rewrite \((5)\) as a system:

\[\dot \theta = \ell ^{-2} p, \; \; \; \; \dot p = - g\ell \theta.\]

For frozen \(\ell\), trajectories are ellipses with semiaxes \(\theta_{\max}\) and \(p_{\max} = \ell ^2 \theta_{\max} \omega\), where \(\omega\) is as before. The area of such an ellipse is

\[\pi \ell ^2 \theta^2_{\max } \omega = {\rm const.}\cdot (\ell^{3/4} \theta_{\max} ) ^2\]

using \(\omega=\sqrt{g/\ell}\), so that

\[\ell^{3/4} \theta_{\max}\approx {\rm const.}\tag6\]

is an adiabatic invariant. This is a correction of \((3)\)—which is still off by a factor of \(\sqrt{\ell}\) despite being an improvement over \((2)\)—and confirms that shortening \(\ell\) increases \(\theta_{\max}\). 

A Physical Plausibility Argument

How can we see without calculation that shortening \(\ell\) increases \(\theta_{\max}\)? As we shorten \(\ell\) by pulling in the string, we do work against the string’s tension. Averaged over one swing, this tension is a little bit more than the weight due to the centrifugal effect. So we do extra work in addition to raising the bob. This extra goes towards increasing the pendulum’s “internal” energy, i.e., the kinetic energy (K.E.) at the lowest point in the swing. And so K.E. increases as we shorten \(\ell\). But a shorter \(\ell\) and greater K.E. imply greater angular amplitude.

I must confess that when I reviewed Arnold’s book [2], I missed the fundamental error: the inapplicability of \((1)\). I only realized that something was wrong when a reader noticed that \(\ell /g\) should be \(g/\ell\), thus changing Arnold’s plausible conclusion \((3)\) to the implausible \((2)\).

A Wrong Solution with the Right Answer

Here is another twist to the story. Instead of \(\theta\), we could use the arc length \(s= \ell \theta\) that—for the pendulum of fixed length—satisfies

\[\ddot s + \lambda s = 0, \; \; \; \; \lambda = \frac{g}{\ell}.\tag7\]

This again is a wrong model of the pendulum with variable \(\ell\), just like the first equation in this article. But surprisingly, \((7)\) has the correct adiabatic invariant \((6)\) (I leave out the verification). Explaining why this wrong equation gives the correct answer is an interesting puzzle.

To sum up, the main mistake lies at the junction between math and physics. This is a bit reminiscent of electricity and plumbing, where shorts or leaks often arise at connections. To mutilate Winston Churchill’s famous phrase almost beyond recognition, rarely have so many mistakes been made in such a small problem.

¹ This “memory” is not perfect, unlike in quantum mechanics.

² In fact, a reader recently corrected Arnold’s error and came, as we just did, to the conclusion \((2)\) that—despite the correct argument—is wrong. My attempts to resolve this paradox prompted this article.

References

[1] Arnold, V.I. (2014). Mathematical understanding of nature: Essays on amazing physical phenomena and their understanding by mathematicians. Providence, RI: American Mathematical Society.
[2] Levi, M. (2020). Book review: Mathematical understanding of nature: Essays on physical phenomena and their understanding by mathematicians by V.I. Arnold, translated by Alexei Sossinsky and Olga Sipacheva. Mathemat. Intelligen., 42(1), 84-86.