Rough Volatility in Financial Mathematics

The following is a brief description from one of the editors of Rough Volatility, which was published by SIAM in 2023. The book—the first to offer a comprehensive investigation of the subject—seeks to advance reader understanding of rough volatility models by exploring their motivation and introducing a toolbox for computation and practical implementation. It is meant for researchers and graduate students in quantitative finance, quantitative analysts, and finance professionals.

More than a decade has passed since the publication of the first two working papers on rough volatility. While researchers had previously hypothesized that fractional volatility models might account for the observed power law behavior of implied volatility smiles, these models initially lacked econometric validation. Moreover, their non-Markovian nature raised serious concerns about computational tractability. 

The two aforementioned foundational papers directly addressed these challenges and now comprise the first two chapters of Rough Volatility, edited by Christian Bayer, Peter Friz, Masaaki Fukasawa, Jim Gatheral, Antoine Jacquier, and Mathieu Rosenbaum. The remaining eight chapters trace the field’s rapid development, providing an in-depth view of the sustained research activity that has transformed rough volatility into a robust and versatile modeling paradigm.

Overview and Contents

Chapter 1, titled “Volatility is Rough,” presents the empirical case for rough volatility, noting that log volatility behaves like a fractional Brownian motion with a Hurst parameter \(H\) that is significantly less than \(\tfrac{1}{2}\). The text introduces the rough fractional stochastic volatility (RFSV) model (under the physical measure \(\mathbb{P}\)) as a parsimonious framework that matches observed autocorrelation structures and scaling laws.

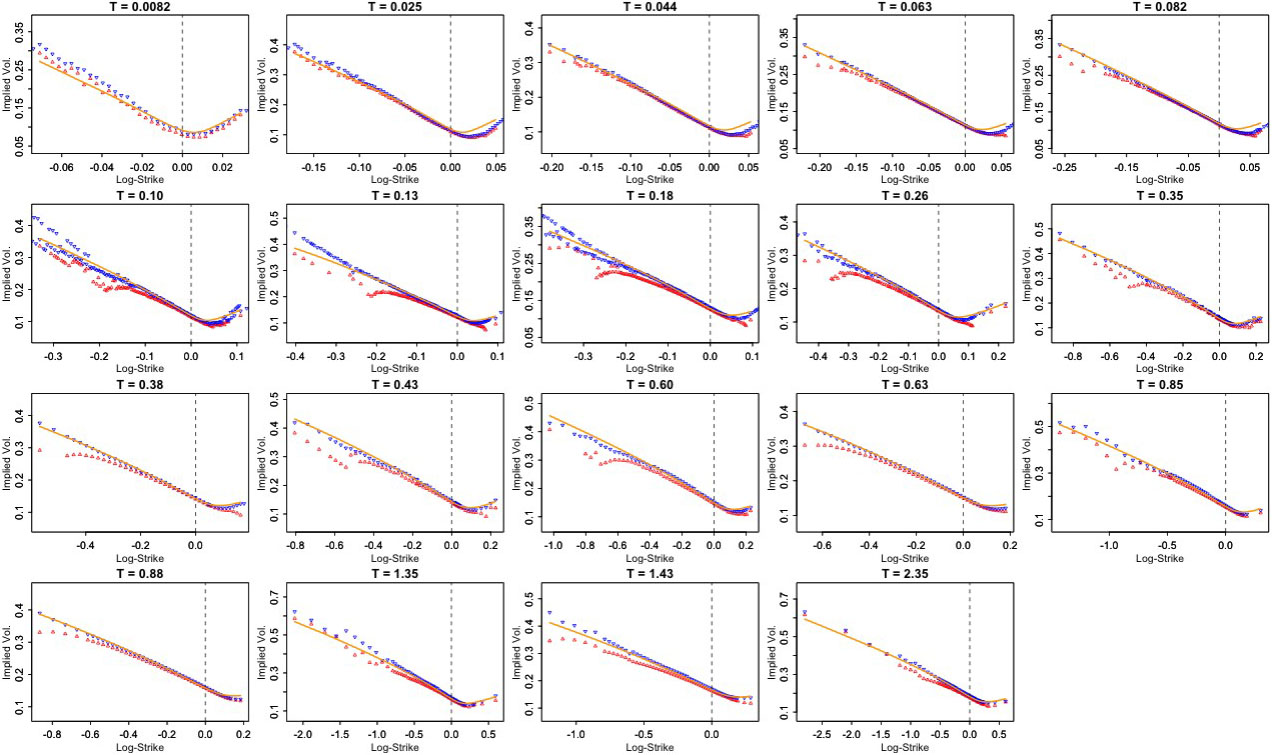
Chapter 2, “Pricing Under Rough Volatility,” constructs a dynamical pricing model called the rough Bergomi model from the RFSV model by changing measure from \(\mathbb{P}\) to the pricing measure \(\mathbb{Q}\). Notably, the history of the Brownian motion that drives the volatility process can be inferred from the forward variance curve — an object that we can extract from option prices. The highly parsimonious rough Bergomi model generates SPX smiles that closely align with observed data (see Figure 1).

Chapter 3—a reprint of the 2020 paper “No-arbitrage Implies Power-law Market Impact and Rough Volatility”—builds an economic argument for rough volatility in the framework of Hawkes processes given some basic assumptions, including absence of arbitrage, linearity of permanent impact, and the existence of market impact with a transient component.

Chapter 4 explores the rough Heston model: a natural fractional extension of the classical Heston model. The rough model preserves the classic model’s analytical tractability with a characteristic function that can be expressed in terms of the solution of a fractional version of the classical Riccati ordinary differential equation (ODE). As with the rough Bergomi model, the rough Heston model generates highly realistic smiles. Chapter 4 also touches briefly on the quadratic rough Heston model, which—though less tractable than its non-quadric counterpart—can jointly fit SPX and VIX smiles.

The rough Heston model is a member of the much larger class of rough affine models that are discussed in chapter 5. The characteristic function of such models has a representation in terms of the solution of a Riccati-Volterra equation, a natural generalization of the classical Riccati ODE. Chapter 6 then addresses hedging under rough volatility, illustrating through a simple example the improved hedging performance of strategies based on rough models.

The hybrid simulation scheme is key to the practical implementation of rough volatility models. Chapter 7, a reprint of the 2017 article “Hybrid Scheme for Brownian Semistationary Processes,” presents this scheme in detail, applying it to a generalized version of the rough Bergomi model; extended versions can be used to simulate many other rough volatility models.

Chapter 8 explores asymptotic expansions for implied volatility under rough models in various regimes. This chapter is invaluable to researchers, as it pulls together various asymptotic results from the vast rough volatility literature with consistent notation.

Chapters 9 and 10 offer a flavor of the types of mathematical development that have been inspired by rough volatility. Chapter 9, “The Forest Expansion of Forward Variance Models,” introduces the forest expansion: a combinatorial representation of characteristic functions for forward variance models as infinite sums over binary trees. Because rough volatility models are non-Markovian, the traditional tools of stochastic analysis do not apply. Subsequently, chapter 10—based on the 2020 article “Regularity Structure for Rough Volatility”—develops a strong approximation theory for rough volatility that is motivated by the work of Martin Hairer, which earned him the Fields Medal in 2014.

Intended Audience

Rough Volatility is a comprehensive reference on a growing discipline that lies at the intersection of stochastic analysis, financial modeling, and numerical computation. It is an ideal resource for graduate students, researchers, and practitioners with an interest in volatility modeling and market microstructure. While the field of rough volatility continues to evolve, this book provides a solid foundation and will remain a key reference point amidst future developments. The inclusion of empirical studies, calibration results, and numerical methods ensures its enduring relevance in both theory and practice.

Finally, the cover design by Colombian artist Oscar Murillo (winner of the 2019 Turner Prize) adds a touch of visual sophistication, making the volume equally at home on a coffee table or a bookshelf, and a perfect gift.

Enjoy this passage? Visit the SIAM Bookstore to learn more about Rough Volatility and browse other SIAM titles. And be sure to stop by the SIAM books booth at the upcoming 2025 SIAM Conference on Financial Mathematics and Engineering—which will take place from July 15-18 in Miami, Fl.—for the opportunity to purchase Rough Volatility and other texts at special conference prices.