Sea Ice Variability: Everything, Everywhere, All at Once

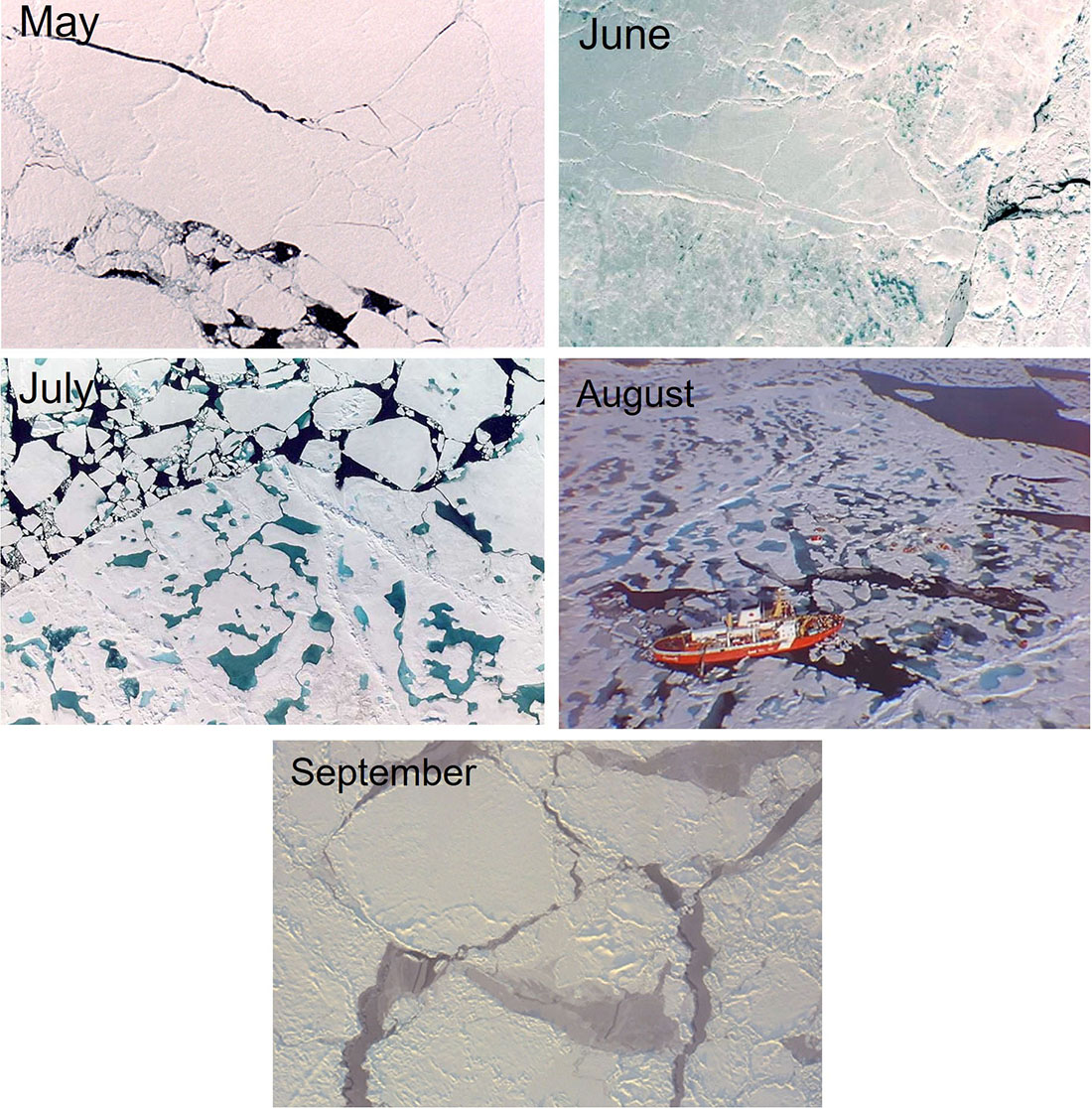
The physical properties of sea ice are highly variable in every way. There is spatial variability. Horizontally, the ice varies in thickness, snow depth, and surface characteristics; vertically, differences in ice temperature, brine volume, air volume, and crystal structure are likewise present. There is also temporal variability, as sea ice follows a seasonal cycle in which the highly reflective snow-covered ice of springtime evolves into a complex mosaic of bare ice, melt ponds, and open ocean during summer melt (see Figure 1). Several factors influence the annual ice evolution, including variations in the timing of summer melt and fall freeze-up as well as ephemeral weather events, such as winter rain-on-snow and summer snowfalls. This variability impacts all aspects of sea ice, complicating our efforts to understand and model sea ice behavior, its critical role in global climate change, and the consequences of ice-albedo feedback. 

To better comprehend ice-albedo feedback, let’s start with a simple question: Where does all the sunshine go? Or, a bit more rigorously: How is incident solar radiation partitioned between reflection to the atmosphere (albedo), absorption in the ice (absorptance), and transmission to the ocean (transmittance)? The question is simple to ask but—due to ice variability—difficult to answer.

Albedo has long been part of sea ice research. Scientists have recorded numerous albedo observations, ranging in spatial scale from in situ to aircraft to satellite. These studies have revealed a strong multiphase seasonal cycle of decreasing albedo from spring to summer—as the highly reflective, cold, snow-covered ice of springtime becomes a mixture of bare sea ice, surface ponds of meltwater, and open ocean—followed by an increase in albedo during the fall freeze-up [3, 6]. Observations of this seasonal evolution have spanned multiple locations, various time periods, and different ice types and surface conditions. Overall, we find that as ice melts, the average albedo decreases from about 0.85 in spring to 0.40 towards the end of summer melt. 

While albedo is the most important element of solar partitioning, transmittance is also significant. Transmitted light heats the upper ocean and can contribute to melting on the underside of the ice; it thus plays a central role in primary productivity for both the ice and ocean. However, transmittance is more difficult to gauge than albedo (aircraft and satellites cannot measure it), and observations are limited in space and time. In situ transmittance observations are confined to point measurements at specific locations and short under-ice surveys by underwater vehicles [4].

Radiative transfer modeling can augment these limited transmittance observations. Radiative transfer in sea ice is governed by absorption and scattering, where transmitted light decays roughly exponentially with depth. The equation of radiative transfer for a plane parallel medium is

\[-\mu\frac{dI(\tau,\mu,\phi, \lambda)}{d\tau}=I(\tau,\mu,\phi,\lambda)-S(\tau,\mu,\phi,\lambda),\]

where \(I(\tau,\mu,\phi,\lambda)\) is the spectral radiant flux per solid angle per nanometer, \(S(\tau,\mu,\phi,\lambda)\) is the scattering function, \(\tau\) is optical depth, \(\lambda\) is wavelength, \(\mu\) is the cosine of the zenith angle \((\theta)\), and \(\phi\) is the azimuth angle [1]. 

Several approaches of varying complexity can effectively model radiative transfer in sea ice. All these techniques share two basic requirements: inherent optical properties and physical properties. The inherent optical properties are the absorption coefficient (amount of absorbed light per unit distance), scattering coefficient (amount of scattered light per unit distance), and phase function (angular distribution of scattered light). Absorption coefficients for ice are well established and show a strong spectral dependence, with small values at blue wavelengths and larger values at longer wavelengths [7]. Scattering coefficients cannot be measured directly and are instead inferred from measurements of albedo and transmittance. Snow and sea ice have high levels of scatter, with coefficients that range from 800 m^-1 for dry snow to 120 m^-1 for a surface layer of loose ice grains and 1.2 m^-1 for melting ice. These coefficients do not depend on wavelength.

At a minimum, the description of physical properties must include ice thickness and the thickness of any surface layer, such as snow, loose granular ice, or ponds. We can also use physical properties of the ice interior to assign scattering coefficients for different layers. In a qualitative sense, we may say that the ice is bubbly or clear, frozen or melting; one advantage of this approach is that we can obtain a large database of scattering coefficients based on field observations. Although it is also possible to assign scattering coefficients in a quantitative way by determining the number and size distribution of the air and brine inclusion, doing so is more difficult.

Detailed treatments of radiative transfer in sea ice calculate the angular distribution of the light field that is reflected above and within the ice and transmitted through the ice. These treatments require detailed information about the ice’s inherent optical properties, including the angular distribution of scattered light. Simpler “two-stream” treatments ignore the angular distribution of the light field, assume isotropic scattering, use a qualitative description of the ice interior, and focus on reflected and transmitted irradiance. 

We now examine the spatial variability of light transmittance by incorporating physical ice properties in a two-stream, multilayer radiative transfer model. From October 2019 to September 2020, the MOSAiC research expedition made repeated, extensive kilometers-long transects to characterize the state of the Arctic sea ice cover [5]. As the melt phase neared its seasonal peak on July 25, 2020, one particular transect measured the ice thickness at 1,266 points, along with the thickness of the surface scattering layer for bare ice and the pond depth for ponded ice. 

We used these physical properties to construct a three-layer model with different scattering coefficients at each transect point. The top layer represents a surface scattering layer of loose ice grains, or the water in a melt pond. The second layer depicts the ice above the waterline, which typically has many air bubbles, and the third layer is the remaining melting ice. 

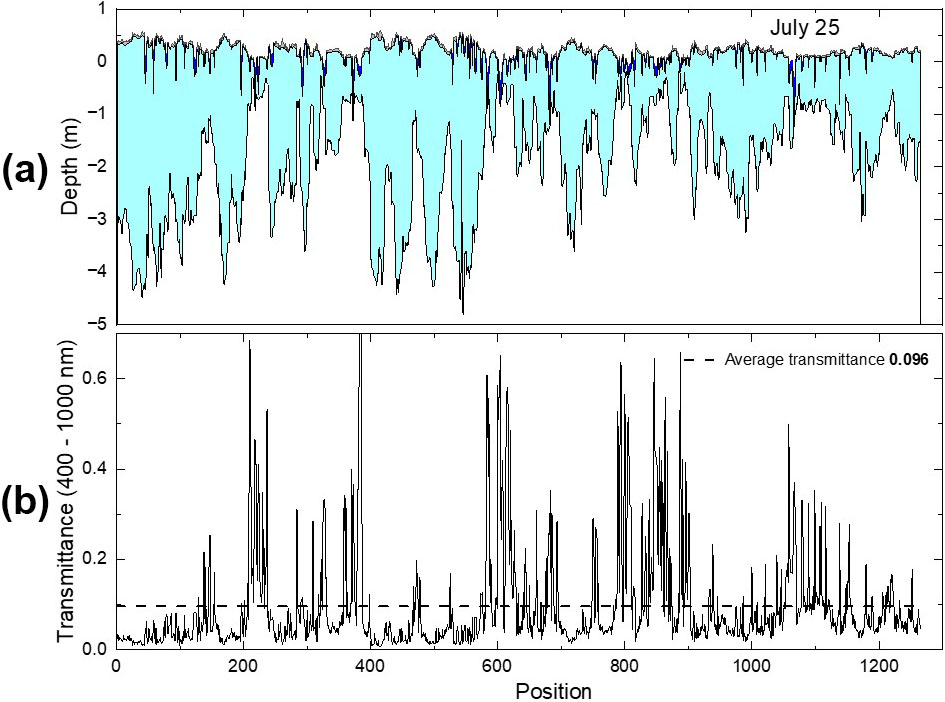
Figure 2 illustrates results from this investigation. Figure 2a shows the physical state of the ice; the gray shaded area represents the surface scattering layer and the dark blue areas are melt ponds. Large variations in ice thickness are evident, ranging from a few tenths of a meter to almost five meters. Figure 2b displays the calculated transmittance. Values span from 0.0055 to 0.76, with a mean of 0.096 and a median of 0.053. Ponds act as skylights to the ocean, and ponded ice is responsible for the largest transmittances. Although ponds only cover 18 percent of the ice surface, ponded ice contributes half of the light transmittance to the ocean.

Such extensive in situ observations of ice, snow, and pond properties as from MOSAiC are otherwise hard to come by, and this dataset can also help us evaluate other, more constrained methods of transmittance estimation. We utilized our results to compare the average transmittance—determined with the full suite of physical properties—to the five-category ice thickness distribution in the Community Earth System Model 2 (CESM2) [2]. In CESM2, each category may include a mix of bare ice and ponded ice with appropriate areal fractions. Based on the observations, we calculated the average pond fraction as well as ponded and bare ice thicknesses for each category, producing a total of 10 components for CESM2: five for bare ice and five for ponds.

The overall transmittance is 0.092 with all observations and 0.084 with the CESM2 five-category approximation. Combining these findings with the incident shortwave irradiance yields a difference in heat flux of only 1.2 W·m^-2, thus indicating that these five categories reasonably represent light transmission. CESM2 transmittances are always smaller than those that use every observation, as we rely on a linear process to determine average values for the physical properties and apply those values in an exponential function to find transmittance.

Observational and modeling research continues to improve our understanding of solar radiation’s interaction with sea ice. Arctic sea ice cover is changing, becoming younger, thinner, and smaller with every passing year. We must understand the impact of these physical changes on the ice’s optical properties, and consequently on solar partitioning.

Don Perovich delivered a minisymposium presentation on this research at the 2024 SIAM Conference on Mathematics of Planet Earth, which took place in Portland, Ore., last June.

References
[1] Chandrasekhar, S. (1960). Radiative transfer. New York, NY: Dover Publications.
[2] Danabasoglu, G., Lamarque, J.-F., Bacmeister, J., Bailey, D.A., DuVivier, A.K., Edwards, J., … Strand, W.G. (2020). The Community Earth System Model version 2 (CESM2). J. Adv. Model. Earth Syst., 12(2), e2019MS001916
[3] Light, B., Smith, M.M., Perovich, D.K., Webster, M.A., Holland, M.M., Linhardt, F., … Bailey, D.A. (2022). Arctic sea ice albedo: Spectral composition, spatial heterogeneity, and temporal evolution observed during the MOSAiC drift. Elementa: Sci. Anthropocene, 10(1), 000103.
[4] Nicolaus, M., Hudson, S.R., Gerland, S., & Munderloh, K. (2010). A modern concept for autonomous and continuous measurements of spectral albedo and transmittance of sea ice. Cold Reg. Sci. Technol., 62(1), 14-28.
[5] Nicolaus, M., Perovich, D.K., Spreen, G., Granskog, M.A., von Albedyll, L., Angelopoulos, M., … Wendisch, M. (2022). Overview of the MOSAiC expedition: Snow and sea ice. Elementa: Sci. Anthropocene, 10(1), 000046.
[6] Perovich, D.K., Grenfell, T.C., Light, B., & Hobbs, P.V. (2002). Seasonal evolution of the albedo of multiyear Arctic sea ice. J. Geophys. Res. Oceans, 107(C10), SHE 20-1-SHE 20-13.
[7] Warren, S.G. (2019). Optical properties of ice and snow. Phil. Trans. R. Soc. A, 377(2146), 20180161.