SH Wave Dispersion in Concentric Cylinders of Reinforced and Piezo-based Materials
Self-reinforced polymer composites offer numerous advantages over other composite materials, including thermoformability, high strength and stiffness, excellent impact resistance at low density, and greater biodegradability. Nowadays, most structures generally consist of two or more constituents to provide enhanced stability and sustainability. The mechanical characteristics and performance of composite materials are quite superior to those of their individual constituents.
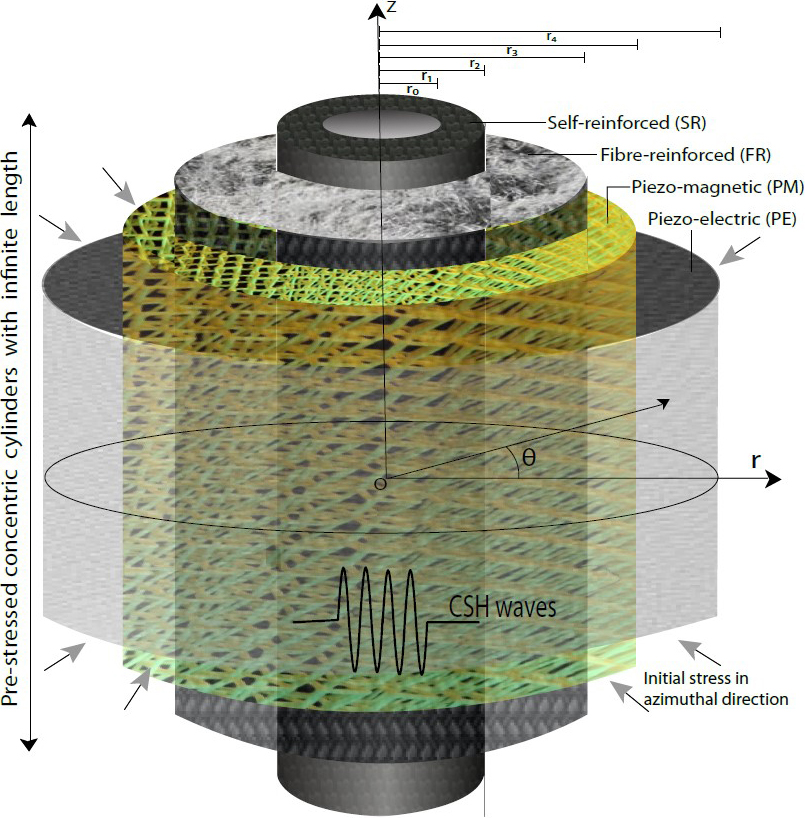
Given this information, we consider a structure that is composed of cylinders with infinite length that are circumscribed inside each other (see Figure 1). The outer part consists of piezomagnetic (PM) and piezoelectric (PE) materials, while the inner part contains self-reinforced (SR) and fiber-reinforced (FR) materials that improve stability, strength, durability, stiffness, and so forth. The reinforced materials in the inner structure allow for a better strength-to-weight ratio, and the outer cylinders overcome certain restrictions that are associated with individual PE and PM crystals such as low stiffness and brittleness. The piezo-materials help to regulate structural behavior by electrically and magnetically inducing strain fields; they also aid in electromagnetic coupling, which in turn generates the interconnected electric, magnetic, and elastic dynamic fields.
Our present work examines the detailed effects of various elastic parameters on circumferential shear horizontal (CSH) waves by means of two successive modes [1]. We find the displacements for all four materials—PM, PE, SR, and FR—in terms of Bessel’s function of the first and second kind. Additionally, the admissible boundary conditions allow us to obtain a closed-form dispersion relation for the model. We also create different graphs to analyze the effects of various essential parameters.
We specifically deduce the closed-form dispersion relation for two contrasting cases: electrically open magnetically short (EOMS) circuit conditions and electrically short and magnetically open (ESMO) circuit conditions. The dispersion curves in Figure 2 illustrate the salient features of the normalized imperfect interface parameters, initial stresses, and radii of the concentric cylinders; we note the comparative effects of each of these parameters on the wave’s phase velocity and chart every graph with two successive modes for comprehensive understanding. Interested researchers could implement this theoretical study to improve the performance of surface acoustic wave (SAW) sensors and actuators that consist of PE quartz and piezo-composite concentric cylinders.
Key Takeaways
Our current investigation establishes a mathematical model of shear horizontal (SH) wave propagation in a layered cylindrical structure that comprises SR, FR, PE, and PM material with an imperfectly bonded interface. We assume that the entire structure is initially stressed and each of the interfaces is imperfect in nature. The CSH wave’s interaction with the material properties is sensitive and responsive, and the alteration in magnitude of these elastic parameters causes a change in the wave’s phase velocity. We use EOMS and ESMO circuit conditions to carefully examine certain parameters, including normalized imperfect interfaces, cylinder radii, and initial stress. After creating graphical interpretations for the first and second modes (see Figure 2), we can summarize the salient features of the present study with the following five points:
- The normalized phase velocity of the CSH wave decreases as the normalized imperfect interface parameter increases. The phase velocity in the EOMS case is equal to or greater than the phase velocity in the ESMO case.
- The various imperfect parameters have distinct effects on the velocity of the wave. The mechanical interface imperfection parameters \(L_0\), \(L_1\), and \(L_7\) produce marginal deviations (see Figures 2a and 2b), whereas the electrically and magnetically imperfect interface parameters \(L_2\) and \(L_3\) have no evident effect on the velocity. The trends are similar for the successive modes in both the EOMS and ESMO case.
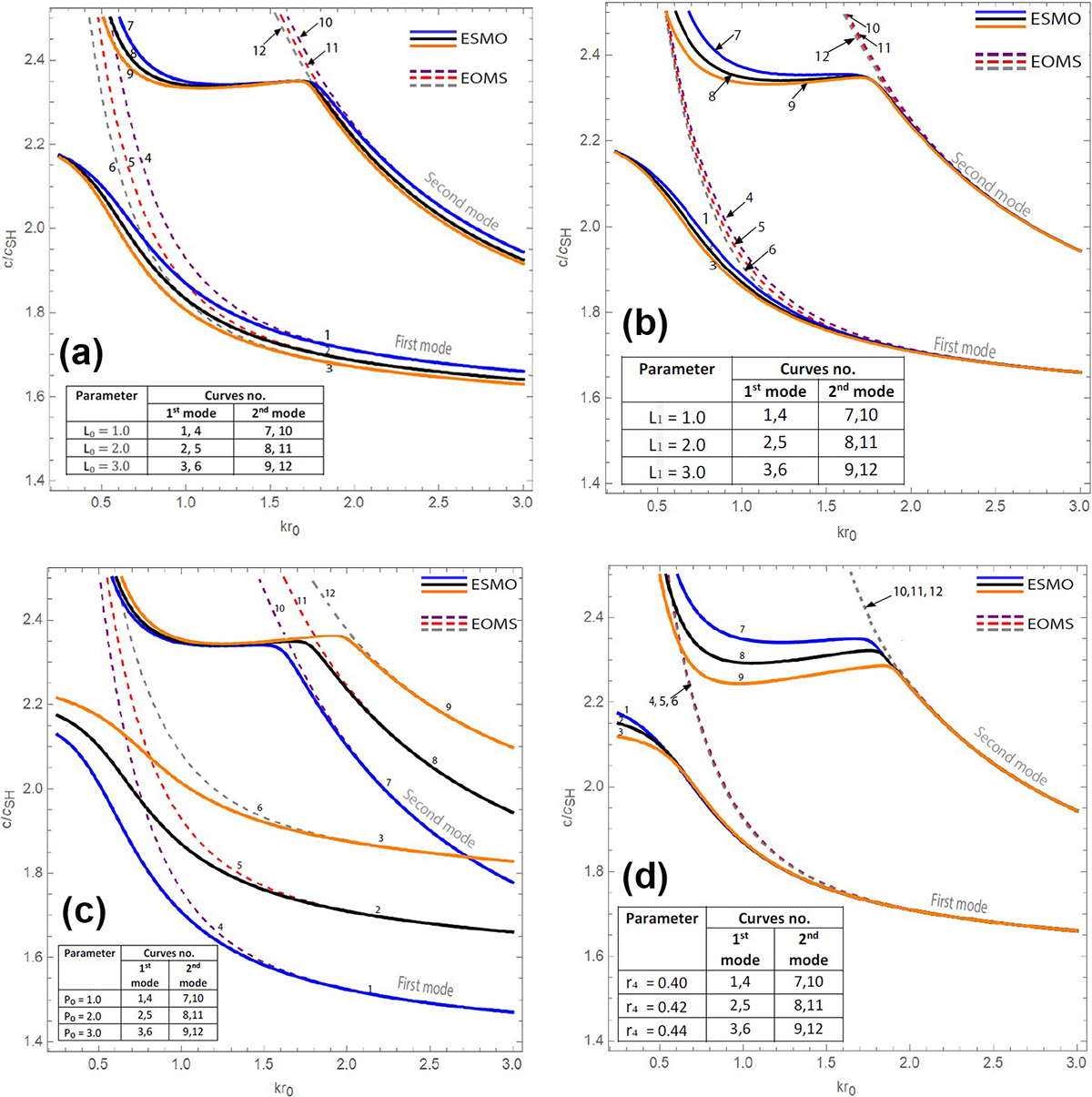
Figure 2. Phase velocity versus wavenumber for four types of variations. 2a. Phase velocity versus wavenumber for variations in \(L_0\). 2b. Phase velocity versus wavenumber for variations in \(L_1\). 2c. Phase velocity versus wavenumber for variations in \(P_0\). 2d. Phase velocity versus wavenumber for variations in \(r_4\). Figure courtesy of the authors. - The coupled imperfect interface parameter \(L_4\) yields an ambiguous result as the EOMS magnitude approaches a certain wavenumber range in the first mode of the curve. In contrast, the coupled magneto-mechanical and magneto-electrical parameters \(L_5\) and \(L_6\) have no effect on the phase velocity, even when we change their numerical values. However, a slight but notable variation may exist in EOMS (first mode) and ESMO (second mode) cases with \(L_4\) variation.
- The initial stress parameter \(P_0\) that is associated with the FR cylinder delineates a smooth diversion of phase velocity in both the EOMS and ESMO case (see Figure 2c). Magnetic and electric permeability carry the same magnitude of the velocity until \(kr_0=1.5\) and \(kr_0=2.2\) for the first and second modes, respectively. Conversely, the initial stress parameter \(P_1\) triggers a slight variation in phase velocity when it changes from \(P_1=1.0\) to \(P_1=3.0.\) The initial stress parameter \(P_2\) in the PE cylinder produces a sudden change in the ESMO case but does not affect the EOMS case for both successive modes. As the interface becomes magnetically and electrically permeable, the influence of initial stress diminishes and its effect on the velocity is less regular.
- A consistent growth in the radius of the hollow cylinder results in a significant hike in the phase velocity (see Figure 2d). As the radius \(r_0\) increases, the thickness of the SR cylinder decreases. This condition greatly impacts the velocity of the wave in the first and second modes. The velocity decreases as the hollowness of the SR material increases, but the nature of the curve is reversed in the first mode as soon as the wavenumber decreases. Additionally, changing the thicknesses of the SR and FR cylinders reversely affect the phase velocities. However, the descending thickness of PM and PE cylinders consistently alters the velocity in the first mode without really impacting the second mode. It is important to note that as soon as the PE cylinder becomes thicker than the PM cylinder, the velocity becomes extensively sensitive — thereby making it a perfect structure for sensing purposes in SAW devices.
Conclusions
The working phenomena of acoustic wave devices depend heavily upon the limitations of the wave’s transference, and the multilayered structure of these devices significantly contributes to their keen sensing abilities. Based on our present study, scientists could utilize a PE cylinder to analyze the impacting wave on a pressurized thin aluminum plate that is covered with a composite material; one could also form a PE transducer system to monitor corrosion-like defects in large-diameter pipes. Because PE and PM materials are useful in engineering contexts, the present investigation may find applications in aerospace engineering, the automotive industry, and mechanical metallurgy. In fact, many SAW devices employ PE and PM cylindrical layered structures to achieve high performance. Ultimately, we hope that our work will help to optimize the performance of acoustic wave devices, transducers, sensors, and experimental setups that identify imperfections.
Sunita Kumawat delivered a minisymposium presentation on this research at the 2023 SIAM Conference on Computational Science and Engineering (CSE23), which took place in Amsterdam, the Netherlands. She received funding to attend CSE23 through a SIAM Student Travel Award. To learn more about Student Travel Awards and submit an application, visit the online page.
SIAM Student Travel Awards are made possible in part by the generous support of our community. To make a gift to the Student Travel Fund, visit the SIAM website.
References
[1] Kumawat, S., & Vishwakarma, S.K. (2023). Circumferential SH wave in piezo-reinforced composite structure with imperfect interface bonding. Appl. Math. Model., 123, 311-331.
About the Authors
Sunita Kumawat
Assistant professor, SR University
Sunita Kumawat is an assistant professor of mathematics in the Department of Computer Science and Artificial Intelligence at SR University in Warangal, India. She completed a Ph.D. in the Department of Mathematics at BITS Pilani, Hyderabad Campus. Kumawat qualified for the CSIR-UGC NET, a key criterion for lectureship in India. Her areas of expertise include elastic wave dispersion, numerical modeling, wave scattering, and machine learning applications.
Sumit Kumar Vishwakarma
Associate professor, Birla Institute of Technology and Science Pilani, Hyderabad Campus
Sumit Kumar Vishwakarma is an associate professor in the Department of Mathematics at the Birla Institute of Technology and Science Pilani, Hyderabad Campus in India. He earned a Ph.D. from the Indian Institute of Technology, Dhanbad, and completed postdoctoral research at Harbin Engineering University in China. Vishwakarma has also served as a visiting professor at Tokyo University of Science and currently focuses on advancing research on the evaluation of Green's functions in scattering problems.
Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.