Simulating the Dynamics of Large Flocks of Birds

In many parts of the world, European starlings (Sturnus vulgaris) congregate in large groups called murmurations. These flocks move in rapid, seemingly spontaneous ways while maintaining strong spatial coherence (see Figure 1). Although the exact purpose and mechanism of this behavior is unknown, some have theorized that it allows the starlings to evade predatory hawks and falcons [4]. Regardless of their purpose, murmurations offer a compelling mystery for scientists and casual observers alike.

We aim to investigate the behavior of very large flocks of birds, with populations on the order of 10,000 individuals. To do so, we employ an agent-based simulation that computes the behavior of each individual bird in the flock based on a specific set of interaction rules with nearby birds. We thus hope to find the individual behaviors that lead to dramatic collective motions like murmurations in large groups. Since such a simulation’s computational complexity grows quadratically with flock size [6], researchers have typically limited agent-based flocking simulations to a small number of birds in order to maintain a reasonable simulation time.

Fortunately, agent-based models can effectively utilize the parallel computational infrastructure of modern computer hardware. Because each bird makes an independent decision at every time step in the simulation, we can parallelize most of the computation with very little overhead. Nearly all modern computers have some form of graphics processing hardware, which provides a substantial speedup in the solution of general problems that can be further enhanced with a massively parallel approach [3]. To take advantage of such hardware, we implement our flocking simulation via the WebGL (Web Graphics Library) application programming interface for JavaScript; WebGL also allows the simulation to run in any modern web browser on hardware ranging from a laptop to a cell phone.

Flocking models typically encode three primary goals for every bird in a flock [6]:

1. Cohesion: stay near other birds in the flock
2. Separation: avoid collisions with other birds 
3. Alignment: fly in the same direction as nearby birds.

Each bird only reacts to other birds within a limited range. One can design and implement models that obey these rules in numerous ways, including by setting explicit rules that update acceleration to meet the objectives or treating each bird as a point mass that interacts through a potential function. In our case, we encode the rules as a cost function for each bird and use model predictive control (MPC) to allow the birds to predict their optimal course by minimizing the cost function [5]. The cost function for an individual bird \(i\) with the set of neighbors \(N(i)\) is given by

\[J_i(x_i, v_i) = \frac{\chi}{|N(i)|} \sum_{j\in N(i)} \|x_i - x_j\|^2 + \omega \sum_{j\in N(i)} \frac{1}{\|x_i - x_j\|^2} + \frac{\alpha}{|N(i)|} \sum_{j \in N(i)} \|v_i - v_j\|^2.\]

Here, \(x\) and \(v\) are the estimated acceleration and velocity of each bird given a specific acceleration to be taken by bird \(i\), and \(\chi\), \(\omega\), and \(\alpha\) are weighting parameters. The first term of the cost function corresponds to the cohesion goal, the second term corresponds to the separation goal, and the third term encodes the alignment goal. A benefit of the MPC approach is that we can add additional terms to this cost function that represent behaviors such as predator and obstacle avoidance or target-seeking.

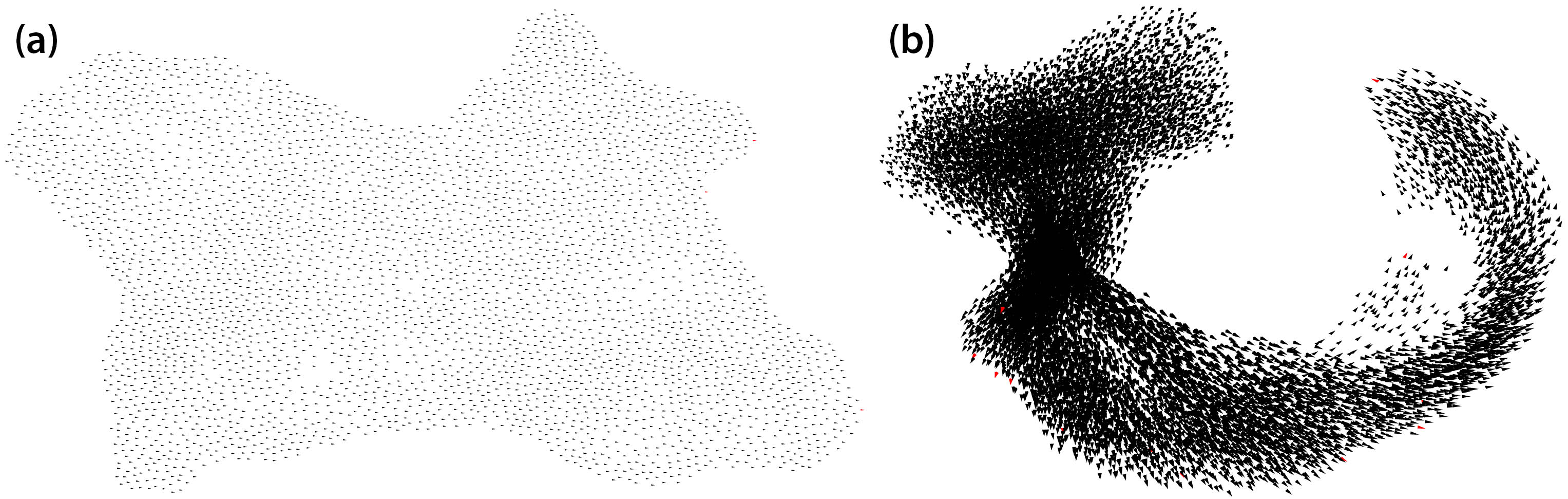
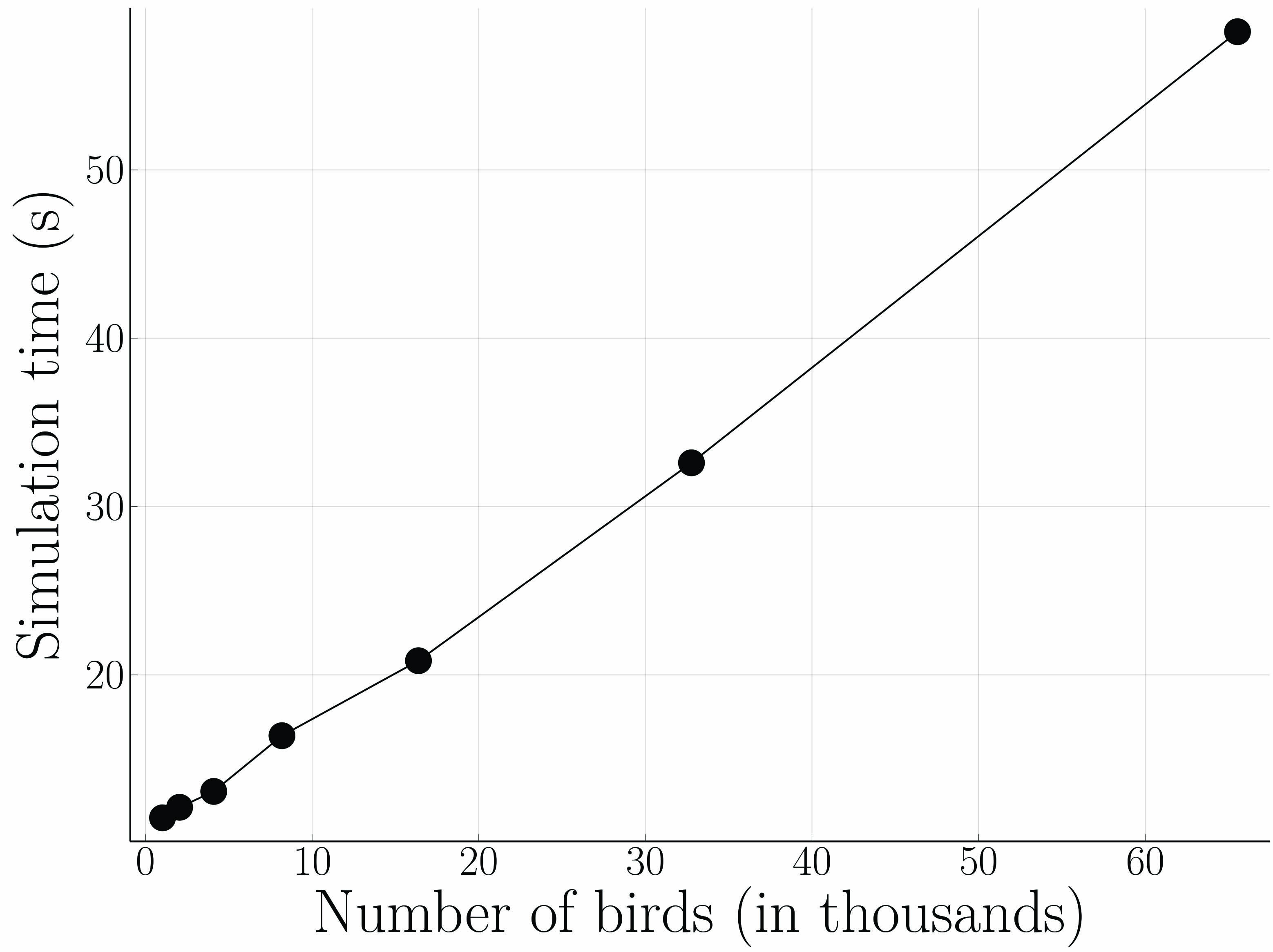
Figure 2 displays two sample screenshots from the simulation, which runs in approximately real time for up to 65,536 birds and permits interactive parameter tuning to adjust the flock’s behavior. Figure 3, which provides a plot of the required simulation time for varying flock sizes, demonstrates that the simulation’s parallel nature allows for nearly linear performance scaling with flock size in practice. Additionally, the program contains a mechanism that runs a series of simulations to test the result of changing specified parameter values. We used this method to tune hyperparameters and optimize the cost function and MPC behavior, while also informing default values for parameters like the cost function weights \(\chi\), \(\omega\), and \(\alpha\) in order to maintain a cohesive flock under various conditions. Other parameters, such as the birds’ movement capabilities, are taken from observational studies when possible [1, 2].

To quantitatively understand the effects of these parameters on the flock, we implemented several metrics in the simulation. We can record some of these metrics—such as the average distance between each bird and its neighbors—while the simulation runs, while other metrics are more computationally expensive and thus only measured upon request through the user interface. One important metric is the number of sub-flocks, which indicates whether the flock has split up or remained a cohesive group. These metrics have already proven useful for tuning and validating aspects of the model. For example, the average distance between each bird and its neighbors does not change as the number of birds increases, and flocks that begin together can remain as one group even when there is a significant amount of noise (an expression of turbulence or limitations in the birds’ ability to control their movement). On the other hand, these metrics also denote areas of improvement for the current model, as the flock tends to break up when we add predators to the simulation.

WebGL-accelerated flocking has proven useful for the creation of large-scale simulated flocks without extreme hardware requirements. Moving forward, we intend to further develop our model and simulation toward the reproduction of starling murmuration patterns.

Max Comstock delivered a contributed presentation on this research at the 2022 SIAM Conference on the Life Sciences (LS22), which took place concurrently with the 2022 SIAM Annual Meeting in Pittsburgh, Pa., last year. He received funding to attend LS22 through a SIAM Student Travel Award. To learn more about Student Travel Awards and submit an application, visit the online page. 

References

[1] Attanasi, A., Cavagna, A., Del Castello, L., Giardina, I., Grigera, T.S., Jelić, A., …Viale, M. (2014). Information transfer and behavioural inertia in starling flocks. Nat. Phys., 10(9), 691-696. 
[2] Ballerini, M., Cabibbo, N., Candelier, R., Cavagna, A., Cisbani, E., Giardina, I., & Zdravkovic, V. (2008). Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study. Proc. Nat. Acad. Sci., 105(4), 1232-1237.
[3] Kaboudian, A., Cherry, E.M., & Fenton, F.H. (2019). Real-time interactive simulations of large-scale systems on personal computers and cell phones: Toward patient-specific heart modeling and other applications. Sci. Adv., 5(3), eaav6019.
[4] King, A.J., & Sumpter, D.J. (2012). Murmurations. Curr. Biol., 22(4), R112–R114.
[5] Mehmood, U., Paoletti, N., Phan, D., Grosu, R., Lin, S., Stoller, S.D., … Smolka, S.A. (2018). Declarative vs rule-based control for flocking dynamics. In Proceedings of the 33rd annual ACM symposium on applied computing (SAC’18) (pp. 816-823). Pau, France: Association for Computing Machinery.
[6] Reynolds, C.W. (1987). Flocks, herds and schools: A distributed behavioral model. In Proceedings of the 14th annual conference on computer graphics and interactive techniques (SIGGRAPH’87) (pp. 25-34). Anaheim, CA: Association for Computing Machinery.