Simulation-based Volcanic Hazard Assessment

Large granular volcanic events—pyroclastic flows—are rare yet potentially devastating for communities situated near volcanoes. The typical process for assessing pyroclastic flow hazards for areas downstream from a volcano relies almost exclusively on expert opinion and historical record. To expect behavior we have seen previously is human nature, but it is a poor basis for hazard assessment and can seriously underestimate the hazard potential.

Over the last decade, experts have begun to supplement their understanding of volcanic hazards with realistic geophysical flow simulations. One widely used software implementation of a granular flow model, TITAN-2D, simulates course, depth, and velocity for a pyroclastic flow of specified volume and initial direction over a region whose topography is available as a digital elevation map. (You can run it yourself at www.vhub.org.)

Flow simulations are not computationally cheap, and very-large-volume events that lead to inundation in regions not previously affected are extremely rare. For these reasons, we must consider certain questions: What are the right scenarios to simulate? What are the right values of physical parameters, such as basal and internal friction, to use in flow simulations?

Ultimately, these are questions of uncertainty quantification. In the framework of quantifying uncertainties through probability distributions, we can state the questions more precisely: How can we reflect aleatoric variability (natural randomness) of physical scenarios and epistemic uncertainty (uncertainty in model characterization) of such probability distributions in the output of flow simulations? How can we use flow simulations to calculate the probability of volcanic hazards and ultimately produce a probabilistic hazard map? How can we achieve these objectives in a computationally efficient manner?

A common approach to simulation-based geophysical hazard assessment first characterizes the aleatoric variability of physical scenarios by fitting a probability distribution; from this distribution, it draws “sample” scenarios for which the geophysical simulations are run, and computes the probability of a resulting hazard. (The term “samples” is used loosely—they could be collocation points for a polynomial chaos scheme, inputs for statistical emulators, or traditional Monte Carlo samples.)

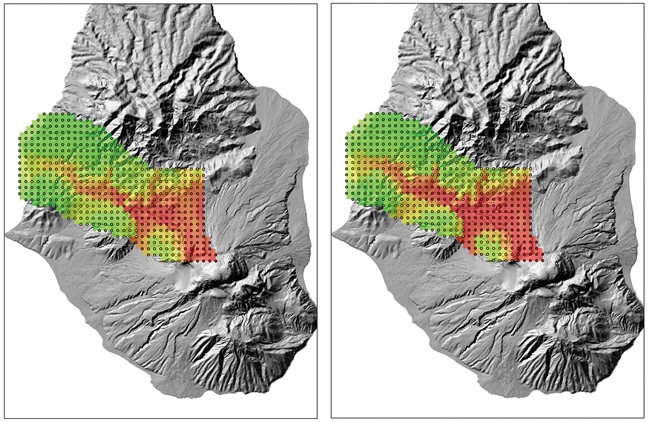
There are two significant, confounding problems with this approach. First, it results in sample scenarios and simulations that are tied to a single probability distribution. To update this distribution as new data or information comes online, or to integrate the distribution over a prior distribution of parameter values as in a Bayesian uncertainty analysis, samples from a different distribution, and hence new simulations, are required. Secondly, it is the rare tail-events from the physical scenario distribution that lead to hazards. The strategy used, therefore, must be careful to target simulations on the tail. The nature of rare events, however, dictates that there is little to no data in this region; epistemic uncertainty remains large in this region of interest, even if not over the rest of the distribution. Furthermore, as large-scale geophysical simulations are precious (in terms of man hours and computation hours), there is a natural desire to avoid “wasting” them on scenarios that seem quite unlikely.

In our minisymposium at the first SIAM uncertainty quantification conference, we proposed a rather different strategy that is computationally efficient, naturally handles rare events, and allows a flexible approach to quantifying epistemic uncertainties in geophysical hazard assessment. Our impetus for devising this approach was the realization that a TITAN-2D run for a given physical scenario and set of physical model parameters will result in flow inundation at a map point of interest (or not) regardless of how probable that scenario and parameterization are.

Our approach seeks to separate state space into regions that result in inundation at a specific map point and regions that do not. The first step in solving this inverse problem is to run TITAN-2D with inputs chosen by a space-filling design, which samples over large swaths of scenario and parameter space. We then fit a statistical emulator to these flow heights (TITAN-2D outputs). A statistical emulator can be thought of as a cheap surrogate that approximates flow height for all scenarios between those of the TITAN-2D runs; the statistical emulator simultaneously provides estimates of the error incurred by using such an approximation.

With a low, threshold height as an indication of inundation, we can invert this emulated response surface to obtain an inundation contour—which separates state space into “dangerous” and “safe” scenarios. Because the evaluation of emulators is effectively free in a computational sense, we can easily generate contours over a wide range of physical parameters. Doing so gives us samples from a probability distribution on these contours, so that this uncertainty can also be quantified and propagated. These contours then replace indicator functions in probability calculations, which means that any Monte Carlo scheme will automatically sample the important regions of state space. Moreover, for a probability calculation with a different distribution representing aleatoric variability, no new geophysical simulations are required. Such calculations can thus be done in minutes instead of hours or days. In effect, this methodology allows efficient comparisons of different models of aleatoric variability.