Single-particle Tracking and the Complexity of the Cytoskeleton
Many processes occur simultaneously within live cells, and all are important to overall cell health, behavior, and function. Scientists typically study each individual process according to its own complex dynamics. As such, mathematical models of intracellular transport tend to focus on the individual transport of organelles that are essential to a specific cellular function. Recent advances have produced models that can understand and simulate each individual intracellular process and predict future behavior, thus inspiring researchers to attempt to identify the relationships between these processes and relate them to the underlying dynamics of the cell cytoskeleton.
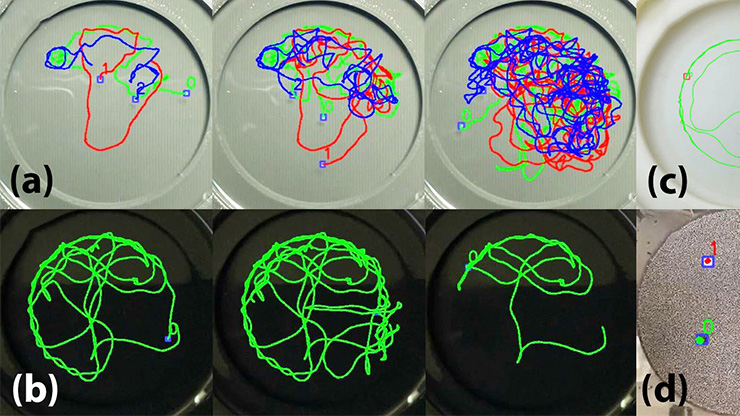
![<strong>Figure 1.</strong> Application of the changepoint analysis method to lysosomal motion. <strong>1a.</strong> The original trajectory, which was captured at a frame rate of 20 frames per second. Green marks the start of the trajectory and red marks its end. <strong>1b–1c.</strong> The \(t\)-versus-\(x\) and \(t\)-versus-\(y\) time series of the original trajectory. The dashed lines represent the changepoints and the red line indicates the result of the segmentation procedure. <strong>1d.</strong> The estimated duration, speed, and state of each segment in the trajectory. A segment is considered to be <em>motile</em> if its estimated speed is greater than 100 nanometers per second. Figure courtesy of [1].](/media/upmnlvbo/figure1.jpg)
Single-particle tracking is the study of particle motion in a medium. In our context, the cellular cytoplasm is the medium and lysosomes—membrane-bound organelles that facilitate processes like endocytosis, phagocytosis, autophagy, and degradation—are the particles. We can track the position of each fluorescently tagged lysosome as it travels across the cytoskeleton, which is a network of dynamic filaments that transports organelles within the cell and helps cells maintain their shape and internal organization. Lysosomes are transported via molecular motors and the endoplasmic reticulum (ER), the latter of which is a continuous membrane system that contains the organelles and the cytoskeleton. Cells require intracellular transport to function, and the structure of the cytoskeleton and ER play a significant role in facilitating this transport.
Our research uses stochastic processes, Bayesian inference, data-driven modeling, and statistical analysis to better understand the following topics: (i) the characterization of lysosome motion in live cells, (ii) the impact of cellular location and lysosome size on lysosome motion, (iii) the effect of ER structural changes on lysosome motion, and (iv) the connection between lysosome trajectories and the microtubule network.
Our data-driven approach seeks to fit a mathematical state-switching model to a large set of lysosome trajectories and use statistical tests and continuous-time Markov chains to determine the appropriate parameters. For each lysosome trajectory, we apply a Bayesian changepoint analysis method to the \(x\) and \(y\) coordinates over time. Doing so enables the efficient segmentation of each trajectory into two distinct states of motion: motile (when the speed is greater than or equal to 100 nanometers per second) or stationary. An orthogonal least squares regression and maximum likelihood estimation determine each segment’s speed, and a Markov chain model allows for the switch between the two states [1] (see Figure 1). Each trajectory spends an exponentially distributed amount of time in each state and has a particular probability of switching between states; we infer the rate parameters and probabilities via a Bayesian approach. Using this information, we compute the state periods, i.e., the amount of time that trajectories spend in consecutive segments of the same state over the long term. We determine these parameters for trajectories in the periphery and perinuclear regions of the cell with lysosomes of various sizes (from small to large).
![<strong>Figure 2.</strong> Decrease in vesicle motility due to disruption of the cytoskeleton, endoplasmic reticulum (ER), and ribosomes. Error bars show normalized 95 percent confidence intervals (CIs); CIs that do not overlap determine significance. Disruption of microtubules and the ER has the greatest impact on vesicle motility. Figure courtesy of [2].](/media/rfwn3x0n/figure2.jpg)
Overall, our work shows that (i) lysosome transport does indeed switch between the motile and stationary states, (ii) lysosomes in the perinuclear region spend less time in motile segments, and (iii) large lysosomes move more slowly during motile segments than small lysosomes. Intracellular location is hence an important factor in lysosome transport.
We can also use this mathematical model to identify the underlying mechanisms that affect lysosome transport via two approaches: (i) crowding the cell with ribosomes and (ii) measuring lysosome transport with respect to disruption of the ER, microtubules, and other cytoskeleton filaments [2]. Our results indicate that microtubules and the ER have the greatest impact on lysosome transport (see Figure 2).
More recently, we have begun to wonder about the optimal frame rate for capturing lysosome trajectories. Our current analysis is based on 20 hertz data, or trajectory data that is captured at 20 frames per second [1, 2]. We intend to use existing analyses and models to build simulations of lysosome trajectories at various frame rates in search of the optimal rate, as well as develop a framework that applies to any type of intracellular single-particle tracking data. Ultimately, connecting the many models of different intracellular processes will improve our understanding of the teamwork between organelles in live cells.

Keisha Cook delivered a minisymposium presentation on this research at the 2023 SIAM Conference on Applications of Dynamical Systems, which took place in Portland, Ore., in May 2023. She also delivered a minisymposium presentation on this research at the 10th International Congress on Industrial and Applied Mathematics (ICIAM 2023), which took place in Tokyo, Japan, in August 2023. Cook received funding to attend ICIAM 2023 through a SIAM Travel Award that was supported by U.S. National Science Foundation grant DMS-2233032. To learn more about SIAM Travel Awards and submit an application, visit the online page.
Acknowledgments: This work is supported by funding from the NSF-Simons Southeast Center for Mathematics and Biology (SCMB) through grants NSF-DMS1764406 and Simons Foundation-SFARI 594594.
References
[1] Rayens, N.T., Cook, K.J., McKinley, S.A., & Payne, C.K. (2022). Transport of lysosomes decreases in the perinuclear region: Insights from changepoint analysis. Biophy. J., 121(7), 1205-1218.
[2] Rayens, N.T., Cook, K.J., McKinley, S.A., & Payne, C.K. (2023). Palmitate-mediated disruption of the endoplasmic reticulum decreases intracellular vesicle motility. Biophy. J., 122(7), 1355-1363.
About the Author
Keisha Cook
Assistant professor, Clemson University
Keisha Cook is an assistant professor in the School of Mathematical and Statistical Sciences at Clemson University. She develops mathematical models of various biological, physical, and environmental processes and uses stochastic techniques and Bayesian inference methods to make predictions that lead to a better understanding of each process.

Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.