Social and Environmental Drivers of Opioid Risk: A Topological Study

The ongoing opioid crisis in the U.S. remains a complex and daunting public health challenge. Opioid use disorder is a multifaced disease that is usually associated with feelings of hopelessness and social isolation; no single factor can directly predict misuse. Because the crisis was initially driven by prescription practices, national initiatives and legislative actions have sought to reduce the number of opioid prescriptions — successfully leading to a decrease from 257.9 million in 2011 to 143.4 million in 2020 [2]. Despite these efforts, no corresponding decline in opioid-related overdose deaths has occurred. In fact, fatal opioid overdose rates have increased from 7.3 per 100,000 people in 2011 to 24.7 per 100,000 people in 2021 [4]. Our goal is to identify the social and economic factors that contribute to the opioid epidemic, then use these factors to develop predictive models that identify at-risk individuals in clinical settings.

When generating our models, we initially considered components of the Social Vulnerability Index (SVI): a composite risk measure that was developed in 2006 by the U.S. Centers for Disease Control and Prevention, Agency for Toxic Substances and Disease Registry, and Office of Environmental Health Emergency Management to quantify a community’s resilience to disaster (see Figure 1). State and local health agencies utilize SVI data to inform community-based health initiatives, as regions with a high SVI ranking may require additional aid before, during, or after a disaster takes place. We applied ideas from topological data analysis (TDA) to the SVI space in order to identify regions that are at a high risk of opioid overdoses and better understand the SVI data space in the context of downstream predictive models.

TDA is a collection of methods that employ algebraic topology to characterize the shape of a dataset. Techniques often use a sequence of simplicial complexes to approximate the shape of a dataset and study its topological invariants, which reveal the shape across multiple scales. In our setting, the standard TDA workflow cannot sufficiently quantify the SVI data space because typical methods are based on Euclidean distance. We aimed to preserve a notion of geospatial proximity in our construction and thus generated simplicial complexes based on adjacencies between census tracts and their “distances” in the SVI space. Our construction respects Tobler’s first law of geography—which states that “everything is related to everything else, but near things are more related than distant things” [5]—and retains geographical information in the topological representation.

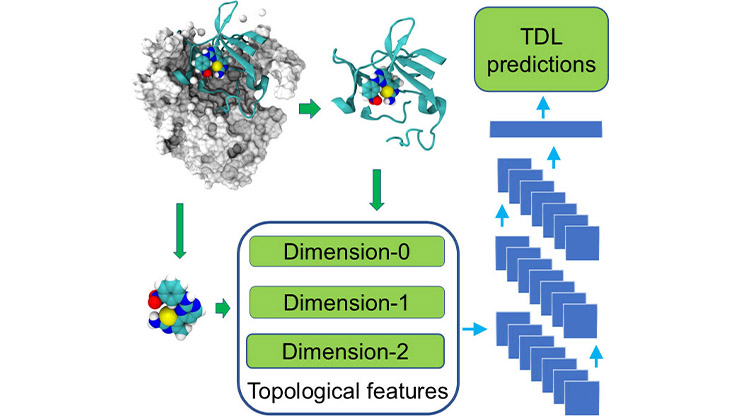
However, the ensuing topological representation is not amenable to machine learning algorithms. To prepare these multisets for our machine learning method, we used the persistence image transform and embedded the topological data in Euclidean space [1]. The resulting images are used as input to a neural network that is trained to predict whether a U.S. county is at high risk of opioid overdose events; Figure 2 illustrates our processing pipeline. We considered several different high-risk thresholds—top five, 10, or 20 percent—based on the number of overdoses within a calendar year. By studying these risk thresholds, we can better understand the components within the SVI that drive opioid overdose risk at various levels.

To further refine our study, we intend to add a temporal component that will help us examine different factors’ impacts on risk over time. We also plan to incorporate a multimodal input into our model in order to augment our topological features with numeric or text data. Ultimately, we hope to develop a predictive model for clinical use within the U.S. Department of Veterans Affairs to estimate opioid-related health outcomes based on an individual’s unique set of factors.

Adam Spannaus delivered a minisymposium presentation on this research at the 2024 SIAM Conference on Mathematics of Data Science, which took place in Atlanta, Ga., last October.

Notice: This manuscript has been authored by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the U.S. Department of Energy (DOE). The U.S. government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for U.S. government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan. 

References
[1] Adams, H., Emerson, T., Kirby, M., Neville, R., Peterson, C., Shipman, P., … Ziegelmeier, L. (2018). Persistence images: A stable vector representation of persistent homology. J. Mach. Learn. Res., 18(8), 1-35.
[2] American Medical Association. (2021). Physicians’ actions to help end the nation’s drug-related overdose and death epidemic — and what still needs to be done (2021 Overdose Epidemic Report). Chicago, IL: American Medical Association.
[3] Hu, J., Shen, L., Albanie, S., Sun, G., & Wu, E. (2017). Squeeze-and-excitation networks. Preprint, arXiv:1709.01507.
[4] State Health Access Data Assistance Center. (n.d.). The opioid epidemic in the United States. Retrieved from https://www.shadac.org/opioid-epidemic-united-states.
[5] Tobler, W.R. (1970). A computer movie simulating urban growth in the Detroit region. Econ. Geogr., 46, 234-240.