Some Light Geometry

Of the two geometrical curiosities below, the first involves zero work and the second (almost) zero words.

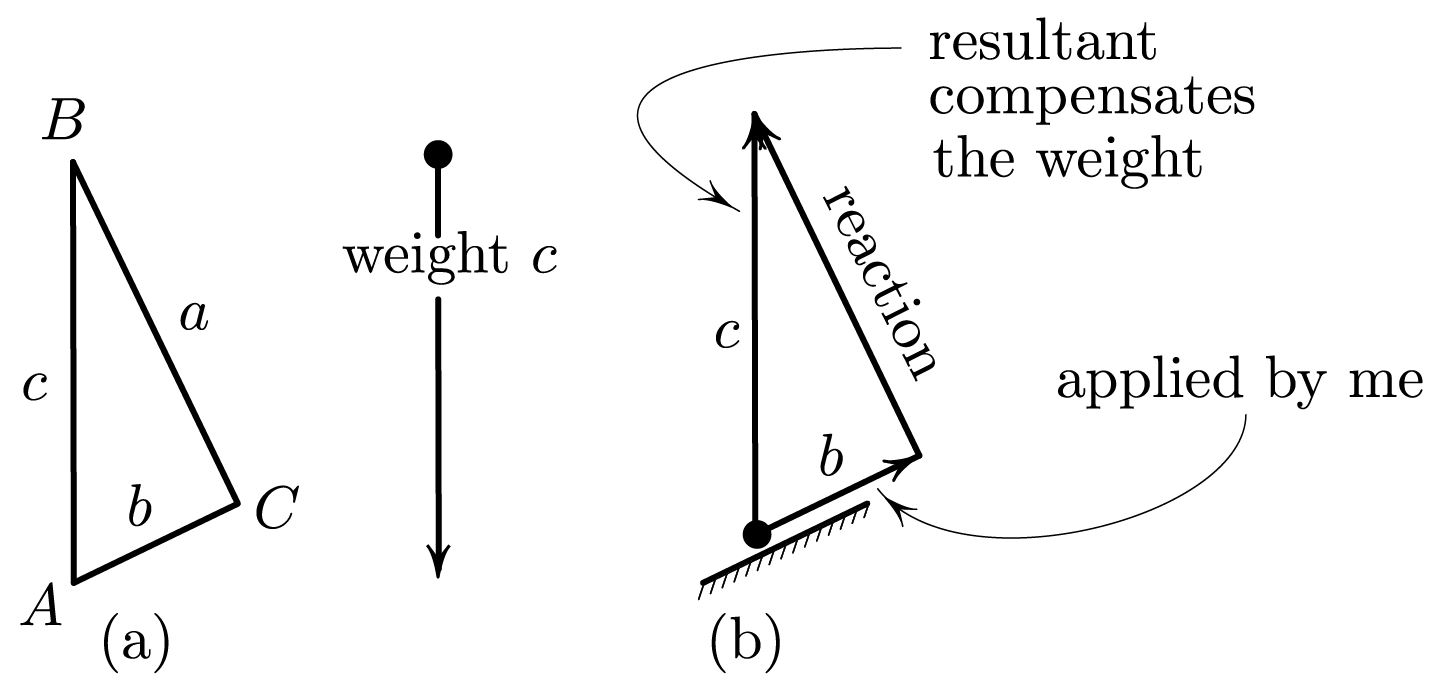
1. This physical “proof” of the Pythagorean theorem involves no work – mechanical work, that is. Figure 1a shows a right triangle, its hypotenuse held vertical. We take a point mass of the same weight c as the length of the hypotenuse,¹ so that \(c\) plays a double role of the length and of the weight. Lifting the mass along \(AB\) requires the same work as dragging it up the slippery ramps \(AC\) and \(CB\):

\[W_{AB}=W_{AC}+W_{CB}. \qquad (1)\]

Indeed, had the left-hand side been, say, smaller, we could have cycled the weight along the closed path \(ABCA,\) extracting more energy on the way down than we spent on the way up – a functioning perpetual motion machine.

Now \((1)\) gives the theorem, since \(W_{AB}=c\cdot c=c ^2,\) \(W_{AC}=b\cdot b = b ^2,\) and \(W_{CB}=a ^2,\) as explained by Figure 1 for \(W_{AC}.\) The Pythagorean theorem is thus one consequence of the constant vector field’s conservativeness.

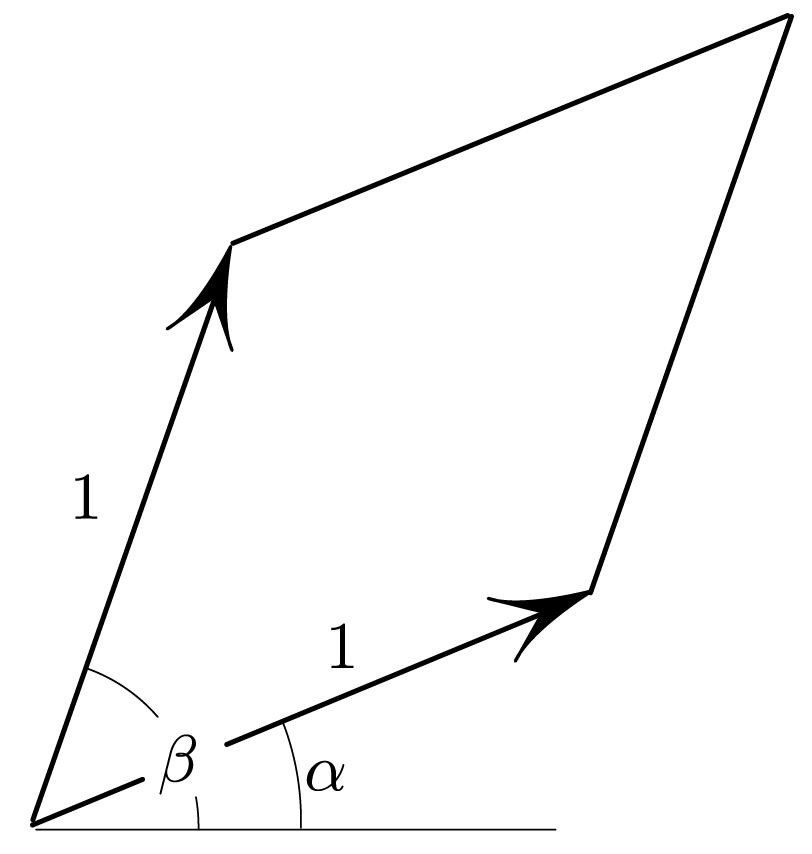
2. A wordless proof of the formula \(\sin (\beta - \alpha) = \sin \beta  \cos \alpha  - \sin \alpha \cos \beta,\) referring to Figure 2, expresses the same area in two different ways:

\[A=1\cdot 1\cdot \sin ( \beta   -\alpha   ) = \\ \\
\left|\begin{array}{cc} \cos   \alpha  & \cos  \beta   \\ \sin  \alpha   & \sin \beta  \end{array} \right| = \\ \\
\sin \beta \cos \alpha  - \sin \alpha\cos \beta.\]

All figures in the article are provided by the author.

¹ in some chosen units