Spinning Tops in Spinning Frames

Spinning tops have existed since ancient times. The popular toy is so old that it is difficult to say something simultaneously (i) new, (ii) correct, and (iii) interesting about it. The Lagrange top is an axisymmetric body that pivots on a needlepoint. When spun quickly enough, it precesses around the vertical axis while also possibly nutating.¹ In most books about classical mechanics [1, 3], the top is treated with somewhat lengthy calculations. Here I describe a point (pun intended) that is lost in standard treatments.

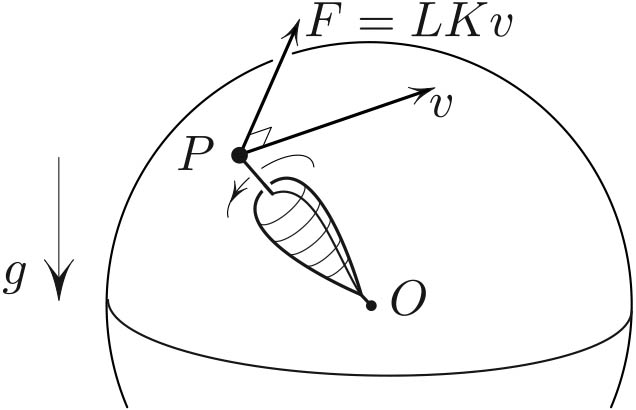
Let us keep track of the point \(P\) where the top’s axis punctures a sphere centered at \(O\) (see Figure 1). Dynamics of the top admit a remarkably simple description: 

The motion of \(P\) is identical to that of a point mass \(m\) constrained to the sphere of radius \(R\) and subject to two forces: (i) gravity and (ii) the (magnetic-like) force perpendicular to the velocity and of magnitude equal to the product of axial angular momentum \(L\), the Gaussian curvature \(K= R ^{-2}\) of the sphere and the velocity.

Both \(R\) and \(m\) are specified in terms of the top’s mass, moments of inertia, and the center of mass’ distance to the pivot; these expressions—as well as the claim’s proof—are available in [2]. The Lagrange top is thus equivalent to the charged particle on the sphere in the magnetic field that is perpendicular to the sphere (as if a magnetic monopole was at \(O\)) and subject to gravity. The strength of the magnetic field is given by the sphere’s Gaussian curvature, and the charge is the angular momentum \(L\).

Near-vertical Motions

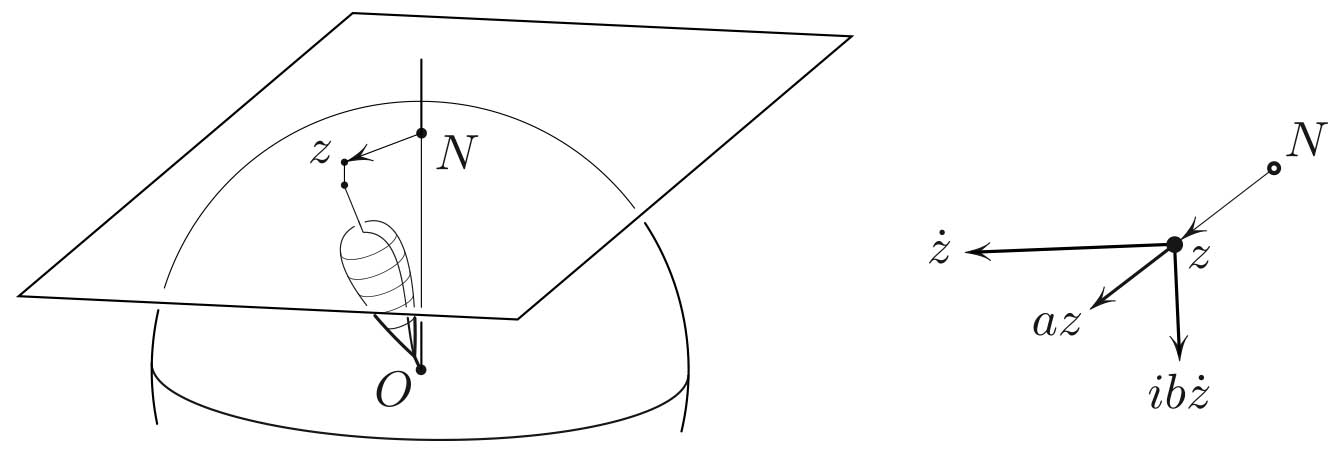
Figure 2 shows projection \(z=(x,y)=x+iy\) of \(P\) onto the tangent plane to the north pole. For near-vertical motions, \(z\) is a good approximation for \(P\) and it satisfies, up to higher order terms in \(|z|\), 

\[\ddot z =  ib \dot z+a z.\tag1\]

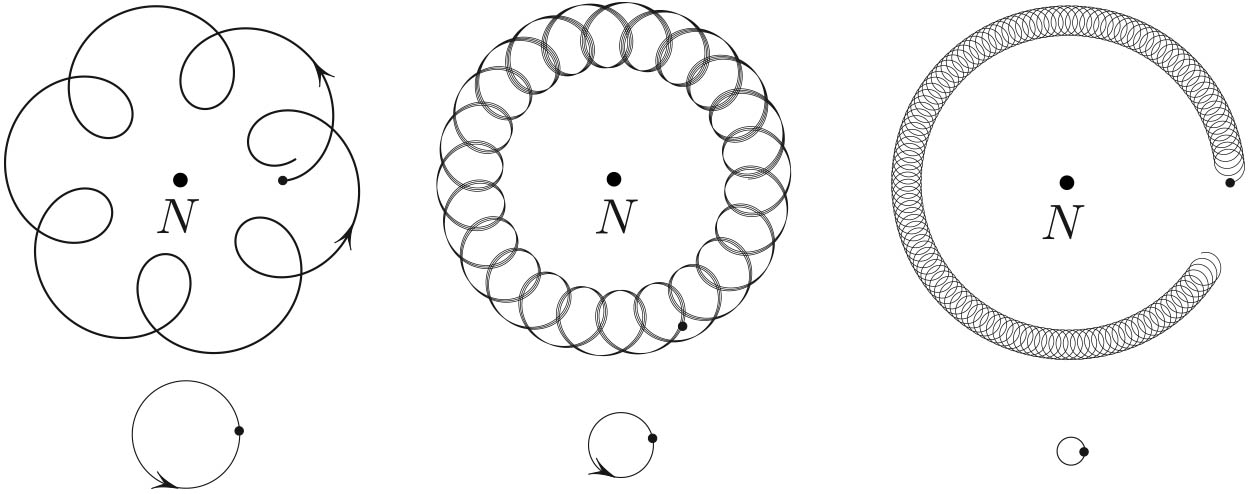
Here, \(a=g/R\) and \(b=LK/m\), although this is not important for the forthcoming point. Figure 3 shows typical trajectories of \(z\). Interestingly, when viewed in a rotating frame they are uniform circular motions — provided that we choose the right angular velocity for our frame. Indeed, any solution of \((1)\) is a combination of two circular motions:

\[z= A e^{i\omega_1t} +B e^{i\omega_2t},\tag2\]

where \(i \omega_1, \  i \omega_2\) are the roots of the characteristic polynomial \(\lambda ^2 -ib \lambda - a=0\). These roots are purely imaginary if \(b ^2 >4a\), which happens if the spin \(L\) is large enough (here, \(A\) and \(B\) are complex numbers). If we put ourselves in the frame that is rotating with angular velocity \(\omega_1\), then the motion \((2)\) will acquire a clockwise rotation from our point of view:

\[e^{-i\omega_1t}z = A + Be^{i(\omega_2- \omega _1)t}.\]

This rotation is a uniform circular motion centered at \(A\).

¹ “Nutus” = “nod” in Latin.

The figures in this article were provided by the author.

References

[1] Arnold, V.I. (1989). Mathematical methods of classical mechanics (2nd ed). In Graduate texts in mathematics. New York, NY: Springer-Verlag.
[2] Cox, G., & Levi, M. (2016). Gaussian curvature and gyroscopes. Comm. Pure Appl. Math., 71(5), 938-952.
[3] Goldstein, H. (1980). Classical mechanics. Reading, MA: Addison-Wesley.