Stochastic Rounding 2.0, With a View Towards Complexity Analysis

Stochastic rounding (SR) is a probabilistic rounding mode that is surprisingly effective in large-scale computations and low-precision arithmetic [3]. Its random nature promotes error cancellation rather than error accumulation, resulting in a slower growth of roundoff errors as the problem size increases — especially when compared to traditional deterministic rounding methods like rounding-to-nearest. Here, we advocate for SR as a foundational tool in the complexity analysis of algorithms and suggest several research directions.

Stochastic Rounding 1.0 

George Forsythe introduced SR in 1950 with a one-paragraph abstract for the 52nd meeting of the American Mathematical Society that was subsequently reprinted in SIAM Review [5]. In the context of numerical integration under rounding-to-nearest, Forsythe was concerned about modeling individual roundoff errors as random variables, as was first suggested by John von Neumann and Herman Goldstine in 1947. Forsythe observed that individual roundoff errors at times “had a biased distribution which caused unexpectedly large accumulations of the [total] rounding-off error,” and that “in the integration of smooth functions the ordinary rounding-off errors will frequently not be distributed like independent random variables” [5]. Hence Forsythe’s proposal of SR to make an individual roundoff error look like a “true random variable.”

Stochastic Rounding 2.0

Despite its illustrious beginnings, SR has since been largely overlooked by the numerical analysis community. Yet, the hardware design landscape exhibits a strong momentum towards SR implementations on graphics processing units (GPUs) and intelligence processing units (IPUs).

Commercial hardware—such as the Graphcore IPU, IBM floating-point adders and multipliers, AMD mixed-precision adders, and even NVIDIA’s implementations of deterministic rounding—already incorporate SR in various forms, as do Tesla D1 and Amazon Web Services Trainium chips. SR promotes efficient hardware integration and precision management, which are crucial for machine learning (ML) and artificial intelligence (AI). The advent of digital neuromorphic processors like Intel’s Loihi chip and SpiNNaker2, both of which feature SR, further underscores the readiness and even necessity of the widespread adoption of SR in hardware. The time is ripe for the adoption of SR as a standard feature in GPU and IPU architectures to optimize performance and accuracy across diverse applications.

Another reason to adopt SR is the emergence of deep neural networks (DNNs) and their implications for AI. Indeed, SR is primed to be a game-changer in training neural networks with low-precision arithmetic. It tends to avoid stagnation problems that are typical of traditional deterministic rounding modes, thereby allowing efficient training with minimal accuracy loss.

Prior work has demonstrated the successful training of DNNs on 16-bit and even 8-bit fixed-point arithmetic with SR, with the added benefit of significantly reducing energy costs. The performance of SR-based hardware compares favorably with that of higher-precision formats like binary32, but it comes with a lower computational overhead. SR’s application extends to dynamic fixed-point arithmetic and innovative hardware designs, such as in-memory computations and block floating-point numbers. SR has the ability to support training at various levels of arithmetic precision and enhance convergence speeds while maintaining training accuracy. These capabilities make it particularly attractive for AI applications, where computational efficiency and resource minimization are critical.

Our piece discusses challenges and opportunities for SR in numerical linear algebra. We propose SR as a model for algorithm complexity analysis that is natively implemented in hardware and discuss future research directions to alleviate its drawbacks.

SR Explained

Suppose we want to round the number \(0.7\) to a single bit: either \(0\) or \(1\). Traditional deterministic rounding-to-nearest rounds \(0.7\) to the nearest option, which is \(1\). In contrast, SR rounds \(0.7\) to \(1\) with probability \(0.7\) and to \(0\) with probability \(1-0.7=0.3\). The outcome of SR rounding is a random variable with expectation \(0.7\cdot 1 + 0.3\cdot 0 =0.7\). In statistical parlance, the rounded number is an unbiased estimator of the exact number. This simple statement has significant positive implications for the behavior of SR when analyzing the numerical accuracy of arithmetic operations.

The formal definition of the stochastically rounded version \(\textrm{SR}(x)\) of a real number \(x\) first appeared in [8]. Let \(\mathcal{F} \subset \mathbb{R}\) be a finite set of floating-point or fixed-point numbers, and assume that \(x\) is in the interval \([\min \mathcal{F}, \max \mathcal{F}]\). Identify the two adjacent numbers in \(\mathcal{F}\) that bracket \(x\):

\[\lceil\!\lceil{x}\rceil\!\rceil = \min \{y \in \mathcal{F}: y \geq x\} \quad \text{and}\quad \lfloor\!\lfloor{x}\rfloor\!\rfloor = \max \{y \in \mathcal{F}: y \leq x\}.\tag1\]

Thus, \(\lfloor\!\lfloor{x}\rfloor\!\rfloor\leq x\leq \lceil\!\lceil{x}\rceil\!\rceil\). If \(\lfloor\!\lfloor{x}\rfloor\!\rfloor=\lceil\!\lceil{x}\rceil\!\rceil\), then \(\textrm{SR}(x)=x\). Otherwise, SR rounds with higher probability to the closer of the two numbers:

\[\textrm{SR}(x) = \begin{cases}\lceil\!\lceil{x}\rceil\!\rceil & 
\textrm{with probability}\ p(x)\equiv \frac{x - \lfloor\!\lfloor{x}\rfloor\!\rfloor}{\lceil\!\lceil{x}\rceil\!\rceil  - \lfloor\!\lfloor{x}\rfloor\!\rfloor},\\ 
\lfloor\!\lfloor{x}\rfloor\!\rfloor & \textrm{with probability}\ 1-p(x)
\end{cases}\]

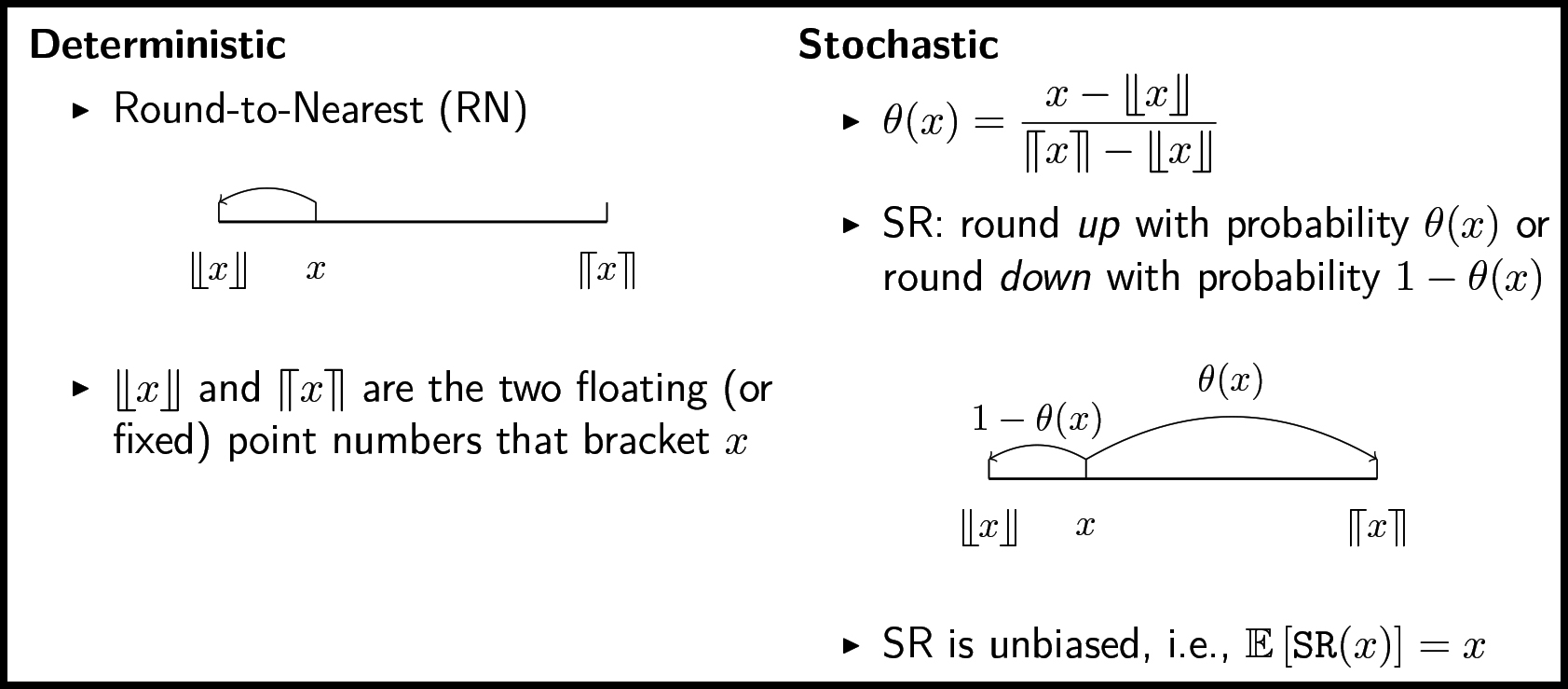
(see Figure 1). An alternative is the SR up-or-down mode [3, 10], where rounding up or down happens independently of \(x\) with probability \(p(x)=1/2\).

Advantages of SR

Early SR work [7] described probabilistic models for roundoff error analysis and concluded that such models are generally very good in both theory and practice. The recent renaissance of SR makes a strong case for randomization in the rounding process:

• SR produces roundoff errors with zero mean, thereby encouraging cancellation (rather than accumulation) of errors. In contrast, rounding-to-nearest can accumulate large roundoff errors whenever the individual errors have the same sign.
• SR tends to avoid stagnation. This phenomenon is associated with rounding-to-nearest [2, 3], where many tiny updates to a large quantity get lost in the rounding process. Suppose that we want to compute the sum \(s_0+\Sigma_{j=1}^k{s_j}\), where \(s_0\in\mathcal{F}\) and the magnitude of the summands \(|s_j|\) is sufficiently small compared to \(|s_0|\) (i.e., smaller than half of the distance from \(s_0\) to the closest numbers in \(\mathcal{F}\)). Then the rounding-to-nearest operation \(\textrm{fl}(\cdot)\) produces \(\textrm{fl}(s_0+\Sigma_{j=1}^k{s_j})=s_0\). This means that the addition of \(s_j\) does not change the sum, and the sum stagnates.
• The total roundoff error from SR tends to grow more slowly with the problem size than the one from rounding-to-nearest. Specifically, the total roundoff error from the summation of \(n\) numbers under SR has, with high probability, a bound proportional to \(\sqrt{n}u\), where \(u\) is the unit roundoff [6]. This is in contrast to rounding-to-nearest, where the bound is proportional to \(nu\). The proofs in [6] rely on measure of concentration inequalities for sums of random variables—such as Bernstein, Chernoff, and Hoeffding inequalities—and corroborate the bound empirically.
• SR increases the smallest singular value of tall-and-thin matrices, thereby improving their conditioning for the solution of least squares/regression problems. We demonstrated [4] that SR implicitly regularizes such matrices in theory and practice, therefore improving their behavior in downstream ML and data analysis applications. Our proofs rely on non-asymptotic random matrix theory results, which unfortunately lack tightness and intuition.

Limitations of SR

Here we summarize several drawbacks of SR when compared to rounding-to-nearest:

• Lack of reproducibility: SR introduces randomness in rounding decisions, leading to nondeterministic results across different runs of the same computation.
• Inability to use true randomness: Because implementing SR with true randomness is impossible, one must resort to pseudorandom number generators (PRNGs). This creates an additional layer of complexity in both theoretical analysis and practical applications.
• Increased computational overhead: SR requires additional computational resources to generate pseudorandom numbers and perform the rounding operation, which can slow performance.
• Limited adoption in legacy systems: Existing numerical libraries and systems may not be able to support SR, limiting its adoption in legacy codes and applications. A detailed discussion of SR implementations in hardware and software is available in [3].

Our Proposal: SR for Complexity Analysis

The most ambitious research agenda for SR, from a numerical linear algebra and theoretical computer science perspective, is the opportunity to establish a complexity analysis of algorithms in its presence.

Existing methodologies for assessing the performance of algorithms include the following four. Worst-case analysis upper bounds the maximum time (or space) that an algorithm could possibly require, thus ensuring performance guarantees in even the most challenging scenarios. Average-case analysis assesses expected performance over a distribution of all possible inputs and offers a measure of efficiency for typical cases. Amortized analysis evaluates the average performance of each operation in a sequence and spreads the cost of expensive operations over many cheaper ones, ultimately providing a balanced perspective of overall efficiency. And smoothed complexity, introduced in the early 2000s, aims to bridge the gap between worst- and average-case analyses by evaluating algorithm performance under slight Gaussian random perturbations of worst-case inputs [9], thus reflecting practical scenarios where inputs are not perfectly adversarial. Smoothed complexity has gained significant recognition for its profound impact on the analysis of algorithms. Its importance is underscored by prestigious awards, including the 2008 Gödel Prize, 2009 Delbert Ray Fulkerson Prize, and 2010 Rolf Nevanlinna Prize.

In contrast, we propose the use of complexity analysis under SR to analyze the performance of algorithms whose operations are performed with SR. The small, random perturbations that are inflicted by each SR operation should, one hopes, move algorithms away from worst-case instances. In this sense, complexity analysis under SR is reminiscent of smoothed complexity but has the major advantage of being natively implemented in modern hardware, which accurately reflects algorithm performance in silico. Therefore, SR complexity analysis is a potentially viable and realistic alternative to worst-case and smoothed analysis because it offers a comprehensive understanding of algorithmic behavior on modern hardware.

We envision several research directions to exploit the unique advantages of SR as a foundation for complexity analysis. First, there is a need for a theoretical framework that can rigorously define and evaluate the effect of SR on algorithm performance. A straightforward initial approach could consist of a perturbation analysis of SR’s impact when applied solely to the original input, with computations in exact arithmetic. This approach parallels smoothed complexity analysis, but a more advanced framework would also evaluate the influence of SR on computations within the algorithm.

Second, it is crucial to establish empirical benchmarks and compare SR to traditional deterministic rounding modes across a wide range of real-world applications. Doing so would help understand its practical benefits and limitations, particularly for computations on large-scale data sets in low-precision arithmetic (e.g., ML and AI applications). These research directions could solidify SR’s role as a foundational tool in complexity analysis — akin to the role of smoothed complexity in bridging theoretical and practical perspectives in algorithm performance assessment.

Other Research Directions for SR

Finally, we urge the scientific community to focus on the following research directions. 

• Reproducibility in the context of SR requires the employment of PRNGs with fixed seeds. While PRNGs are not truly random, they offer a well-studied, repeatable source of randomness [1]. As such, the design of PRNGs that balance performance and randomness quality and are optimized for hardware integration would be particularly useful. SR could also be selectively applied in critical parts of the algorithm or on inputs that are far from rounding boundaries. More precisely, SR could be selectively employed for inputs \(x\) that deviate significantly from \(\lfloor\!\lfloor{x}\rfloor\!\rfloor\) and \(\lceil\!\lceil{x}\rceil\!\rceil\), as these cases result in larger perturbations and a more pronounced impact on the outcome.
• The development of practical non-asymptotic random matrix theory tools could significantly enhance our knowledge of SR’s behavior in numerical linear algebra computations. User-friendly bounds for SR would allow for a better understanding of the effect of SR on standard numerical algorithms and could lead to proofs that SR is a potent approach to reducing error propagation and increasing numerical accuracy. 
• A gradual integration of SR into widely-used numerical libraries and standards—combined with clear guidelines and tools for the adaption of legacy systems—could help its incorporation into existing software libraries without the need for extensive rewrites.

References
[1] Barker, E.B., & Kelsey, J.M. (2015). Recommendation for random number generation using deterministic random bit generators. Special publication (NIST SP) 800-90A rev. 1. Gaithersburg, MD: National Institute of Standards and Technology.
[2] Connolly, M.P., Higham, N.J., & Mary, T. (2021). Stochastic rounding and its probabilistic backward error analysis. SIAM J. Sci. Comput., 43(1), A566-A585.
[3] Croci, M., Fasi, M., Higham, N.J., Mary, T., & Mikaitis, M. (2022). Stochastic rounding: Implementation, error analysis and applications. R. Soc. Open Sci., 9(3), 211631.
[4] Dexter, G., Boutsikas, C., Ma, L., Ipsen, I.C.F., & Drineas, P. (2024). Stochastic rounding implicitly regularizes tall-and-thin matrices. Preprint, arXiv:2403.12278.
[5] Forsythe, G.E. (1959). Reprint of a note on rounding-off errors. SIAM Rev., 1(1), 66-67.
[6] Hallman, E., & Ipsen, I.C.F. (2023). Precision-aware deterministic and probabilistic error bounds for floating point summation. Numer. Math., 155(1-2), 83-119.
[7] Hull, T.E., & Swenson, J.R. (1966). Tests of probabilistic models for propagation of roundoff errors. Commun. ACM, 9(2), 108-113.
[8] Parker, D.S. (1997). Monte Carlo arithmetic: Exploiting randomness in floating-point arithmetic. Los Angeles, CA: University of California, Los Angeles.
[9] Spielman, D., & Teng, S.-H. (2001). Smoothed analysis of algorithms. In STOC ’01: Proceedings of the thirty-third annual ACM symposium on theory of computing (pp. 296-305). Hersonissos, Greece: Association for Computing Machinery.
[10] Vignes, J. (2004). Discrete stochastic arithmetic for validating results of numerical software. Numer. Algorithms, 37, 377-390.