Stressing Microbes to Create Macroscopic Patterns

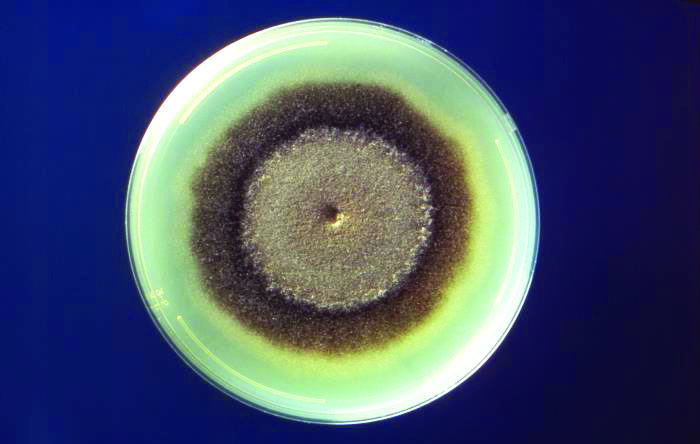
Microbes in Petri dishes often grow in distinctive circular or wavelike patterns that are visible even without a microscope (see Figure 1). These growth formations develop without any long-range communication between individual cells, which means that they arise from microscopic mechanical and biochemical interactions rather than environmental factors. External forces—e.g., the borders of the Petri dish, added chemicals, or fluid properties of the growth medium—affect the macroscopic patterns in unique ways.

To understand the emergence of collective growth patterns, one must draw connections between several factors across a range of length scales. Computational biologists, mathematicians, and biomedical engineers use numerical simulation techniques to model the way in which idealized bacteria form macroscopic patterns simply from the stresses that they exert on each other as they grow and multiply [2]. “You have a cell that grows and divides, grows and divides,” Scott Weady of the Flatiron Institute’s Center for Computational Biology said. “How does a bacterium that slows its growth in response to pressure influence the global mechanics of the colony?”

It is difficult to dynamically measure individual cell size and growth in a lab, and functionally impossible to measure the mechanical stresses that each microbe imposes on its neighbors. To further complicate the situation, microbes in these environments are tightly packed, with effectively no empty space between them. This arrangement results in a nonlinear problem wherein the growth of each simulated “bacterium” is inhibited by its neighbors, while the bacteria’s own existence simultaneously exerts stress on those same neighbors. Solving this problem necessitates the use of mathematical methods that were developed for grain packing and computer graphics, as well as techniques from the branch of applied math known as active matter. Weady and his collaborators constructed a macroscopic fluid model that is controlled by parameters from the microscopic simulations, and ultimately reproduced the familiar circular growth patterns of microbe cultures.

Packing ‘Em In

Modeling efforts in ordinary granular matter research frequently seek to identify the arrangement of grains with fixed shapes and sizes under gravity or other constraints. Scientists often approximate microbes like E. coli bacteria or certain types of yeast as sphero-cylinders: capsule-like shapes consisting of spheres that are sliced in half, with a cylinder of the same diameter inserted between the halves.

The growth of these “grains” introduces a new type of stipulation, in addition to simple restrictions that the particles cannot overlap; now, models must also include the stress that each microbe places on its neighbors (and vice versa). This stress inhibits the allowable growth of individual cells within the boundaries of the microbial colony, eventually producing the aforementioned concentric macroscopic growth patterns.

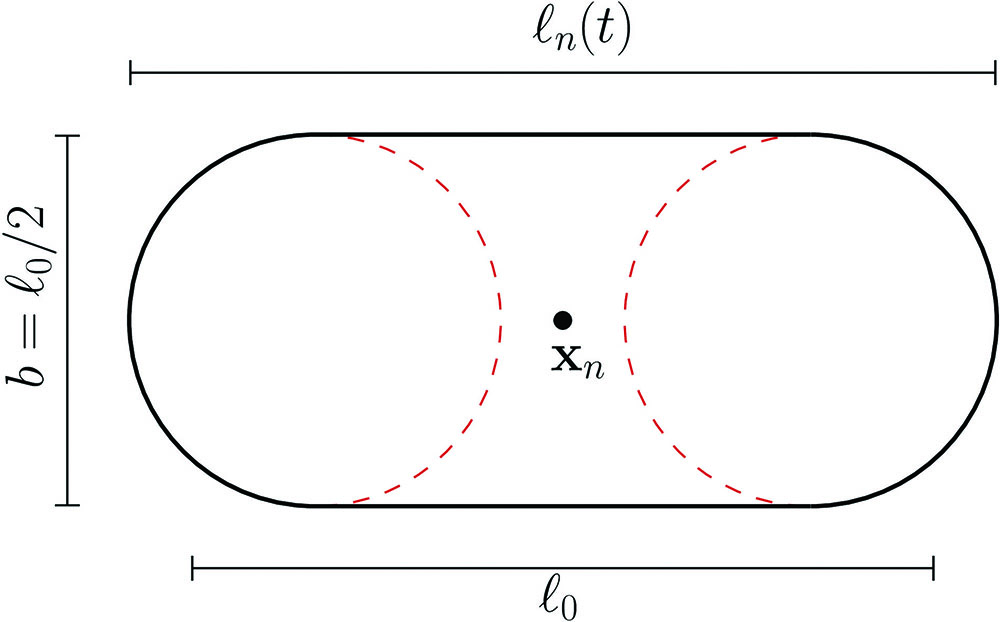
The simplified model involves a set of \(N\) sphero-cylinders with constant diameter \(b\) (see Figure 2). Each microbe \(n\) increases in length from \(\ell_0=2b\) at an exponential rate \(\tau\) that is moderated by the contact stress \(\lambda\sigma_n\) exerted by its neighbors:

\[\frac{d\ell_n}{dt}=\frac{\ell_n}{\tau}\exp(-\lambda\sigma_n).\]

Once a microbe reaches a length of \(2\ell_0\), it divides into identical sphero-cylinders and the process repeats. The microbes only move and rotate under the influence of contact forces \(\mathbf{F}_n\) and torques \(T_n\) from their neighbors:

\[\frac{d \mathbf{x}_n}{dt}=\frac{\mathbf{F}_n}{\xi\ell_n} \quad \textrm{and} \quad \frac{d\theta_n}{dt}=\frac{12}{\xi\ell^3_n}T_n.\]

Here, \(\xi\) is a friction constant due to the substrate beneath the microbes, \(\mathbf{x}_n\) is the position of the center of mass, and \(\theta_n\) is the orientation.

The result is a nonlinear optimization problem that requires an effective solution for the entire colony. Even when disregarding food supply and other external factors, this non-Newtonian problem does not have ordinary action-reaction forces. “From a modeling perspective, you no longer have conservation laws,” Weady said. “So you have to think about non-conservation.”

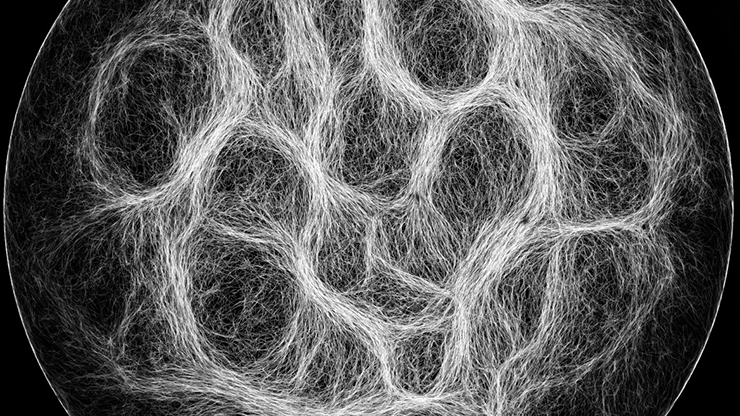
The simulation—which begins with one microbe—is governed by a single free parameter \(\lambda'=(\tau/\xi\ell^2_0)\lambda\) (scaled to be dimensionless) that characterizes sensitivity to stress from neighboring microbes. Running the simulation until the colony reaches a maximum size of \(R=150\ell_0\) reveals emergent concentric growth patterns that qualitatively correspond to those in Petri dishes.

Waves Without Waves

While these particle simulation results certainly look compelling, it is hard to check the microscopic picture against reality. Measuring the growth and division rates for microbial colonies is difficult, and tracking movement, rotation, and stress for huge numbers of organisms is impractical at best. To connect the microscopic view with measurable macroscopic quantities, Weady and his colleagues formulated a set of continuum fluid equations based on an existing model that researchers often use to describe microbe growth. “Our insight was to bridge two different modeling strategies that have existed for a long time in a new, satisfying way,” Weady said. Philosophically, this approach is much like how condensed matter physicists utilize computationally challenging multi-particle quantum calculations to find equations that describe bulk material properties.

The relevant collective properties for this scenario are ambient fluid pressure \(p\) and flow velocity \(\mathbf{u}\) (as opposed to internal forces, stresses, and torques on individual cells). To model microbe growth and division, the researchers employ a growth flux field that is parameterized by the same stress sensitivity \(\lambda\) as in the particle simulations. Since the microbes do not orient themselves preferentially along any axis in the absence of external forces, the macroscopic model assumes rotational isotropy and treats pressure simply as a function of position and time.

The fluid model equations—analogous to the microscopic force equations—are

\[\xi \mathbf{u} + \nabla p=0 \quad \textrm{and} \quad \nabla \cdot \mathbf{u}=(1/\tau)e^{-\lambda p},\]

where pressure vanishes at the colony’s boundary. For equivalent stress sensitivity values \(\lambda'\), the solutions to these fluid equations produce very similar patterns to the microscopic simulations (see Figure 3). Although these patterns might closely resemble waves, the fluid model indicates a clear distinction.

“They look a lot like waves and move a lot like waves, but based on the [mathematical] solution, they’re not really waves,” Weady said. “Some cells [experience] more stress over their lifetime, and some experience less. The cumulative process of resistance to growth happens all the time — there’s no wave pattern to that. The cells feel more or less stress depending on where they are, and that persists, accumulates, and gets passed on from generation to generation.”

New Ways to Stress Microbes

Despite the obvious applications to laboratory biology, Weady admitted that his group’s primary motivation was curiosity. “We did simulations and saw this [thing] that was kind of cool,” he said. “Let’s try and understand it. That’s what we do as theoretical applied mathematicians, but it’s a concrete prediction that can be tested.”

For precisely this reason, an important next step will be some simple laboratory experiments on E. coli — though Weady and his collaborators are interested in extending the math to additional scenarios as well. Weady specified that the simulations and models are already three dimensional; they were only restricted to flat surfaces for the investigation’s first iteration in order to match laboratory settings.

Immediate extensions to this mathematical work will involve examinations of the interactions between two microbe populations, the effect of surface properties—such as a liquid substrate—on a single population’s growth, and overall growth over a curved surface [1]. “Microbes often colonize ships, or something like that,” Weady said. “I’m interested in putting [microbes] in different environments with different curvatures and [seeing] how stress sensing might relate to curvature sensing, and how it affects spread over a surface.”

While this research might be driven by curiosity, its applications could inspire a deeper knowledge of real-world systems — potentially even those that do not concern microbes. As such, the connection between simple stresses on colony growth and macroscopic patterns has profound implications for our mathematical understanding of the propagation of structures across relatively wide distances in the absence of communication.

References
[1] Francis, M. (2023, November 1). Wildebeest self-organization via active matter theory. SIAM News, 56(9), p. 12.
[2] Weady, S., Palmer, B., Lamson, A., Kim, T., Farhadifar, R., & Shelley, M.J. (2024). Mechanics and morphology of proliferating cell collectives with self-inhibiting growth. Phys. Rev. Lett., 133(15), 158402.