Successes, Collaborations, and Forward Momentum for Inverse Problems in Finland

Inverse problems, which seek to interpret indirect measurements of an unknown, arise in multiple contexts. Examples include deblurring an out-of-focus photograph, deducing Earth’s internal structure based on earthquake data, imaging with radar and sonar, and finding the optimal shape of a structural component. Curiously, research in this field tends to concentrate on the most vicious cases, where the inversion task (from effect to cause) is much more sensitive to errors than the direct process (from cause to effect). It’s as if the mathematical inversion community is intentionally looking for trouble!

Nevertheless, inverse problems do offer an extensive playground for mathematicians. The field makes use of a variety of mathematical tools, such as functional analysis, geometry, harmonic analysis, numerical linear algebra, complex analysis, and Bayesian statistics. Within SIAM, inversion researchers often find a home in the Activity Groups (SIAGs) on Imaging Science, Computational Science and Engineering, Data Science, Geosciences, and Uncertainty Quantification.

Considering the multitude of hubs for inversion scientists, let me mention the country of Finland. While this Northern European nation has only 13 universities and a humble population of 5.5 million, it is home to 19 professors of inverse problems and a vibrant community of students, postdoctoral researchers, visitors, and end users of mathematical algorithms. Many of us are long-term SIAM members, and some are quite active in conference organization and other SIAM activities. For instance, Tanja Tarvainen of the University of Eastern Finland was a member of the Organizing Committee for the 2022 SIAM Conference on Uncertainty Quantification (UQ22) and 2024 SIAM Conference on Imaging Science (IS24); Tapio Helin of Lappeenranta-Lahti University of Technology (LUT) served on the 2024 SIAM Conference on Uncertainty Quantitation Organizing Committee; Heikki Haario of LUT co-chaired UQ22; and I co-chaired IS24, served as program coordinator for the SIAG on Imaging Science (SIAG/IS) in 2022 and 2023, and was previously the SIAM News liaison for SIAG/IS — I’ve even written for SIAM News [5]. How did the modest country of Finland become so involved in the inverse problems sphere?

The mathematics of inverse problems is wonderful in many ways, but its main claim to fame is in the connection between pure research and practical applications. The Finnish inverse problems community has seriously invested in this aspect for more than 30 years. Partial overlaps between different areas of expertise enable the step-by-step—or rather, scholar-by-scholar—transfer of ideas all the way from theory to practice. And the reverse is also true, as applied work with real data always brings unexpected challenges that in turn raise new scientific questions. One such example is the development of a three-dimensional (3D) dental X-ray device from an inherently two-dimensional panoramic dental imager [3]; this problem arose from customer needs at the Finnish company Instrumentarium (later acquired by GE HealthCare).

Due to the strong alignment between Finnish inversion activity and national research and innovation strategies, the Research Council of Finland has provided continuous Centres of Excellence funding for inverse problems since 2006. And as part of its Flagship Programme, the Research Council launched the Flagship of Advanced Mathematics for Sensing, Imaging and Modelling (FAME) in 2024. This multidisciplinary center aims to accelerate the transfer of scientific ideas to the service of industry and society through cutting-edge research on inverse problems. Science education and outreach to general audiences are also central to FAME.

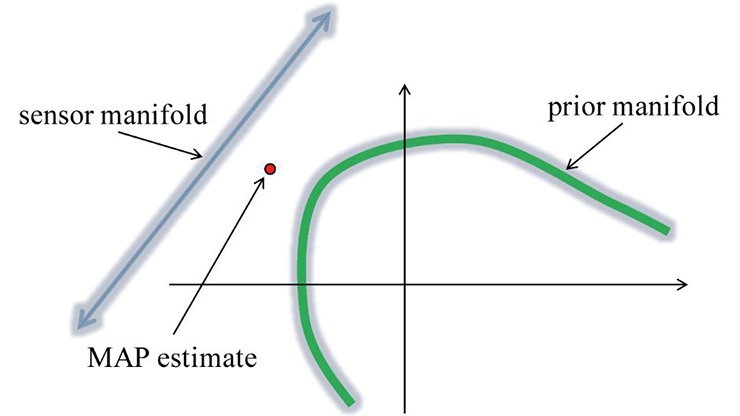
Two examples of applied research that embody FAME’s mission are satellite remote sensing and electrical impedance tomography (EIT). First, satellites have revolutionized our ability to receive information from all parts of the globe. The observation of greenhouse gases from space is a particular point of interest, and several space agencies and even commercial companies have built and launched satellites (see Figure 1) that measure backscattered solar light in the shortwave infrared wavelength region. These measurements detect the concentration of carbon dioxide and methane, which can derive emissions that are closely linked to climate change.

National greenhouse gas reporting, as outlined in the Paris Agreement, is based on models of societal activities like fossil fuel consumption. Complementary observation-based estimates come from local (at city or powerplant scales) or global satellite measurements of greenhouse gas concentrations. All of these steps—from a satellite’s detection of scattered photons to the verification of emission reductions—require the solution of inverse problems. Science-based climate policy relies on such estimates, preferably in conjunction with transparent uncertainty quantification. This is a key goal of FAME.

Recently, our team at the Finnish Meteorological Institute (FMI) used satellite data to develop emission estimation methods [6]. This work is motivated by the European Space Agency’s upcoming Copernicus Anthropogenic Carbon Dioxide Monitoring mission (see Figure 1), which will use air quality observations to fundamentally improve global monitoring of carbon dioxide and methane from space [4]. Our methodological breakthroughs in the interpretation of satellite data stem from a history of idea exchange between FMI researchers and pure mathematicians that has led to several new algorithms, such as adaptive Markov chain Monte Carlo [2] and an open-source MATLAB toolbox.

Moving on, EIT is an imaging modality wherein electrodes that are attached to a surface feed electric currents into a patient or another target. Using measurements of the resulting voltages, the goal is to form an image of the distribution of internal electric conductivity. The Finnish inverse problems community began contributing to EIT in the early 1990s, driven by the pioneering work of Erkki Somersalo (now at Case Western Reserve University); since then, Finns have produced many theoretical advances and various computational algorithms in this discipline.

One industrial EIT success story is the birth of Numcore. Founded in 2008 to pioneer innovative 3D imaging solutions for the process industry, this startup company in Kuopio, Finland, was acquired by Outotec—a minerals and metal processing technology heavyweight that is now part of Metso—just four years later.

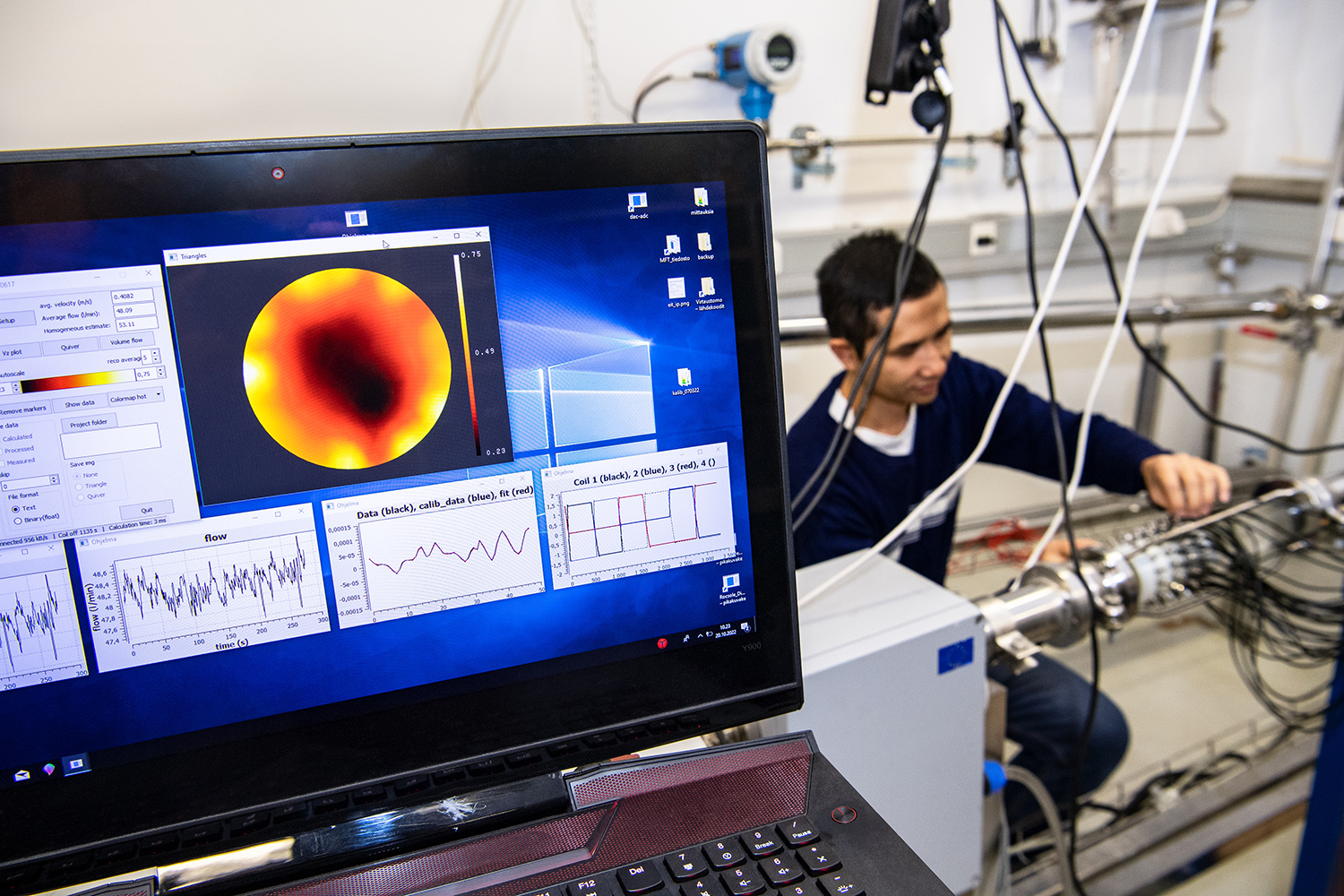
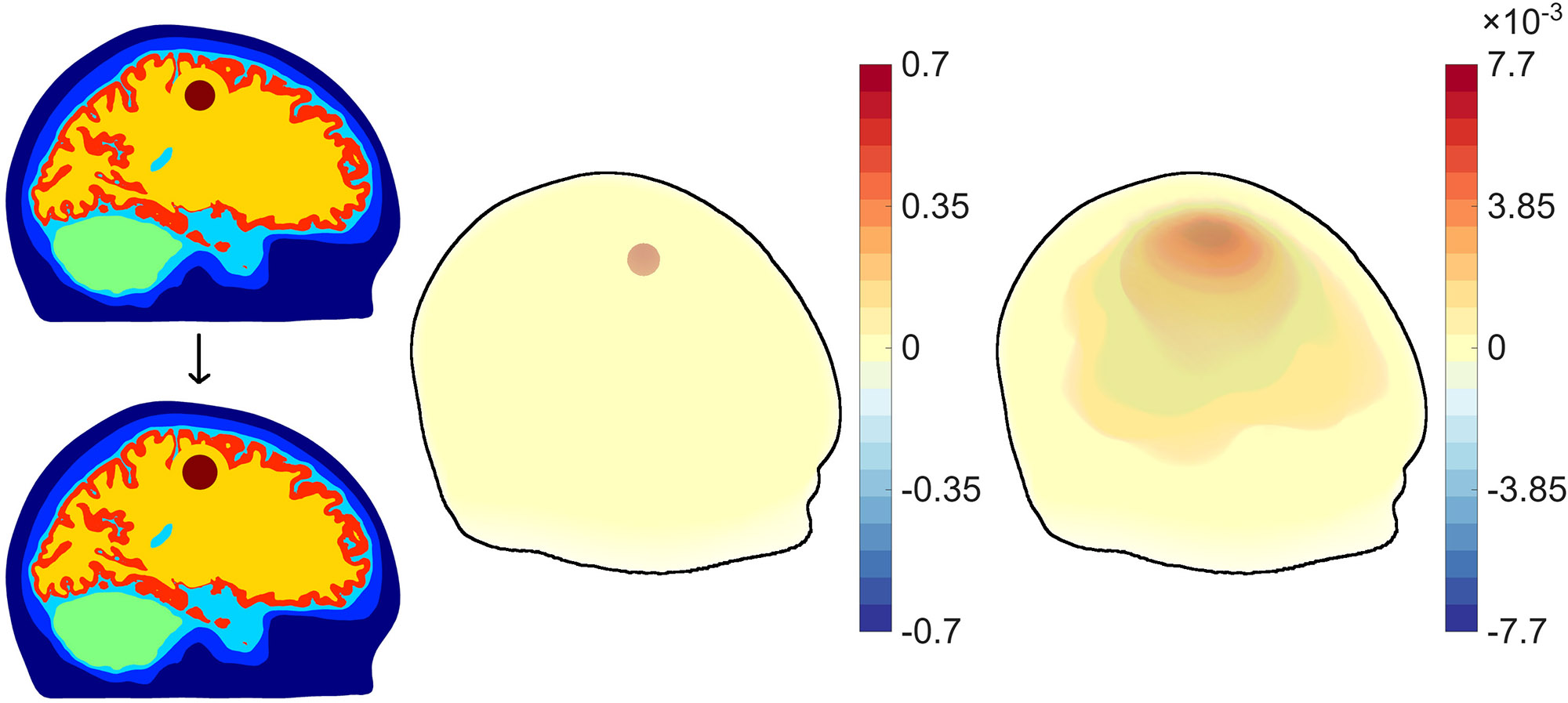
Researchers at six FAME sites are currently studying EIT by quantifying the uncertainty in electrode locations, finding the optimal scalar conductivity reconstruction for EIT from an anisotropic target, exploring invisibility cloaking possibilities for new materials with exotic properties, and designing hybrid classical/artificial intelligence algorithms. Additionally, an ongoing intensive study is investigating the use of EIT to diagnose and monitor strokes (see Figure 2) [8]. FAME scholars are actively developing EIT for several industrial applications — e.g., to monitor the health of concrete structures, quantify the moisture transport properties of cement-based materials [7], and measure multiphase flows in the process industry (see Figure 3) [1]. Open-source EIT software packages like Object Oriented Electrical Impedance Tomography, as well as open datasets—such as the dataset from the Kuopio Tomography Challenge 2023—are freely available online.

As we approach the Finnish Inverse Problems Society’s 30th annual Inverse Days conference, which will take place from December 10-13, the future of Finland’s inverse problems community looks bright. With the Research Council’s substantial long-term support, FAME can focus on the collaborative development of novel methodologies and technological solutions in areas such as healthcare, health technologies, clean energy, and component manufacturing.

At the same time, the Doctoral Education Pilot for Mathematics of Sensing, Imaging and Modelling—part of the Ministry of Education and Culture’s initiative to introduce new practices in graduate education—will train 100 developing inverse problems experts across seven Finnish universities in the next few years. FAME will work closely with the Doctoral Education Pilot to ensure that the high-quality scientific and industry-driven training will help to realize the full potential of the next generation of inverse problems scientists.

Acknowledgments: The author would like to acknowledge Hannakaisa Lindqvist and Johanna Tamminen of the Finnish Meteorological Institute; Ville Kolehmainen, Aku Seppanen, Tanja Tarvainen, and Marko Vauhkonen of the University of Eastern Finland; and Mikko Helenius of Aalto University for their contributions to this article.

References 
[1] Arif, M.Z., Seppänen, A., Kolehmainen, V., & Vauhkonen, M. (2023). Dual-modal electrical imaging of two-phase flow – Experimental evaluation of the state estimation approach. Sensors, 23(9), 4462. 
[2] Haario, H., Saksman, E., & Tamminen, J. (2001). An adaptive Metropolis algorithm. Bernoulli, 7(2), 223-242. 
[3] Kolehmainen, V., Vanne, A., Siltanen, S., Järvenpää, S., Kaipio, J.P., Lassas, M., & Kalke, M. (2007). Bayesian inversion method for 3D dental X-ray imaging. Elektrotech. Infotech., 124(7-8), 248-253. 
[4] Meijer, Y., Andersson, E., Boesch, H., Dubovik, O., Houweling, S., Landgraf, J., … Lindqvist, H. (2023). Anthropogenic emission monitoring with the Copernicus CO2 monitoring mission. Front. Remote Sens., 4, 1217568. 
[5] Samuli, S. (2012, June 1). Probing the deep mathematics of nonlinear inverse problems. SIAM News, 45(5), p. 4.
[6] Santaren, D., Hakkarainen, J., Kuhlmann, G., Koene, E., Chevallier, F., Ialongo, I., … Broquet, G. (2024). Benchmarking data-driven inversion methods for the estimation of local CO₂ emissions from XCO₂ and NO₂ satellite images. Atmos. Meas. Tech., to appear. 
[7] Smyl, D., Hallaji, M., Seppänen, A., & Pour-Ghaz, M. (2016). Three-dimensional electrical impedance tomography to monitor unsaturated moisture ingress in cement-based materials. Transp. Porous Media, 115(1), 101-124. 
[8] Toivanen, J., Paldanius, A., Dekdouk, B., Candiani, V., Hänninen, A., Savolainen, T., … Kolehmainen, V. (2024). Simulation-based feasibility study of monitoring of intracerebral hemorrhages and detection of secondary hemorrhages using electrical impedance tomography. J. Med. Imaging, 11(1), 014502.