Surrogate-model-based Bayesian Estimation of Alto Guadalentı́n Aquifer Properties
The Alto Guadalentín region in Southeast Spain is an inland valley that is dedicated to crop production (see Figure 1a). Between the early 1960s and the late 1980s, intensive groundwater extraction for agricultural purposes lowered the underlying aquifer water table by more than 100 meters. This action led to a phenomenon known as land subsidence, i.e., a gradual sinking of the ground. The land subsidence rate in this area is actually one of the largest in Europe; the ground descended by about 15 centimeters per year between 1992 and 2007, for a total downward movement of approximately three meters.
Surprisingly, this phenomenon went unnoticed for years and was first reported in 2011 [3]. It has not caused any major infrastructural damage thus far, likely because the Guadalentín Basin is mostly rural. Although recent years have seen less water extraction, the situation remains critical because aquifer recharge is very limited; the basin experiences a semi-arid climate with sporadic rainfall, and the aquifer’s only primary inflows are seasonal watercourses. It is therefore imperative that further land subsidence is mitigated by establishing future groundwater exploitation policies based on reliable predictions of the aquifer’s mechanical response to water pumping.
![<strong>Figure 1.</strong> Graphical illustration of some of the findings of our work. <strong>1a.</strong> Location of the Alto Guadalentín valley and the three-dimensional simulated domain; colors represent the land elevation in meters above mean sea level. <strong>1b.</strong> Computed land subsidence rate of the Guadalentín Basin for the maximum <em>a posteriori</em> value of uncertain parameters in 1992, 2004, and 2016. Figure 1a courtesy of [4] and 1b courtesy of the authors.](/media/ihlbxcqe/figure1.jpg)
In our recent work [4], we present an uncertainty quantification framework for this very context. More specifically, we consider a state-of-the-art mathematical model of the aquifer system’s hydro-mechanical behavior and use a surrogate-model-based Bayesian approach to determine the posterior distribution of the model’s parameters according to available system measurements — i.e., to calibrate the value of these parameters and estimate their residual uncertainties. The final result is a tool that can match available data and provide data-informed land subsidence predictions with uncertainty ranges. To the best of our knowledge, this is one of only a few attempts in the literature to embed a highly nonlinear mathematical model of an aquifer in an uncertainty quantification framework at basin scale over a multi-decadal period.
Our mathematical model consists of two coupled, nonlinear partial differential equations. The first is a variation of Richards’ equation, which describes the flow of water in a porous medium that is subject to variable saturation and mechanical deformation. The second is a classical mechanical equilibrium equation that (i) accounts for the effect of pore pressure variation—caused by water flow—on mechanical stress (Terzaghi’s principle), and (ii) incorporates the partial recovery of deformation due to such pressure variations (mechanical hysteresis). This latter equation is responsible for the computation of land subsidence [5].
The Guadalentín Basin is roughly contained within a 25-kilometer-by-12-kilometer-by-50-meter box, with a well-studied lithological structure [2]. For the purposes of our study, this structure was simplified to four units: clay, sand, silt, and rock. To achieve reasonable accuracy when solving the associated system of equations, the computational mesh must comprise about one million tetrahedra, with element sizes that range from a few meters to approximately one kilometer depending on the lithological unit. Furthermore, we employ a staggered time-marching scheme that covers the period from 1972 to 2016, with time steps on the order of days — such that one simulation takes approximately three days.
Two kinds of data are available to calibrate the mathematical model. The first type consists of piezometric records from Confederación Hidrográfica del Segura (the local water management authority), which were pre-processed by the Geological and Mining Institute of Spain; these data include measurements from nine wells between 1972 and 1988 and six wells between 1988 and 2012 [1]. The second type of data comprises land surface displacement observations from five Interferometric Synthetic Aperture Radar (InSAR) datasets from 1992 to 2016 [2]. Unfortunately, the piezometric records contain various data gaps and the measurements’ accuracy is unknown, which somewhat limits the efficacy of the calibration procedure.
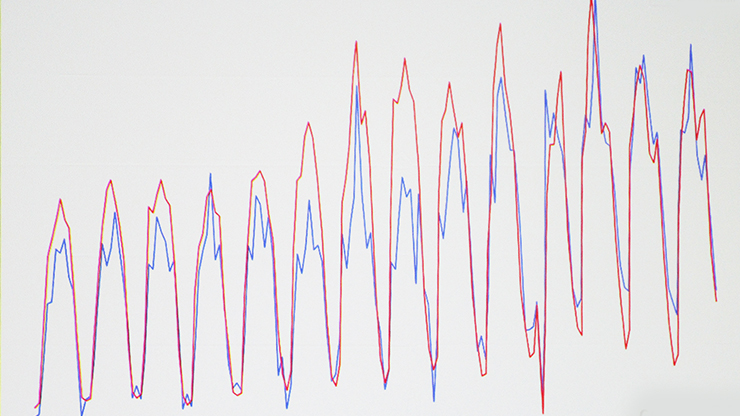
![<strong>Figure 2.</strong> Comparison between computed values of subsidence rate (where the orange line is simulated values and the green shade is the 2.5-97.5 percentile range) and measured values from Interferometric Synthetic Aperture Radar (InSAR) (blue line) for 2012 at 39 different locations in the Guadalentín Basin. Subsidence rate (vz) is measured in centimeters per year (cm/year). Figure adapted from [4].](/media/xzkjmu20/figure2.jpg)
As is typical with this kind of application, many model parameters are uncertain in principle, such as initial conditions, lithological unit properties, and historical aquifer discharge/recharge rates. However, the temporal and spatial scales of the simulation and the modest quality of the piezometric records force us to limit the number of parameters to be tuned with the Bayesian calibration procedure, and instead focus on reproducing only the aquifer’s macroscopic trends. More specifically, based on geophysical/engineering considerations, we decided to calibrate two parameters: (i) the horizontal hydraulic conductivity of the sandy lithological unit \((K_s)\) and (ii) the parameter that controls the elastic behavior of the clayey lithological unit \((c_{mc}).\) Both parameters remain constant throughout their units, which keeps the complexity to a minimum.
We utilized a classical Bayesian approach to perform parameter calibration—specifically, we employed slice sampling Markov chain Monte Carlo [6] to explore the posterior of uncertain parameters—with two caveats. First, we could not use direct simulations of the aquifer to obtain evaluations of the likelihood function due to the large computational time of a single simulation. We therefore replaced direct simulations with sparse-grid surrogate models [7]. Second, the finite element solver fails to converge for low values of \(K_s\) and high values of \(c_{mc}\), which would lead to non-physically large drawdown in the clayey layer. As such, it was not possible to train a global surrogate model on the parametric domain.
However, the same nature of the available data for calibration suggests a remedy. We performed a preliminary calibration of just \(K_s\) against the piezometric data from 1972 to 1988, assuming no land subsidence in those years (which means that we only used a surrogate for the groundwater equation). The calibration yielded an intermediate posterior for \(K_s\), which ruled out the values that were causing issues with solver convergence. We then conducted a second calibration for both parameters that yielded satisfactory results.
With this setup, the calibrated model demonstrated good agreement with the data, given the limitations of the aforementioned data quality. Figure 1b illustrates the temporal evolution of the Guadalentín Basin’s predicted land subsidence for the maximum a posteriori value of the uncertain parameters, and Figure 2 shows the agreement between predictions and InSAR data at different locations within the basin.
Ultimately, we believe that researchers can utilize this prediction tool to design effective future water management policies for the Guadalentín Basin.
Lorenzo Tamellini delivered a minisymposium presentation on this research at the 2025 SIAM Conference on Computational Science and Engineering, which took place in Fort Worth, Texas, this past March.
Acknowledgments: Lorenzo Tamellini was partially supported by the PRIN 2022 PNRR project “Uncertainty Quantification of Coupled Models for Water Flow and Contaminant Transport” (P2022LXLYY), which was financed by the European Union’s (EU) NextGenerationEU. Chiara Piazzola acknowledges support from the Alexander von Humboldt Foundation. Yueting Li and Claudia Zoccarato acknowledge support from the RESERVOIR project (sustainable groundwater RESources managEment by integrating eaRth observation deriVed monitoring and flOw modelIng Results), which is funded by the Partnership for Research and Innovation in the Mediterranean Area program supported by the EU (grant agreement 1924).
References
[1] Cerón García, J.C. (1995). Estudio hidrogeoquímico del acuífero del Alto Guadalentín (Murcia). [Ph.D. dissertation, Departamento de Geodinámica, Universidad de Granada]. Retrieved from https://digibug.ugr.es/handle/10481/55814.
[2] Ezquerro, P., Guardiola-Albert, C., Herrera, G., Fernández-Merodo, J.A., Béjar-Pizarro, M., & Bonì, R. (2017). Groundwater and subsidence modeling combining geological and multi-satellite SAR data over the Alto Guadalentín aquifer (SE Spain). Geofluids, 2017(1), 359325.
[3] González, P.J., & Fernández, J. (2011). Drought-driven transient aquifer compaction imaged using multitemporal satellite radar interferometry. Geology, 39(6), 551-554.
[4] Li, Y., Zoccarato, C., Piazzola, C., Tamellini, L., Bru, G., Guardiola-Albert, C., & Teatini, P. (2025). Characterizing aquifer properties through a sparse grids-based Bayesian framework and InSAR measurements: A basin-scale application to Alto Guadalentı́n, Spain. Water Resour. Res., 61(8), e2024WR038543.
[5] Nardean, S., Ferronato, M., Zhang, Y., Ye, S., Gong, X., & Teatini, P. (2021). Understanding ground rupture due to groundwater overpumping by a large lab experiment and advanced numerical modeling. Water Resour. Res., 57(3), e2020WR027553.
[6] Neal, R.M. (2003). Slice sampling. Ann. Statist., 31(3), 705-767.
[7] Piazzola, C., & Tamellini, L. (2024). Algorithm 1040: The sparse grids Matlab kit — a Matlab implementation of sparse grids for high-dimensional function approximation and uncertainty quantification. ACM Trans. Math. Softw., 50(1), 7.
About the Authors
Lorenzo Tamellini
Senior researcher, Italian National Research Council
Lorenzo Tamellini is a senior researcher at the Institute of Applied Mathematics and Information Technologies of the Italian National Research Council. His research focuses on several aspects of uncertainty quantification, including single- and multi-fidelity surrogate modeling construction, sensitivity analysis, Bayesian inversion, applications in science and engineering, and software.

Yueting Li
Postdoctoral researcher, Nanjing University
Yueting Li is a postdoctoral researcher in the Department of Hydrosciences within the School of Earth Sciences and Engineering at Nanjing University in China. Her research focuses on land subsidence, numerical modeling, surrogate modeling, and uncertainty quantification.

Chiara Piazzola
Postdoctoral researcher, Technical University of Munich
Chiara Piazzola is a postdoctoral researcher in the Department of Mathematics at the Technical University of Munich in Germany. Her research addresses different aspects of uncertainty quantification (e.g., surrogate modeling, sensitivity analysis, and Bayesian inversion), with a particular focus on dynamical systems applications.

Claudia Zoccarato
Postdoctoral researcher, University of Padova
Claudia Zoccarato is a Marie Skłodowska-Curie postdoctoral researcher in the Department of Civil, Environmental, and Architectural Engineering at the University of Padova in Italy and a visiting scholar in the Department of Earth Sciences at the University of Delaware. Her research focuses on numerical modeling of land subsidence by natural and human-induced factors, including uncertainty quantification and Bayesian estimation.

Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.