swMATH: A Publication-based Approach to Mathematical Software
The growing importance of mathematical software in everyday life—in applications such as internet communication, traffic, and artificial intelligence—necessitates advances in software documentation services to raise awareness of existing packages and their usage. Such information helps potential software developers and users make informed choices about packages that could advance their work in modeling, simulation, and analysis. At the same time, software presents novel challenges to information services that require the development of new methods and means of processing.
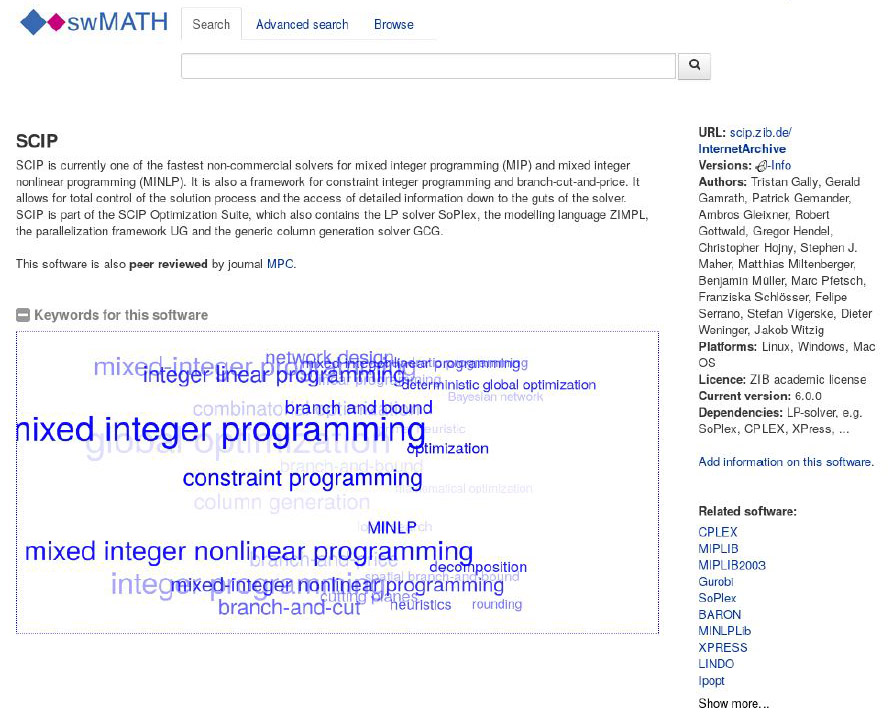
swMATH provides users with an overview of a broad range of mathematical software and extends documentation services for publications related to such software (see Figure 1). It acts as a counterpart to the established abstracting and reviewing services for mathematical publications and has nearly 30,000 entries, making it one of the most comprehensive documentation services in mathematics.
A Publication-based Approach
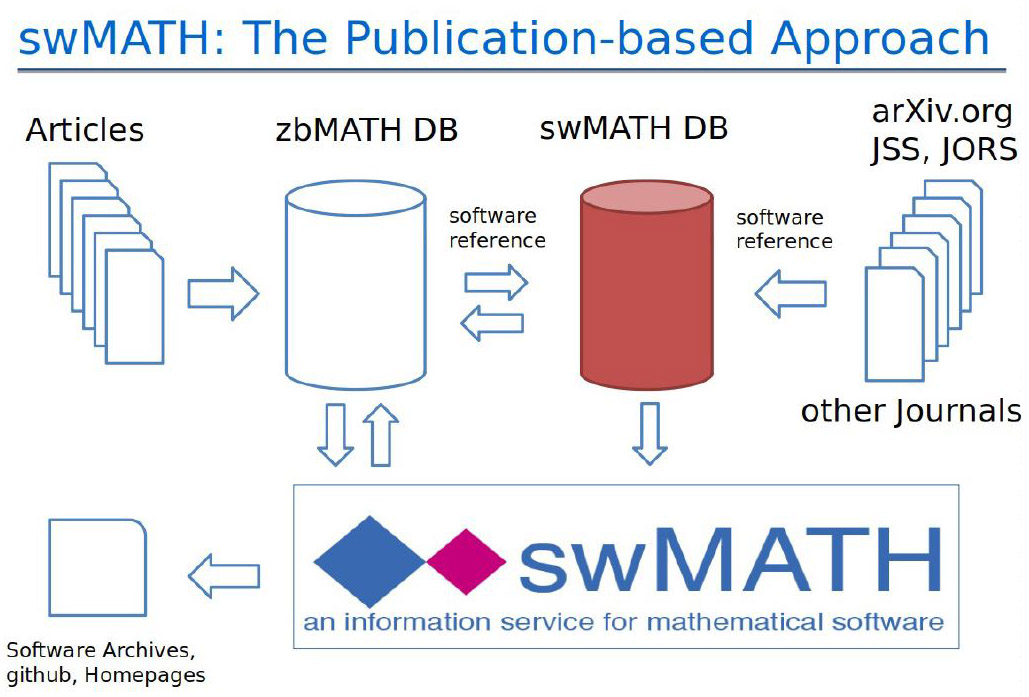
swMATH employs a so-called publication-based approach that essentially extracts information about software from existing mathematical literature for documentation purposes (see Figure 2). Publications tend to feature two types of software information. On one hand, they contain descriptions of software and provide details about the problem classes, algorithms, and test results. On the other hand, they offer data on software usage and its application areas and findings. swMATH conducts analysis by differentiating between publications that focus on software descriptions (standard publications) and uses (user publications). For example, a search for “integer programming” yields a list of software that includes SCIP, Gurobi, and CPLEX (see Figure 1).
The publication-based approach is successful because a growing number of scientific articles describe or cite mathematical software; for example, swMATH currently has 382,778 software references in 205,487 different articles. Many publications specialize in algorithms and mathematical software, and their analyses yield a great deal of information. As indicated by the aforementioned use of heuristic procedures, the publication-based method is largely automatic. However, accessing the mathematical literature continues to be a major challenge. Large bibliographic databases in mathematics—such as Mathematical Reviews and zbMATH—offer nearly complete and systematic overviews of mathematical publications, beginning in 1868 and 1940 respectively. These databases include reviews, abstracts, keywords, citation lists, and/or mathematical classifications. The data is available in structured form and thus allows for a field-based evaluation.
swMATH adopts heuristic methods—in particular, analysis of characteristic word patterns and art words that are often used as software names—to evaluate zbMATH entries (which will be open access as of 2021). Searching titles and citations is particularly effective. One of swMATH’s main features is its ability to link software with the citing literature. Publication metadata in zbMATH entries helps derive a variety of directly and indirectly extracted software metadata.
In the case of directly derived metadata, software descriptions entail a review or abstract of standard publications. Keywords in standard publications characterize the mathematical area, background, and keywords of the referenced user publications. The Mathematics Subject Classification code of standard or user publications uniformly assigns mathematical and application areas. After all, publications that cite software comprise metadata that deliver contextual references and contact persons.
For indirectly derived metadata, the relationship between swMATH entries and citations indicates that a software is quoted more than 10 times on average, but the citation numbers are very different. High citation numbers indicate software acceptance and can be considered a metric of quality. Publication data provide information about the software’s developmental state. Finally, common citations in zbMATH entries point to similarity or dependency relationships between software artifacts.
Development of Software Documentation Services
Software documentation services must address the needs of both developers and users. Developers often wish to leverage existing software for collaboration or extend its capabilities with further development. And users require software to solve problems of interest, which necessitates the availability of source code, application programming interfaces (APIs), documentation, and user experience information. Users must also have the ability to discover existing software that addresses particular problem classes (integer programming, for example).
A variety of mathematical software information services meet these various needs, including services like GitHub that provide software development environments, especially code development; software archives such as Software Heritage that permanently archive software artifacts; and software documentation services like Wikipedia or software catalogs of user groups.
Accepting Mathematical Software in swMATH
The evaluation of software quality depends on many factors—including correctness, development level, user interface, support, hardware and software dependencies, and licenses—that are also influenced by user perspectives. The swMATH database is limited to entries from distinguished sources that help to ensure software quality:
- Entries extracted from zbMATH citations: The publication-based approach ensures that swMATH includes software artifacts cited in the zbMATH database. zbMATH evaluates only peer-reviewed publications, which particularly applies to publication results that are achieved using software. The citation is an indirect indicator of the software’s acceptance and subsequent quality. The same applies in principle to entries that result from evaluation of the arXiv repository.
- Entries obtained from software journals: Journals specializing in scientific software, like ACM Transactions on Mathematical Software or Mathematical Programming Computation, also increasingly include verification of reported results.
- Entries from software repositories: Software repositories, such as the Comprehensive R Archive Network repository for statistical software, have special requirements for inclusion. These stipulations in turn provide indirect statements about an entry’s quality.
Enrichment
One can utilize swMATH entries to link software with related detailed information, including the website, code, or API. Popular software often have their own URLs, though these links are not always permanent. Therefore, swMATH entries link to websites as well as scans of websites that are available in the Internet Archive.
Developer platforms like GitHub are frequently used in the academic sector for distributed creation and further development. These platforms typically provide access to the latest versions of software but do not permanently secure previous software artifacts. Software Heritage has built an archive of software artifacts in recent years that periodically mirror, store, and share all freely available information from key developer platforms. swMATH cooperates with Software Heritage and connects entries to the available software artifacts.
By linking to software websites, the Internet Archive, and Software Heritage, swMATH offers much more than a list of existing mathematical software. Rather, it is a portal for mathematical software that accommodates the needs of various user groups. Nevertheless, the swMATH resource must be further expanded and developed. The publication-based approach means that swMATH entries are subject to delays caused by the publishing process. As a result, other sources—such as the arXiv and mathematical software publications—are included in the evaluation. Data analysis should thus be extended to as many journals as possible. The user interface also enables manual entry of additional information. Furthermore, the portal allows one to embed software in its mathematical context, e.g., by connecting algorithms with possible software implementations. Researchers are currently discussing an extension of the approach that involves linking with algorithms and test data, which seems realistic.
About the Authors
Wolfgang Dalitz
Scientist, Zuse Institute Berlin
Wolfgang Dalitz is a scientist at Zuse Institute Berlin who works in the field of scientific information systems. He has been involved in building mathematical software libraries since the late 1980s.
Wolfram Sperber
Editor, Zentralblatt für Mathematik
Wolfram Sperber has been editor of Zentralblatt für Mathematik since 2006. He retired from his position as a senior researcher at FIZ Karlsruhe in 2019.
Hagen Chrapary
Software Developer, Zentralblatt
Hagen Chrapary is a software developer at Zentralblatt and Zuse Institute Berlin.
Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



