Teaching Numerical Linear Algebra Online
The COVID-19 pandemic’s sudden arrival forced on-campus classes to go virtual practically overnight. At the time, we were in the midst of the first offering of a graduate-level online course on numerical linear algebra (NLA)—titled “Advanced Linear Algebra for Computing”—for the Master of Computer Science Online (MCSO) program at the University of Texas at Austin. The MCSO program is partnered with edX, a nonprofit that provides massive open online courses (MOOCs). For this course, we created a set of materials that we call "Advanced Linear Algebra: Foundations to Frontiers" (ALAFF); we were also using ALAFF for an on-campus version of the same course and a MOOC on edX. Because we had specifically designed our materials for online learning—building on five years of experience developing three previous MOOCs—we were in better shape than many of our colleagues when all courses transitioned to an online-only format. Here we describe our efforts and their motivations.
One primary advantage of an online course is flexibility. An online format can target learners with different background experiences, learning styles and paces, and overall goals; building course material around this format thus greatly impacts the learning experience. Those who teach graduate-level NLA have likely encountered diverse audiences that include mathematicians, computer scientists, engineers, and domain scientists. NLA therefore benefits from the adaptability of online course material.
Like a traditional course, an effective online course incorporates lectures, readings, exercises, activities, discussions, and assessments. The benefit of an online format is that we can orchestrate these different components as easy-to-consume chunks that are interleaved to encourage “minds-on” engagement. Students can choose when, how, and in what order they access this content, depending on their learning styles and circumstances. For example, one learner may wish to watch all the videos and then move on to exercises. Another may dive straight into the exercises and consult the videos only when they need the instructor’s perspective. This adaptable format puts students in control of their engagement with the material.
Professors can also use scaffolded exercises to guide participants’ development of their own knowledge, understanding, skills, and fluency. Releasing new materials on a schedule and setting deadlines for completion encourages progress through the virtual course. Much like in-person classes, the goal of online instruction is to construct an active learning environment wherein an instructor, aided by the materials, guides the discovery of knowledge instead of simply feeding information to the learners.
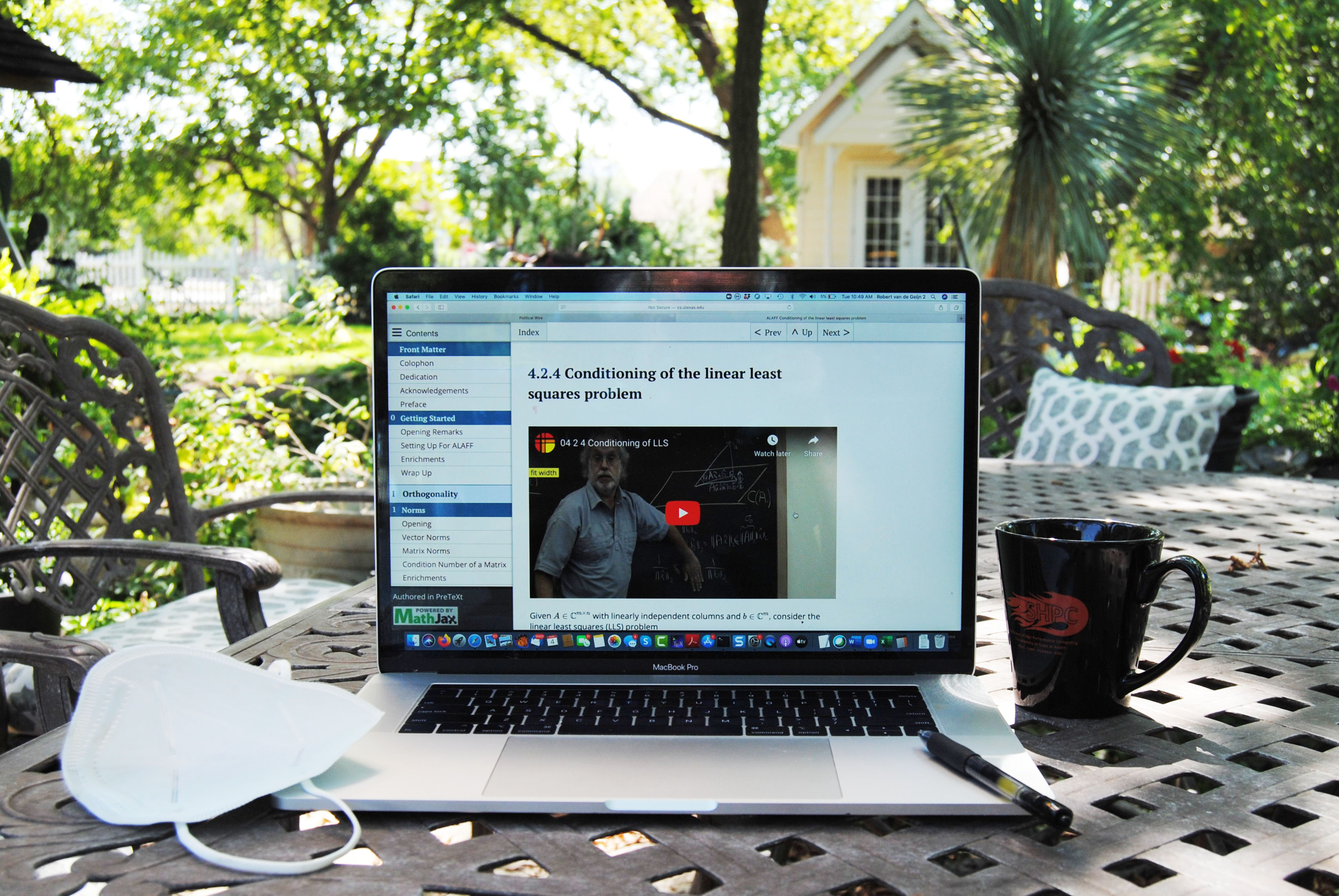
When deciding how to flexibly provide a rich set of components, materials, and options without overwhelming the learner, the choice of authoring tool is key. We recently discovered the PreTeXt authoring tool, which produces an electronic book as a set of webpages and optionally as a PDF. YouTube videos are embedded in the online version, the PDF includes hyperlinks to these videos, and a paper copy of the PDF provides access with QR codes. The look and feel of the PreTeXt webpages ensure that students are not inundated with too much information at once. A navigation bar provides an overview of the document’s contents and organization, and users can remove clutter by exposing or hiding information on demand. For instance, proofs of theorems, hints, answers, and/or (multiple) full solutions for exercises are only exposed upon student request. Additional hyperlinks conveniently direct users to related topics. In other words, the document exploits the richness that webpages afford.
How did we translate this into a virtual NLA course? So as not to overwhelm students, we took the traditional topics of an NLA course and organized them into three parts: orthogonality, linear systems, and the algebraic eigenvalue problem. We introduced orthogonality first—including a treatment of norms, orthogonal spaces, the Singular Value Decomposition, and the solution of linear least squares problems—because it involves prerequisite knowledge for other courses that students often pursue in parallel with (or even before) NLA. Each part comprised four weeks and concluded with an assessment. Every week began with an “opener,” which engaged learners in an activity that motivated the week’s topic and established learning objectives that provided an a priori checklist of topics for mastery. A combination of videos, text, activities, and exercises guided students towards proficiency throughout the week, which ended with a summary of key insights. Prior to each summary, enrichments provided context and linked to recent advances in NLA, including our own research.
This format seemed to work well for participants. “This class really demonstrates how actually building a course around an online format can make a huge difference in the learning experience,” one student said.
We have thus far described ALAFF, a freely available resource that takes the place of a traditional text and can be used independently as such. Students in our on-campus version of the NLA course during the spring of 2020 interacted in the classroom, during office hours, and on Piazza (an online question-and-answer platform) until the course went virtual due to COVID-19. We wanted to maintain a similar level of engagement with the 60+ students who had signed up for the online course. Our team accomplished this by communicating with students via a combination of the edX discussion forum, Canvas (a learning management platform), and Zoom (a popular video conference platform). As primary instructors, we personally answered questions on the discussion forums in a timely manner.
One student identified instructor feedback on assignments and exams, active professor communication and participation in discussions, and excellent organization of course material as the most effective aspects of the online experience. Another spoke highly of the interactive components. “I had concerns regarding the online platform of this program,” the student said. “However, I am very impressed by how fast [instructors] respond to questions posted on the discussion board. The active interaction makes me feel like I am not studying alone and I’m not isolated.”
We also built homework assignments and assessments that focused on active learning. These included take-home-style exams containing some programming assignments that involved back-and-forth communication with students. Exams and homework feedback were not part of the MOOC experience, which only incorporates self-assessments. One of our learners praised the exam style. “I thought that was the best final I’ve ever experienced,” the student said. “I got hands-on experience implementing an algorithm to finally compute the Singular Value Decomposition, which we had been building towards all semester, and I learned about a cool factorization technique to compute eigenvectors even faster. Getting the chance to ask questions and actually learn from exam problems was a breath of fresh air.”
The insights in this article stemmed from our experience creating and running other MOOCs, all of which are offered on edX. We began in 2013, when we were funded by the University of Texas System to create “Linear Algebra: Foundations to Frontiers” (LAFF): a full-semester undergraduate introduction to linear algebra. “LAFF-On Programming for Correctness” is a six-week course that shares our techniques for systematic discovery of families of algorithms for matrix operations, from which one can choose the best (e.g., highest-performing) in context. “LAFF-On Programming for High Performance” is a four-week course that employs matrix-matrix multiplication to illustrate fundamental techniques for high performance on modern central processing units. These courses dovetail with ALAFF. A self-assessment (pretest) of preparedness for ALAFF points those who require a review of basic linear algebra to LAFF content. Some ALAFF enrichments address topics for which the other two MOOCs provide more in-depth study. Thus, our four MOOCs collectively offer a loosely coupled experience.
The ultimate takeaway of these courses is that effective and high-quality online education at the undergraduate and graduate level is certainly feasible. Institutions will likely see more courses of this nature in the coming semesters.
Acknowledgments: Development of the various MOOCs was supported in part by National Science Foundation awards ACI-1148125, ACI-1550493, CCF-1714091, and CSSI-2003921. Additional funding came from the University of Texas System, MathWorks, and a HornRaiser crowdfunding campaign.
About the Authors
Robert van de Geijn
Faculty member, The University of Texas at Austin
Robert van de Geijn is a faculty member at The University of Texas at Austin who is affiliated with the Department of Computer Science and the Oden Institute for Computational Engineering and Sciences. He received his Ph.D. in applied mathematics from the University of Maryland and is a leading expert in the areas of high-performance computing, linear algebra libraries, and parallel processing.
Maggie Myers
Senior Research Fellow, Oden Institute for Computational Engineering and Sciences
Maggie Myers is a Senior Research Fellow at the Oden Institute for Computational Engineering and Sciences at The University of Texas at Austin. She holds a Ph.D. in mathematical statistics from the University of Maryland and has extensive experience developing educational materials for K-12, college, and graduate-level courses.
Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



