Ten Memorable Planar Curves and Their Remarkable Histories

Curves for the Mathematically Curious: An Anthology of the Unpredictable, Historical, Beautiful, and Romantic. By Julian Havil. Princeton University Press, Princeton, NJ, October 2019. 280 pages, $29.95.

Eight years ago, Ian Stewart published In Pursuit of the Unknown: 17 Equations That Changed the World. The book—along with an associated wall poster that displayed the 17 equations—was very popular with a large audience of math enthusiasts. Books consisting of vignettes that pertain to one particular category date back to at least 1851, with Edward Creasy’s The Fifteen Decisive Battles of the World: From Marathon to Waterloo. The genre has become extremely popular in recent years, as the framework provides a handy, flexible organizational structure for both the writer and reader. The field of computer science has Nine Algorithms that Changed the Future: The Ingenious Ideas That Drive Today’s Computers by John MacCormick. General history has titles like A History of the World in 12 Maps by Jerry Brotton, A History of the World in 100 Objects by Neil MacGregor, and the Smithsonian’s History of the World in 1,000 Objects; indeed, authors have penned histories in 100 objects about women, the Tudors, Ireland, American sports, the Third Reich, and so forth.

Julian Havil’s newest book—Curves for the Mathematically Curious: An Anthology of the Unpredictable, Historical, Beautiful, and Romantic—follows this pattern and illuminates episodes in the history of mathematics with 10 curves: the Euler spiral, the continuous but nowhere differentiable Weierstrass function, Bezier curves (i.e., cubic splines), the rectangular hyperbola, the quadratrix of Hippias, space-filling curves, constant-width curves, the normal curve, the catenary, and elliptic curves. Havil is a retired former master at Winchester College, an elite public school in Hampshire, England.

The book contains a great deal of valuable mathematics and mathematical history. I personally found the chapter on the Euler spiral—with its beautiful equation “curvature = arc length”—particularly satisfying from a geometric viewpoint. And the backstories of the normal curve (from Abraham de Moivre to Carl Friedrich Gauss) and the space-filling curve (from Georg Cantor and Richard Dedekind to Giuseppe Peano and David Hilbert) offered fascinating historical insight.

However, readers must prepare to work; Havil does not coddle them. He immediately gets down to business in the second paragraph of chapter one: The standard practice of expressing a curve in parametric form \(x=g(t)\), \(y=h(t)\) brings with it variants of formulae for its common characteristics: its slope, the area under it, its arc length, and its curvature. This sentiment essentially sets the tone for the book as a whole.

For the most part, the mathematical toolbox upon which Havil relies is remarkably limited and mainly consists of high school geometry, algebra, trigonometry, and calculus. For instance, the chapter about the normal curve calls for a minimal amount of probability theory. Polar coordinates, vectors, geometric transformations, three-dimensional geometry, non-Euclidean geometry, and projective geometry go entirely unmentioned. Complex numbers appear only a few times in passing. Havil uses matrices to abbreviate systems of linear equations but not for any geometric purposes. However, the chapter on elliptic curves is an exception to the book’s mathematic simplicity in that it involves a much broader and deeper mathematical background than the rest of the text, with significant elements of number theory and some discussion of group theory; unavoidably, this coverage is much less complete.

Havil wields these mostly limited tools with great power and efficacy, if not extraordinary elegance or grace. The proof of de Moivre’s formula (a step toward the normal curve), which states that

\[\frac{1}{2^n}\Big({n \atop n/2}\Big) \approx 2 \frac{21}{125}\Big(1-\frac{1}{n}\Big)^n \frac{1}{\sqrt{n-1}}\]

for even \(n\), involves four pages of rather uninspiring symbol manipulation.

There is only one elegant proof in the book and it just gets a quick reference. At the very end of the chapter on constant-width curves, Havil quotes a theorem of Arthur Mellish. This theorem states that the following four conditions on a curve are equivalent: (i) it has constant width, (ii) it has constant diameter, (iii) all of its normals are double, and (iv) the sum of the radii of curvature at opposite points is constant. Havil then notes that “If we embrace [Hermann] Minkowski’s addition of ovals, it is quite obvious; it is not difficult to show that the sum of a curve of constant width with the same curve rotated through 180° is a circle of radius that width. The result is immediate.”

To a happy-go-lucky American like myself, Havil comes across as a no-nonsense British maths instructor of the old school. He might be willing to spend a few minutes after class showing students how to use cubic splines to replicate a sketch that Picasso made of his dachshund “Lump,” or demonstrating how one can express any \(106 \times 17\) pixelated black-and-white text in terms of the three in-equalities \(0 \le x < 106\), \(N \le y < N +17\), and 

\[\frac{1}{2} < \text{mod} \Big(\lfloor \frac{y}{17}\rfloor 2^{-17 \lfloor x \rfloor - \text{mod}( \lfloor y \rfloor, 17)}, 2\Big)\]

for the proper choice of \(N\). But before indulging in such frivolities, one must work through the three-page proof that confirms that the Weierstrass function \(W(x)=\Sigma^\infty_{n=0}  a^n \cos(b^n nx)\) is nowhere differentiable.

In fairness, Havil’s choice of theorems—and methods with which to prove them—presumably reflects his historical interests instead of purely mathematical criteria. He likes to present theories as they actually developed and proofs as they were constructed at the time; of course, these are now often of more historical than mathematical interest. Thankfully, Havil uses current terminology and notation rather than the original notations.

Curves for the Mathematically Curious includes a lot of interesting history of which I was not aware. Most of it stems from the Greek/Hellenistic era and the period from Newton to 1900, though the chapter on elliptic curves also contains compelling content from medieval and 20th-century mathematics. All of this text represents substantial, careful research and analysis on Havil’s part. The material sticks closely to mathematics and its applications; it does not dilly-dally with issues of biography, culture, or more general history. The “romance” in the book’s subtitle presumably refers to the equation for the conventional heart shape—\(x^2+(3y/4- \sqrt{|x|})^2 =1\)—that Havil provides at the end of the book. The only other mention of tender passion is Cantor’s honeymoon in Interlaken, Switzerland in 1874; Cantor spent much of this time discussing mathematical issues with Dedekind, who was also vacationing there.

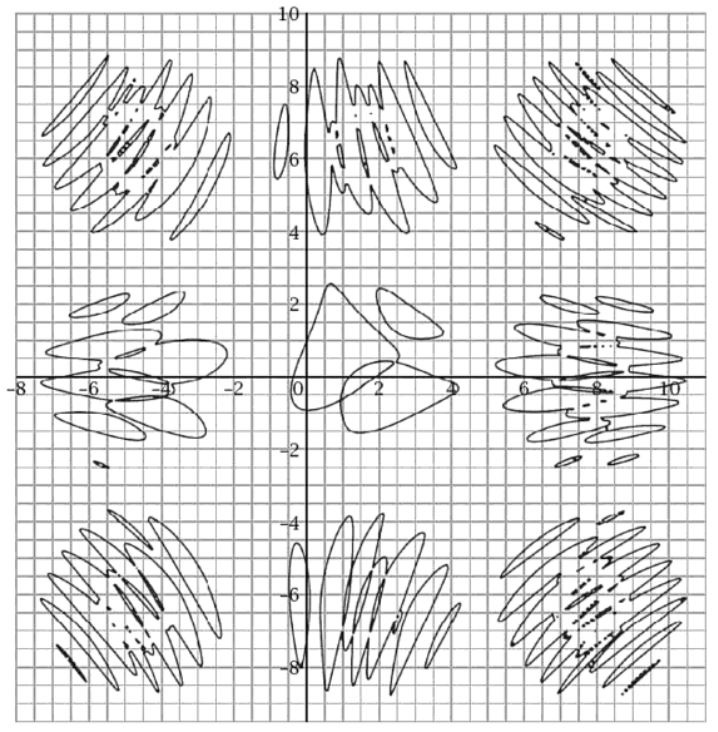
Havil raises one mystery that he neither discusses nor explains. At the very beginning of the book—before even the epigraph or table of contents—he includes the image in Figure 1: the graph of the equation \(\sin(\sin x+\cos y)=\) \(\cos(\sin xy+\cos x)\). This figure is certainly not mathematically elegant and probably not mathematically important, but it intrigues me nonetheless. Some of the plot’s characteristics—the square lattice arrangement of the blobs at intervals of \(2 \pi\), the imperfect symmetries, the blobs’ increasing complexity—are easily explainable in terms of the equation, but the precise forms are remarkable. Is there anything deeper here? What accounts for the lines of tiny closed curves (the dots are presumably all tiny closed curves) that are strung out like pearls inside the larger blobs? Do the blobs have a limiting behavior as one goes toward infinity in different directions? Is the image topologically correct, or has the plotting software introduced artifacts and flaws? Is this just a random pattern that Havil found while experimenting with plotting software, or does it have some more profound significance? Inquiring minds want to know.

All in all, readers who are interested in planar geometry and its history and are eager to satisfy their curiosity will find much to enjoy and learn in Curves for the Mathematically Curious.