The Brain Is a Dynamical System

In the human brain, \(\mathcal O(10^{11})\) neurons communicate mostly via electric impulses. Researchers often model the cerebral cortex as a coupled dynamical system: a large network with nodes that comprise smaller subsystems representing the dynamics of individual neurons. Of course, neuroscience is much more than such a network. Neuronal dynamics are driven by complicated biochemical processes on the molecular and intracellular levels, and outputs of cortical interactions affect cognition and behavior. But dynamical interactions of neurons play an integral role in brain function, and mathematics—particularly dynamical systems—can shed light on biologically meaningful models of these interactions.

Here I focus on primate vision [4]. The macaque monkey’s visual cortex is very similar to that of humans. This brain region is rich in data because experimentalists can access it easily, and its close proximity to sensory input enables researchers to correlate cortical responses directly to visual stimuli. These features make primate vision an ideal starting point for a biology-based quantitative theory. The visual cortex serves as a window into the rest of the cerebral cortex; it also offers a glimpse into the world of large and complex dynamical systems.

A Dynamical Model of LGN \(\rightarrow\) V1

Let us focus on a small piece of the action that occurs between the retina and the input layer of the primary visual cortex (V1). Between the retina and V1 lies a single structure called the lateral geniculate nucleus (LGN) (see Figure 1). LGN cells, which do not interact among themselves, relay signals from the retina to V1. There is a natural correspondence called the retinotopic map between a monkey’s retina or LGN and its visual field. Via this correspondence, an LGN cell at location \(x_0\) responds roughly linearly to visual input functions of the form

\[I_{\pm}(t) = \left[I_B \pm C \int_0^\infty \int_{-\infty}^\infty K(s)A(x_0-x) L(x, t-s) dx ds \right]^+ .\tag1\]

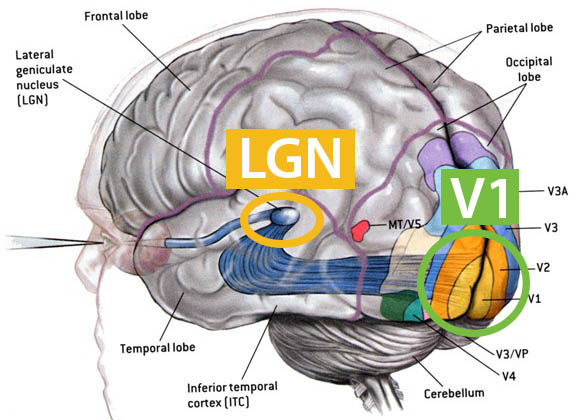
Here, \(L(x,t)\) measures light intensity at time \(t\) and location \(x\). The spatial kernel \(A(x)\) is a Gaussian-like function that describes the receptive field (RF) of the cell, \(K(s)\) is the temporal kernel, and \(I_B\) and \(C\) are constants. The RF of each LGN cell covers only a fraction of a degree; together, these small RFs tile the visual field. The temporal kernel \(K(s)\) takes the shape of a sine function, so convolving with it is akin to taking a time derivative in the luminance of the cell’s RF; i.e., LGN cells detect changes in luminance. The \(\pm\) in \((1)\) describes two kinds of LGN cells: ON cells that spike when their RF changes from dark to light, and OFF cells that do the opposite.

V1 is a much larger and more complicated network of excitatory (E) and inhibitory (I) neurons, the dynamics of which are described by the leaky integrate-and-fire equation: 

\[\frac{dv}{dt} = -\frac{1}{\tau} v - g_E(t)(v-V^E) - g_I(t)(v-V^I) .\tag2\] 

Here, \(v\) is the membrane potential of an E or I neuron. In normalized units, when \(v\) reaches 1, the neuron fires a spike and \(v\) resets to 0. The right side of \((2)\) describes the forces that act on \(v\): the first item is a leak term and the second and third terms are the E and I currents that run into the neuron. The E current is raised when the neuron receives a spike from either an LGN cell or another E cell; the I current, which has the opposite sign, is elevated in magnitude when the neuron receives an I spike. Each neuron has hundreds of presynaptic E and I cells, the spikes of which produce fluctuating current inputs that cause the dynamics of \(v\) to resemble a random walk with an upward drift. The postsynaptic neuron fires when \(v\) reaches 1, setting off similar changes in other neurons. More details are available in [1]. 

Detecting Edges and Tracking Moving Targets

We will now focus on two of the most basic visual capabilities in primates: orientation selectivity (OS) and direction selectivity (DS). OS refers to the fact that each V1 neuron has a preferred orientation. When a vertical-preferring neuron detects a vertical edge in its RF, it is excited and fires vigorously; the further the edge is from the neuron’s preferred orientation, the weaker the response. Since the RFs of neurons that prefer the full range of orientations cover each spatial location, V1’s spiking activity allows the brain to deduce the contours of objects.

Neurons also respond more vigorously to motion in specific directions. This capability, called DS, is implicated in pursuit eye movements. Even though the human visual field covers a wide angle, visual acuity is excellent in only a small region of two to three degrees at the center. To track a moving object, the brain must direct the eyes to the target; DS is crucial in this computation.

V1 neurons exhibit both OS and DS, yet LGN cells, which provide the sole source of feedforward input to V1, curiously possess neither capability. The remainder of this article will focus on the origins of OS and DS, which are of fundamental importance in theoretical neuroscience.

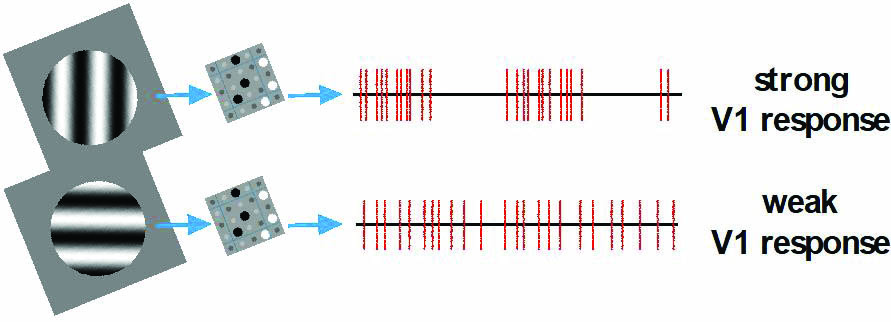
The wiring between the LGN and V1 is key to OS. David H. Hubel and Torsten N. Wiesel, who won the 1981 Nobel Prize in Physiology or Medicine for early experimental work that greatly advanced the field of visual neuroscience, hypothesized that each V1 cell is connected to two or three parallel rows of ON and OFF LGN cells [5]. Figure 2 illustrates OS in action. Here we assume that the three ON and three OFF LGN cells are afferent to a V1 cell. Recall that an ON cell is excited when the part of a drifting grating that passes over its RF changes from dark to light, while the opposite is true for OFF cells. When the grating and LGN align (as in the upper portion of Figure 2), all six LGN cells are simultaneously excited for half of the cycle and quiet the other half; this elicits a strong response from the V1 cell to which the LGN cells project. On the other hand, an orthogonal grating (as in the lower portion of Figure 2) excites half of the LGN cells at any given time, producing more evenly spaced LGN spikes that elicit a weaker response from V1. Notice that V1 response is driven by LGN spiking patterns, not their firing rates; the firing rates of LGN cells—which have no OS—are independent of grating orientation. Mathematically, spikes that arrive in rapid succession leave less time for the leak term in \((2)\) to act and can thus more effectively drive \(v\) across the threshold.

Mechanistic origins of DS in the macaque V1 eluded the neuroscience community for more than half a century. My collaborators and I recently proposed a biologically plausible explanation, an idealized version of which can be made rigorous [2, 3]. In addition to the usual analytical thinking, the challenge here also involved learning to distill relevant facts from anatomical and physiological data and to operate in the world of biology, where complexity is high and information is incomplete. Our findings are supported by simulations that use LGN\(\to\)V1 models of the kind described here and are in quantitative agreement with experimental data.

Though individual LGN cells do not have DS, we found that the summed response of LGN cells that are afferent to a V1 cell can have DS. For simplicity, consider one ON and one OFF cell (see Figure 3b). A sinusoidal signal produces a phase difference \(\delta\phi\) between the responses of the two cells because of their spatial displacement. When \(\delta \phi\) is small and the responses are in-phase, they amplify each other; when they are anti-phase, they cancel. The question is hence as follows: Why is \(\delta \phi\) different for signals from the left versus the right? Which biological properties are responsible for breaking this left-right symmetry?

We traced the answer to differences in the temporal kernels of ON and OFF cells (\(K_{\rm ON}\) and \(K_{\rm OFF}\), respectively). Experiments show that \(K_{\rm ON}\) is delayed and takes the form \(K_{\rm ON} = K_{\rm OFF} +\) a positive function (see Figure 3a). Figure 3b demonstrates the way in which a delay breaks left-right symmetry. Delays, however, are only effective for signals with relatively high temporal frequencies (TF). At lower TFs, directional bias can be explained heuristically: convolving a sine function with \(K_{\rm OFF}\) is like taking its derivative (which gives cosine), whereas convolving with a positive function is a form of averaging (producing another sine function). The addition of a sine function to a cosine shifts its phase.

Working at the interface of mathematics and neuroscience has convinced me that a partnership between the two subjects can be fruitful; I hope to have conveyed a sense of that potential in this short article. 

References

[1] Chariker, L., Shapley, R., & Young, L.-S. (2016). Orientation selectivity from very sparse LGN inputs in a comprehensive model of macaque V1 cortex. J. Neurosci., 36(49), 12368-12384.
[2] Chariker, L., Shapley, R., Hawken, M., & Young, L.-S. (2021). A theory of direction selectivity for macaque primary visual cortex. Proc. Natl. Acad. Sci., 118(32), e2105062118.
[3] Chariker, L., Shapley, R., Hawken, M., & Young, L.-S. (2022). A computational model of direction selectivity in macaque V1 cortex based on dynamic differences between on and off pathways. J. Neurosci., 42(16), 3365-3380. 
[4] Hubel, D.H. (1995). Eye, brain, and vision. In Scientific American Library. New York, NY: W.H. Freeman.
[5] Hubel, D.H., & Wiesel, T.N. (1962). Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J. Physiol., 160(1), 106-154.