The Loopy Fluid Dynamics of Bird Lungs

If asked why birds are such efficient aerodynamic machines, one may initially point to their streamlined bodies and finely contoured wings that seem tailored to manipulate the wind. But the aerodynamics behind birds’ mastery of flight is as much about the intricate structures and airflows inside as well as outside. Investigations into the nonlinear dynamics of flow networks with unusual topologies are breathing fresh air into a century-old mystery about bird lungs [7].

Biologists have long appreciated birds’ ability to breathe highly efficiently — a trait that is presumably connected with the extreme energetic demands of flight [5]. A classic experiment illustrates this point by stark comparison: in an enclosed chamber where oxygen has been depleted to such a level that a mouse is comatose and moribund, a similarly-sized sparrow playfully flitters about [10]. These remarkable respiratory abilities allow birds to migrate across oceans and continents and fly in thin air at elevations as high as Mount Everest [9]. It is thus with good reason that anatomists have carefully mapped out the structure of avian lungs and physiologists have charted the airflow patterns and currents [2].

The airflow in the lungs of most animals (including humans) oscillates with inhalation and exhalation. However, one-way or directed flows persist throughout the bird respiration cycle due to a unique topology that—unlike our own branched bronchial network—contains looped airways (see Figure 1a). The one-way flows arise as circulation around these loops, meaning that the time average of the fluid flux over a breathing cycle has a nonzero value. Bird lungs therefore exhibit a form of alternating current (AC) to direct current (DC) rectification, wherein the oscillatory AC airflow that is associated with inhalation and exhalation is converted to a directed DC flow around the loops. While researchers are still parsing through the details [6], it seems that this one-way flow of air allows for efficient gas exchange with the blood, which itself flows directionally within the circulatory system because of the one-way action of heart valves.

Lung valves, however, seem to be nothing but science fiction. In the 100 years since scientists first documented the phenomenon of one-way airflow, exhaustive searches for valvular structures by anatomists have come up empty [4]. Consequently, researchers have proposed many hypotheses that appeal to various structural features in the lung that may appropriately guide the flows, even without the opening and closing movements of conventional valves [1]. However, because anatomical details differ across species yet one-way flows are pervasive, we felt that a more general mechanism lurks in the fluid dynamics of loopy networks.

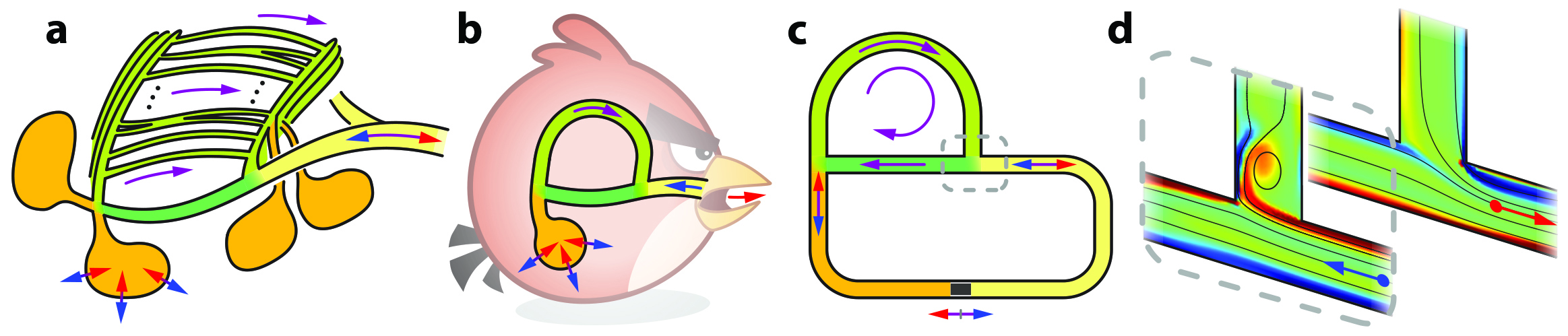
Rather than use a detailed model of a bird lung that captures all anatomical complexities, our recent study considers a “spherical bird” approximation that isolates a single loop in the network (see Figure 1b). We then transformed the system into the closed circuit in Figure 1c — an experimental and computational convenience for the study of internal flows. The network contains a fluid that is driven through the action of an oscillating piston, which plays the role of inhalation and exhalation in bird lungs. This system allows us to assess the way in which network geometry affects flow rectification. Specifically, our study aims to isolate the effects of the two loops that are connected by junctions. It initially seemed impossible for the loopy network to generate a DC flow. After all, if the network represents the flow of electrical current in a circuit that is modeled by a linear system of ordinary differential equations, one could readily conclude that no DC component exists. But flows in bird lungs are sufficiently fast to involve nonlinear fluid dynamical effects whose consequences in terms of flow patterns are still unknown.

Experiments that were conducted in the Applied Mathematics Laboratory at New York University’s Courant Institute of Mathematical Sciences involved a simplified model lung that was made of tubing filled with water. While the water near the piston simply sloshed back and forth, a DC flow spontaneously emerged in the upper loop — as long as the driving amplitude was sufficiently large. This directional flow represents the movement of fresh air in bird lungs that continuously ventilates oxygen-absorbing tissues.

While these experiments demonstrated that our simplified model generates directed flows, the fluid dynamical mechanism remained unclear. To dig deeper, we conducted numerical simulations of the two-dimensional incompressible Navier-Stokes equations with no-slip boundary conditions on the piston and the walls of the domain (see Figure 1c). The equations are

\[\rho\bigg(\frac{\partial\boldsymbol{u}}{\partial t}+\boldsymbol{u} \cdot \triangledown\boldsymbol{u}\bigg)=-\triangledown p+ \mu\Delta\boldsymbol{u},\] \[\triangledown \cdot \boldsymbol{u}=0.\]

Here, \(\boldsymbol{u}(\boldsymbol{x},t)\) and \(p(\boldsymbol{x},t)\) are the fluid velocity and pressure respectively, and \(\rho\) and \(\mu\) are the fluid density and dynamic viscosity. The left side of the first equation represents the fluid inertia and the two terms on the right side respectively account for pressure and viscous forces. We conducted the simulations using the finite element method and employed an Arbitrary Lagrangian-Eulerian formulation to treat the neighborhood of the moving piston.

These simulations allowed us to visualize the flow fields, which revealed a subtle interplay between inertial and viscous effects at the T-shaped junctions. Figure 1d highlights the key events. At peak velocity during inhalation (the first image in Figure 1d), fluid is injected from the right via the blue arrow and predominantly moves straight past the junction, with minimal turning up the side branch. This movement matches the intuition that the flow’s inertia causes it to maintain a straight course. Viscosity compels the flow to separate from the corner, resulting in a vortex that is shed and then “plugs” the side branch. At peak velocity during exhalation (the second image in Figure 1d), fluid exits the junction at the red arrow and draws more equally from the two branches because the vorticity that is produced at the corner “hugs” the wall instead of detaching to form a plug. Integrating in time over the course of a cycle, the indicated junction thus has a net flux that corresponds to circulation in the clockwise sense around the network’s upper loop.

What permits this rectification/pumping to occur without conventional valves? One key ingredient is that the fluid and operating conditions must allow both inertial and viscous effects to participate. Rectified flows of the type that we see here are impossible in viscous-dominated conditions where inertia is neglected; the governing Stokes equation is reversible and the so-called scallop theorem [8] ensures that flows induced in one stroke are retraced reversely in the return stroke. Kelvin’s circulation theorem means that rectification is also precluded in the other extreme of inviscid and irrotational flow (potential flow) [3]. In the parlance of fluid dynamics, such valveless rectification fails at the extremes of the Reynolds number, \(\rm{Re}=0\) and \(\rm{Re}= \infty\). Fortunately, there is a lot of room in between where the mechanism is operable!

Just as important are the junctions’ geometrical anisotropy and their connectivity to form the loops around which circulation develops. The junctions have distinct side and straight branches that tend to bias incoming flows. We do not believe that the T-shape in our study is critical, but some degree of anisotropy is important. The junctions must also be “wired” in a way that exploits the tendency of inertial flows to go straight. In our model, the straight branch of each junction feeds into the side branch of the other to form a loop that is then fed by both straight segments. One-way flows occur as long as we maintain this property, which we confirmed in additional experiments on networks with various geometries.

Our study focuses specifically on network topology and the nonlinear flows at junctions, but researchers have much more to do and understand. While there is beauty and power in the investigation of idealized systems, one cannot help but wonder about the roles of the many other lung complexities. This line of reasoning inspires mathematical questions about the optimization of junction shape, network structure, and kinematic forcing to enhance directed flows. Like all good mysteries, the unexpectedly fascinating aerodynamics of bird respiration endures. Our study has uncovered some clues but raises as many questions as answers.

References

[1] Banzett, R.B., Nations, C.S., Wang, N., Fredberg, J.J., & Butler, J.P. (1991). Pressure profiles show features essential to aerodynamic valving in geese. Respir. Physiol., 84(3), 295-309.
[2] Bretz, W.L., & Schmidt-Nielsen, K. (1971). Bird respiration: Flow patterns in the duck lung. J. Exp. Biol., 54(1), 103-118.
[3] Childress, S. (2009). An introduction to theoretical fluid mechanics. New York, NY/Providence, RI: Courant Institute of Mathematical Sciences and the American Mathematical Society.
[4] Duncker, H.-R. (1974). Structure of the avian respiratory tract. Respir. Physiol., 22(1-2), 1-19.
[5] Maina, J.N. (2000). What it takes to fly: The structural and functional respiratory refinements in birds and bats. J. Exp. Biol., 203(20), 3045-3064.
[6] Maina, J.N. (2017). Pivotal debates and controversies on the structure and function of the avian respiratory system: Setting the record straight. Biol. Rev. Camb. Philos. Soc., 92(3), 1475-1504. 
[7] Nguyen, Q.M., Oza, A.U., Abouezzi, J., Sun, G., Childress, S., Frederick, C., & Ristroph, L. (2021). Flow rectification in loopy network models of bird lungs. Phys. Rev. Lett., 126(11), 114501.
[8] Purcell, E.M. (1977). Life at low Reynolds number. Am. J. Phys., 45(1), 3-11. 
[9] Scott, G.R. (2011). Elevated performance: The unique physiology of birds that fly at high altitudes. J. Exp. Biol., 214(15), 2455-2462. 
[10] Tucker, V.A. (1968). Respiratory physiology of house sparrows in relation to high-altitude flight. J. Exp. Biol., 48(1), 55-66.