The Mechanics of the Powerball

The Powerball is a gyroscopic handheld wrist exerciser that was patented in 1973 by Archie L. Mishler. It is a gyroscope mounted inside of a plastic ball the size of an orange, with an opening that allows the user to give the gyro an initial spin. Surprisingly, by precessing the ball, one can cause the gyro to gain spin — and a remarkably fast one, capable of exceeding 250 revolutions per second. The resulting gyroscopic effect is so strong that a significant effort is required to precess the ball — hence the exercise value of the device.

How is one’s muscular effort converted into the gyro’s spin? In this article, I describe the idea behind Mishler’s admirable invention.

Construction of the Device

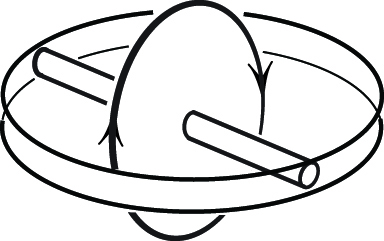
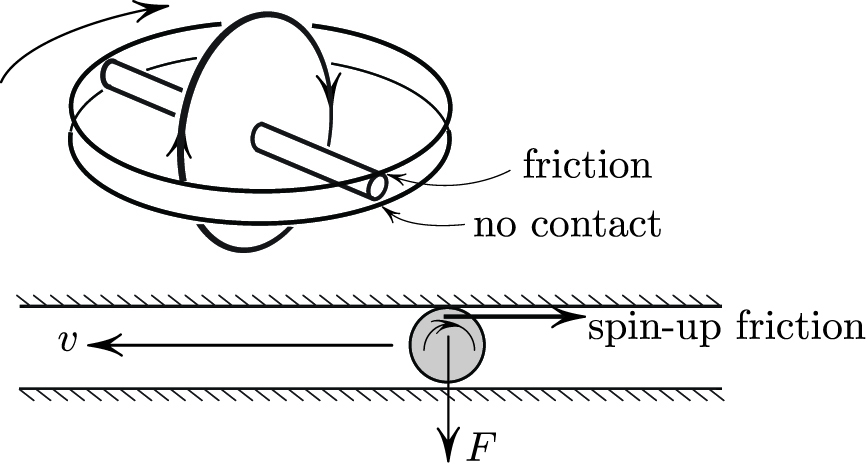
The ends of the gyro’s axle extend into an equatorial groove on the sphere’s inside surface,¹ which constrains the axle to lie in the ball’s equatorial plane (see Figure 1). Importantly, the axle is fused with the gyro; there are no bearings. When the gyro spins, so does the axle, rubbing against the wall of the groove that it touches. The axle is a tiny bit narrower than the groove, so it can only have contact with one wall.

The Spin-up Mechanism

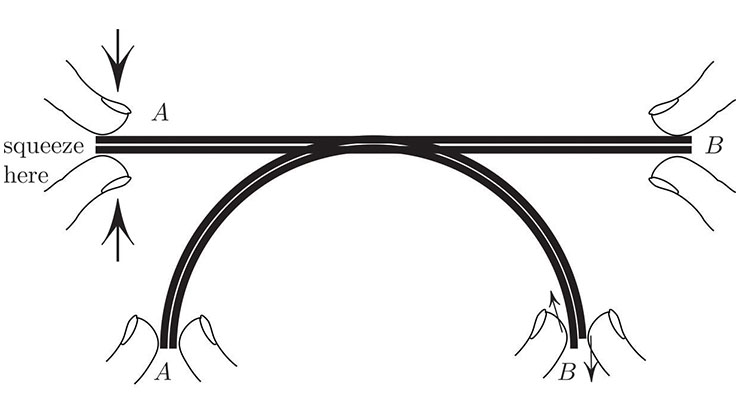
To understand how the Powerball works, let us recall the gyroscope’s key property (see Figure 2). The ends of a spinning gyro’s axle respond to the steady forces \(F\) that are applied by moving in a perpendicular direction.²

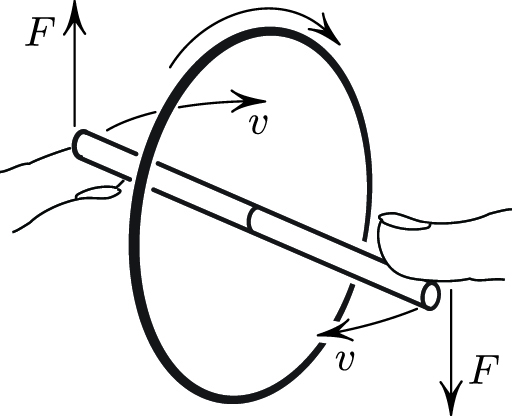
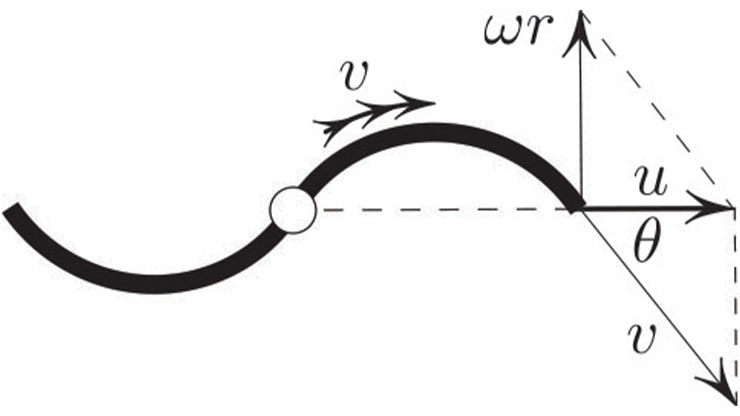
With the gyro having been given its initial spin, we tilt the ball to apply force \(F\) to the axle (see Figure 3). As in Figure 2, the axle responds by moving as shown. If the speed \(v> \omega r\) (where \(\omega\) is the spin angular velocity and \(r\) is the axle’s radius), then friction facilitates the gyro’s rotation. This explains the workings of the Powerball.

Is it luck, or is there a deeper reason that the axle in Figure 3 responds by moving to the left? Had it moved right, the friction would have acted against the spin and we would be holding a dud! In that case, I believe that we could still salvage the idea by adding a differential mechanism (though doing so would probably make the idea impractical).

In conclusion, here are two gyroscope-related remarks.

Gyro as a Charged Particle on the Sphere

A gyroscope with perfect bearings is mathematically equivalent to an electrically charged point mass that is constrained to the sphere and subject to a magnetic field that is perpendicular to the sphere. The charge is proportional to the gyro’s axial angular momentum. The Lagrange top (an axisymmetric top) is also equivalent to the particle on the sphere with a magnetic field, but with additional gravitational force [1]. This observation makes the treatment of the Lagrange top much more transparent than in standard textbooks on the subject.

Sperry’s Gyrocompass

The behavior of the gyro in Figure 2 amounts to Newton’s second law for rotational motion: applied torque equals the rate of change of angular momentum. Loosely speaking, the gyroscope tries to align its axis with the axis of applied torque. Sperry’s gyrocompass (still used in ships) works on this principle: a spinning gyro floating in a dish with its axis in a horizontal position orients itself in a north-south direction due to the Earth’s rotation. The gyroscope tries to align itself with the Earth’s rotational axis while keeping its own axis horizontal.

¹ Precise details of construction—which I discovered by breaking apart my toy once it stopped working—are not important for the purpose of this discussion.

² This reaction occurs because changing the orientation of the axle causes paths of the wheel’s particles of the sphere (to which they are confined) to acquire nonzero geodesic curvature. The resulting centrifugal force creates gyroscopic torque [2].

The figures in this article were provided by the author.

References
[1] Cox, G., & Levi, M. (2018). Gaussian curvature and gyroscopes. Commun. Pure Appl. Math., 71(5), 938-952.
[2] Levi, M. (2014). Classical mechanics with calculus of variations and optimal control: An intuitive introduction. Providence, RI: American Mathematical Society.