Volume 49 Issue 09 November 2016
Research

The Thin Lens Formula and Springs

By

The thin lens formula relates the locations of an object and the image created by a thin lens (see Figure 1):

\[\frac{1}{d_1}+ \frac{1}{d_2}= \frac{1}{f}. \tag1\]

The meanings of \(d_1\), \(d_2\), and \(f\) are explained in the figure. The following mechanical interpretation of this formula hopefully makes the formula more transparent (apologies for the pun).

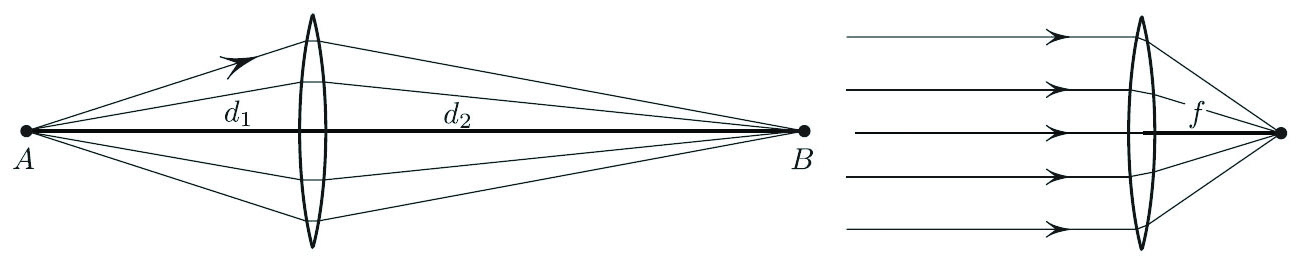
<strong>Figure 1.</strong> Illustration of the lens formula. The lens is meant to be of near-zero thickness (this would require, for a fixed <i>f</i>, that the index of refraction of the glass be near-infinite). Image credit: Mark Levi.
Figure 1. Illustration of the lens formula. The lens is meant to be of near-zero thickness (this would require, for a fixed f, that the index of refraction of the glass be near-infinite). Image credit: Mark Levi.

If the rays emanating at \(A\) focus at \(B\), as in Figure 1, then all these rays have the same optical length, i.e., they all take the same time to travel. According to Pierre de Fermat, each ray takes the path of least time; if the minimizers of a functional form a continuous family, as our rays do, then the functional is constant on this family. Now the travel time as the function of the deflection \(s\) in Figure 2 is given by

\[T(s) = L_1+L_2+ c+\frac{1}{2} k s ^2, \tag2 \]

where \(c+ \frac{1}{2} k s ^2\) is the time it takes the light to travel through the lens; \(k < 0\) for the magnifying lens, since the thickness decreases with \(s\). To summarize, the rays focus at \(B\) if \(T(s)= \textrm{const.}\)

&lt;strong&gt;Figure 2.&lt;/strong&gt; The mechanical analog of the optical system in Figure 1. The point &lt;i&gt;S&lt;/i&gt; is constrained to the vertical line through &lt;i&gt;O&lt;/i&gt;. Image credit: Mark Levi.
Figure 2. The mechanical analog of the optical system in Figure 1. The point S is constrained to the vertical line through O. Image credit: Mark Levi.

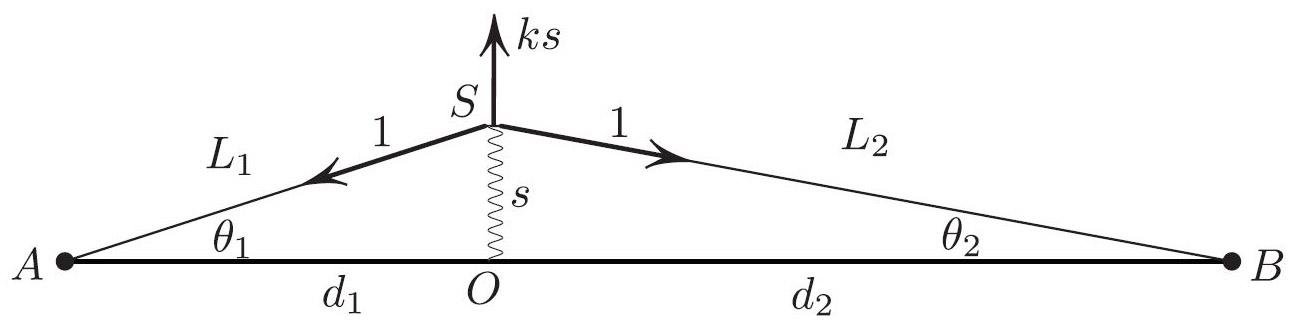
To explain the thin lens formula \((1)\), let us interpret \(T(s)\) as the potential energy of a mechanical system sketched in Figure 2. \(AS\) and \(SB\) are constant tension springs of \(\textrm{tension}=1\), and \(OS\)  is a Hookean spring with Hooke’s constant \(k\) (for \(k=0\), the spring tries to expand with the force proportional to its length \(s\)). The potential energy of this system is precisely the time \((2)\). The focusing condition \(T(s)= \textrm{const.}\) thus also says that the potential energy of our system is constant, or equivalently, that our system is in equilibrium for any \(s\) or that the forces upon \(S\) (see Figure 2) cancel out:

\[\sin \theta_1+ \sin \theta_2+ks=0.\tag3\]

Substituting \(\sin\theta_i= s/d_i + o( s ^2 ), i=1,2\) into \((3)\) and dividing by \(s\) yields 

\[\frac{1}{d_1}+ \frac{1}{d_2}+k =0,\]

which reproduces the lens formula \((1)\), where \(f=- k\).

To summarize, the thin lens formula amounts to an equilibrium condition of a simple mechanical system. Both sides of the formula acquire a direct physical interpretation: \( f=-1/k \) is the negative reciprocal of Hooke’s constant, and

\[\frac{1}{d_1}+ \frac{1}{d_2}\]

is the Hooke’s constant of vertical displacement of the two combined springs \(AS\) and \(SB\).

About the Author

Mark Levi

Professor, Pennsylvania State University

Mark Levi (levi@math.psu.edu) is a professor of mathematics at the Pennsylvania State University.