Understanding Jupyter as a Valuable Student Resource for Computational Discovery

The following is a brief description from the authors of Computational Discovery on Jupyter, which was published by SIAM in 2023. The text uses Python, a popular programming language, to expose students to mathematical ideas outside of the standard curriculum. Multimedia materials, associated Jupyter Notebooks, and sample projects facilitate an active learning approach and encourage students to interact and play with the concepts.

Computational Discovery on Jupyter utilizes deliberately nonstandard and offbeat computational topics to motivate the notion of mathematical proof and inspire students to write small computer programs. Each of the seven chapters contains multiple “activities” that promote further exploration, and the appendix includes a complete report on every activity. With guidance from these examples, the book prompts students to ask their own questions.

The Target Audience

The text is meant for students who are just entering university. It contains almost no proofs because we concur with the dictum of Ed Barbeau—professor emeritus at the University of Toronto—that “there should be no proof without doubt” (in this case, doubt on the student’s part about the result). Similarly, during a conference at the Pennsylvania State University in 1994, the late physics professor Henry Abarbanel stated that “I have absolutely no interest in proving things that I know are true.” This attitude is widespread throughout the community.

Teachers generally wish to motivate their students to actually want to prove things, but they must overcome several obstacles in order to do so. We wrote this book—which we originally conceptualized as an online educational resource, rather than a full publication—to help surmount some of these challenges. Because many high school curriculums have eliminated proofs from their lesson plans, the first hurdle is that incoming college students have much less experience with proofs than in the past.

Therefore, we decided to sneak up on the idea of proof from a different angle. We also want students to discover things on their own, so we encourage active learning with rich mathematical topics (like continued fractions) that leave room for experimentation. Writing small programs that perform unusual computations quickly leads to “bugs,” as such programs often do not behave as expected. This, we find, is a natural place to plant the seeds of doubt.

Students are typically eager to learn to code, and use of the popular language Python (as well as Maple) inside the Jupyter Notebook environment allows for some economy of effort on their part. The skills within Computational Discovery on Jupyter are easily transferable to other topics, and the exploration of simple mathematical concepts is perhaps the most straightforward path to programming that we are likely to find.

Purpose and Intent

By highlighting offbeat topics with motivating applications and appealing images, we hope to attract a wide pool of students who are potentially interested in mathematical careers. For instance, students really seem to delight in the inclusion of Bohemian matrices [1] and appreciate the project-based nature of the work. While instructors probably could use this book for an exam-based course, we have not done so.

Given its many possibilities, this book is not going to simplify your life as an instructor. It will, however, make coursework more fun for both you and your students.

Open Problems

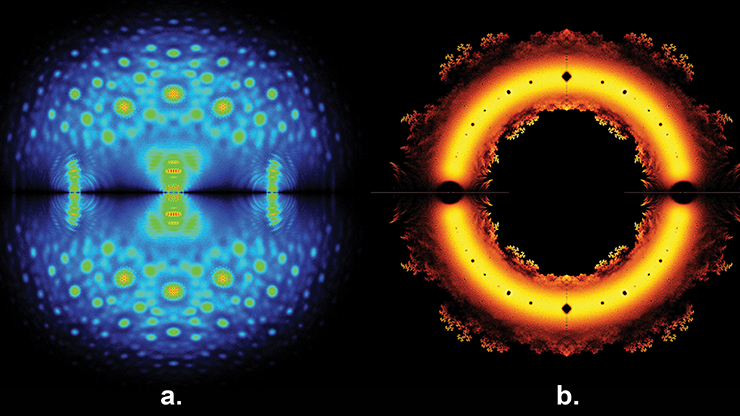
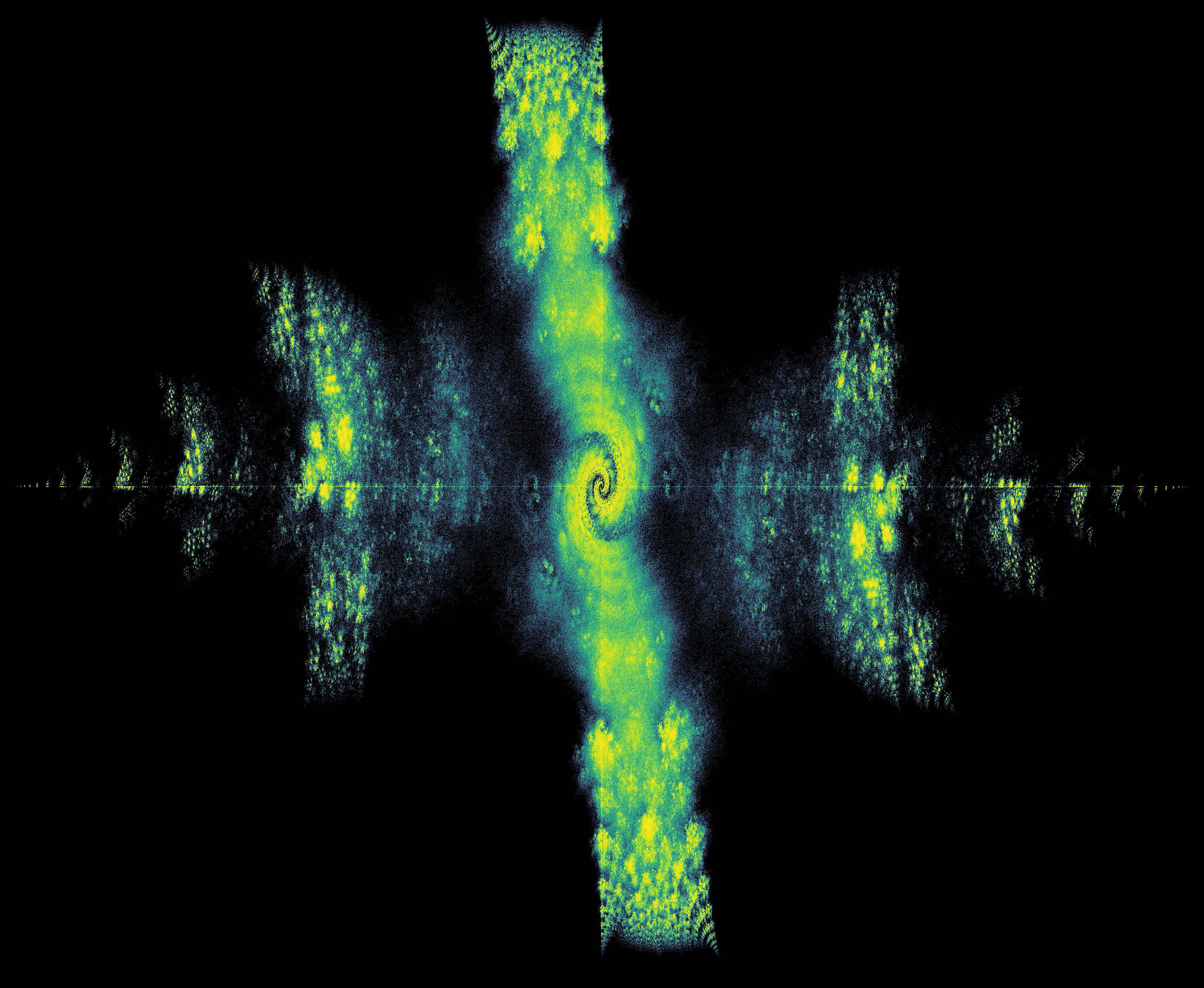
Another goal of the text is to introduce students to open problems, which appear in every chapter. To be sure, the majority of them are not “serious” problems — they are mostly just problems for which we do not have answers. For instance, Figure 1 contains a visible spiral in the center even though the image depicts a plot of the density of all eigenvalues of a particular Bohemian family of matrices. Each matrix is \(14\times 14\), skew-symmetric, and tridiagonal; they draw their nonzero entries from the finite population \(2\), \(5i\), and \(2+i\), where \(i^2=-1\). Why should the eigenvalues spiral? We simply do not know.

In addition to witnessing their teachers’ occasional bafflement with existing images, students like to generate their own images that also sometimes baffle us. In fact, some of the figures on our Bohemian matrices website were created by students and gave rise to questions (e.g., about circulant matrices) that still remain unanswered.

We had a lot of fun writing Computational Discovery on Jupyter and enjoy teaching with this material. We believe that other instructors can come up with creative new ways to use the text, and we wish you joy and success in your teaching endeavors.

Enjoy this passage? Visit the SIAM Bookstore to learn more about Computational Discovery on Jupyter and browse other SIAM titles.

References
[1] Higham, N. (2018, December 3). Rhapsodizing about Bohemian matrices. SIAM News, 51(10), p. 2.