Understanding Uncertainty in Glacier Models — Before the Ice Melts

Rising ocean levels pose a major threat to coastal cities and island nations around the world [1, 4]. As average global temperatures continue to increase, melting glaciers and sea ice contribute significantly to this urgent problem. For this reason, researchers currently use a wide variety of mathematical and observational techniques to gauge the rate at which ice is melting, the locations at which melting is most severe, and the extent to which those factors affect sea level change.

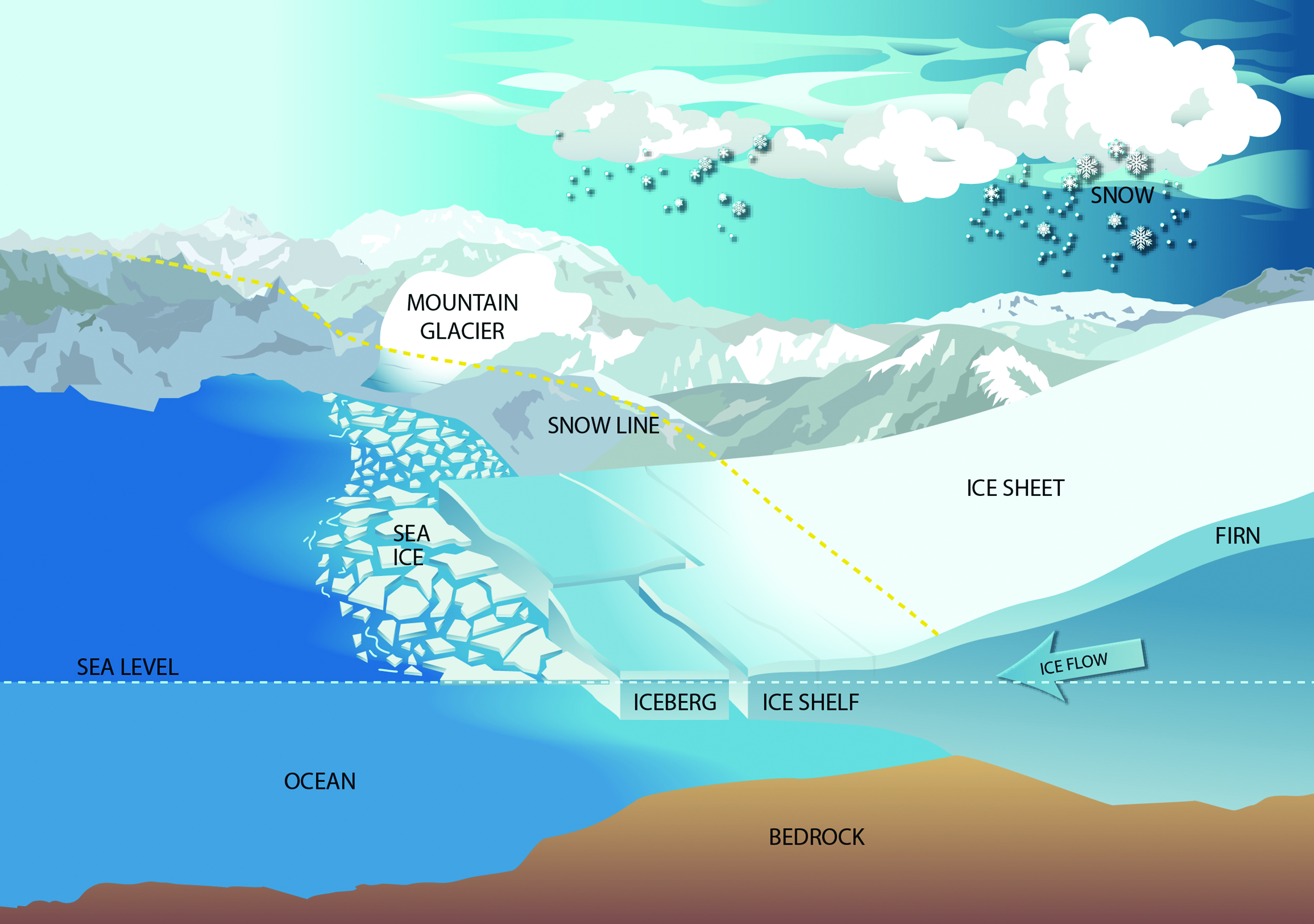
Unfortunately, the paucity and limited accessibility of important data hampers model development and subsequently complicates forecasting efforts. In turn, scientists must communicate the resulting uncertainty to policymakers and the general public. These connected challenges were the subject of a scientific session at the 2024 American Association for the Advancement of Science (AAAS) Annual Meeting, which took place in Denver, Colo., this February. The speakers discussed ongoing research in Antarctica, which houses much of the planet’s ice atop the continent itself, as well as on and in the surrounding ocean (see Figure 1).

“We can use our knowledge of these [ice] models to understand what we don’t know about them,” said Nicole-Jeanne Schlegel of the Geophysical Fluid Dynamics Laboratory at the National Oceanographic and Atmospheric Association (NOAA). By tweaking the parameters of existing physical models of glaciers, she and her colleagues can quantify the largest uncertainties. “[It’s] not just the sea level or the [ice distribution] map,” Schlegel continued, “but the uncertainty and the way in which models and data together can help each other.”

Meanwhile, statistician Won Chang of the University of Cincinnati approaches the problem from a data angle. “Once you create a model, you should now be able to fit that model to the data,” he said. “To fit the model to the data [when] many of the important parameters are unknown, you need to be able to adjust those parameters so that the model actually behaves similar to reality. For complicated models—like physical models of Antarctica—you really have to do complicated statistical analysis to actually get those uncertainties.”

In a system with multiple parameters that cannot be directly measured, scientists must apply advanced statistical techniques to determine the ranges of possible values that could return the same observational data. Chang seeks to develop user-friendly tools for this challenging, multidimensional problem to assist climate researchers who do not have advanced statistical training.

A Parametric Hydra

Antarctica’s ice comprises three basic forms: (i) Land ice, including glaciers; (ii) ice shelves, which extend from land but rest directly on the sea floor; and (iii) sea ice, which is attached to either land ice or ice shelves but floats on ocean water (see Figure 2). Sea ice is the most variable of those forms, particularly as climate change drives summer temperatures high enough to melt all of it — even at high latitudes.

Ice shelves are also under threat. In 1986, a 4,000-square-kilometer iceberg broke free of the Filchner Ice Shelf; it was too heavy to float away until 2023, when it finally drifted into the open ocean [5]. Scientists anticipate similar large-scale iceberg calving events—which represent the most dramatic type of Antarctic ice loss, if not the most directly concerning—in the future. In any case, melting ice can increase the volume of the ocean and contribute to higher water levels far from its Antarctic origins.

Schlegel noted that most data about ice coverage in Antarctica comes from the surface: melting atop ice sheets, glacier speeds, snowfall levels, and so forth. She also remarked that it is difficult to obtain reliable values for under-ice properties, such as the amount of liquid water beneath glaciers and the topography of the rock under ice. Ice that is several kilometers thick is heavy enough to compress the underlying rock, and a lack of data hinders the documentation of the way in which the surface rebounds as ice melts and shifts.

Meanwhile, ice cores allow researchers to track changes over the course of decades or even centuries; they provide some of the best evidence of humanity’s role in climate change but are less helpful for understanding ice dynamics on shorter time spans. “In the last 20 or 30 years, we’ve seen that ice can flow and change faster than we ever thought,” Schlegel said. “What’s going on under the ice, how the ice is flowing, how water might get from the surface to the base of the ice — these are the new parameterizations that we need to put in the models to know what will occur over the next decade.”

A common model for ice sheets is built upon the Stokes equations:

\[\triangledown \cdot \boldsymbol{\sigma} + \rho \mathbf{g} =\mathbf{0},\]

where \(\mathbf{g}\) is the gravitational vector and \(\rho\) is the ice density [2, 3]. The stress tensor \(\boldsymbol{\sigma}'=2\mu\dot{\boldsymbol{\varepsilon}}-p\mathbf{I}\) includes the pressure \(p\), the effective viscosity \(\mu\), and the time derivative of the strain tensor \(\dot{\boldsymbol{\varepsilon}}\) \((\)along with the identity tensor \(\mathbf{I}).\) The viscosity and strain are nonlinearly dependent on temperature, as well as on other physical parameters that are not necessarily easy to measure.

These parameters are not just uncertain; they also have overlapping influences on both the mathematics and the observable effects [6]. Understanding this overlap will help researchers design better models, quantify possibilities for decision-makers, and propose new experiments. “You can test the model to see what type of observations would help us be more certain about what’s going on,” Schlegel said. “Then you can go back to NOAA and NASA and say, ‘Hey, we need a satellite that can measure this [property] on this frequency.’”

From Finance to Climate

Better data is essential, but data alone cannot reveal what can or will happen in the coming years or decades. To make such predictions, climate scientists need models, interpretations of simulations, and quantifications of uncertainty.

Chang first applied statistics to financial models while working towards his master’s degree, but he later began to collaborate with climate researchers as part of his Ph.D. studies when he realized that the same advanced math is relevant to both topics. Drawing on models that were developed by climatologist David Pollard of the Pennsylvania State University, Chang’s AAAS presentation focused on four major unknown parameters: (i) The rate at which ice melts into the ocean, (ii) the rate of iceberg calving, (iii) the coefficient of friction between ice and bedrock, and (iv) the rate at which bedrock rebounds as the ice’s weight decreases.

“You’re trying to match the data and model outcome, but you don’t have one best value [for each parameter],” Chang said. He uses Bayesian methods to generate a multidimensional likelihood density function, for which the best parameter estimates give the maximum likelihood. Since glacier models are complicated and cannot be inverted analytically to produce parameter matches, likelihood fitting involves iteratively changing parameters within the model and running simulations until the density space is fully mapped out.

Of course, this method becomes increasingly unwieldy with more parameters. “One active research goal in the future is to actually create a method that can handle a higher-dimensional parameter space,” Chang said. This type of ambitious project would benefit researchers across a variety of fields.

Telling the Statistical Story

The mathematical problem is only the beginning for climate science, and Chang hopes that his work will appeal to researchers beyond the field of statistics. “This Bayesian inversion stuff is great,” he said. “But I need to perhaps change the methodology or some of the statistical tools to make it much easier for glaciologists to actually use.” He also noted that many current statistical methods are not always directly applicable to dynamical systems, such as glacier or atmospheric models. Chang feels that applied mathematicians and statisticians have much to learn from each other, and their collaborations could potentially yield powerful, reliable models that predict various scenarios about emissions and mitigation efforts.

Schlegel added that the communication of statistical uncertainty is a major challenge for climate researchers. Politicians, decision-makers, and the general public are typically not interested in ranges of possible sea level rise, much less Bayesian likelihoods; they want to know what will happen and how to respond. Meanwhile, climate change deniers seize upon statistical uncertainties—an inevitable consequence of science—to cast doubt on the entire enterprise.

Science happens at the intersection of theory, observation, and analysis. When attempting to forecast the future of Antarctic ice and its corresponding effect on sea level rise, understanding and limiting uncertainty at that intersection is the only way to effectively move forward.

References

[1] Cappucci, M. (2019, August 8). Sea level rise is combining with other factors to regularly flood Miami. The Washington Post. Retrieved from https://www.washingtonpost.com/weather/2019/08/08/analysis-sea-level-rise-is-combining-with-other-factors-regularly-flood-miami.
[2] Castleman, B.A., Schlegel, N.-J., Caron, L., Larour, E., & Khazendar, A. (2022). Derivation of bedrock topography measurement requirements for the reduction of uncertainty in ice-sheet model projections of Thwaites Glacier. Cryosphere, 16(3), 761-778.
[3] Larour, E., Seroussi, H., Morlighem, M., & Rignot, E. (2012). Continental scale, high order, high spatial resolution, ice sheet modeling using the Ice Sheet System Model (ISSM). J. Geophys. Res., 117(F1), F01022.
[4] Manzo, D., Zee, G., Uddin, S., & Jovanovic, D. (2021, November 3). Facing dire sea level rise threat, Maldives turns to climate change solutions to survive. ABC News. Retrieved from https://abcnews.go.com/International/facing-dire-sea-level-rise-threat-maldives-turns/story?id=80929487.
[5] Mathewson, S. (2023, November 29). Satellites watch world’s largest iceberg break away from Antarctica. Space.com. Retrieved from https://www.space.com/satellites-watch-worlds-largest-iceberg-move.
[6] Schlegel, N.-J., Seroussi, H., Schodlok, M.P., Larour, E.Y., Boening, C., Limonadi, D., … van den Broeke, M.R. (2018). Exploration of Antarctic Ice Sheet 100-year contribution to sea level rise and associated model uncertainties using the ISSM framework. Cryosphere, 12(11), 3511-3534.