Uniform-in-diffusivity Chaotic Mixing and the Batchelor Spectrum

Many observations of the statistical properties of fluids in physically relevant settings agree with the analytical theories of turbulence that stem from the engineering and physics communities; these theories combine various reasonable approximations with axioms that researchers derive from experimental observation. Although the theories successfully obtain accurate and useful approximations for physical observations, no mathematically rigorous justifications currently exist that start from the governing Navier-Stokes equations and systematically deduce these predictions — not even in extremely idealized situations, i.e., in a periodic box with stochastic white-in-time forcing. This goal of mathematical rigor is the ultimate verification that the governing equations are indeed sufficiently predictive of the true, observed behavior and accurately model the most relevant physics.

An important statistical problem in fluid mechanics concerns the long-time behavior of the density \(g_t\) of some scalar quantity that is passively advected by an incompressible fluid velocity \(u_t\) while also undergoing a small amount of molecular diffusion. Examples of this phenomenon are abundant in nature and include small fluctuations of temperature, pollutants, and salinity levels in the atmosphere or ocean, and even the presence of milk in one’s coffee or tea. The evolution of \(g_t\) is governed by the advection-diffusion equation

\[\partial_tg_t + u_t\cdot\nabla g_t - \kappa \Delta g_t = s_t,\tag1\] 

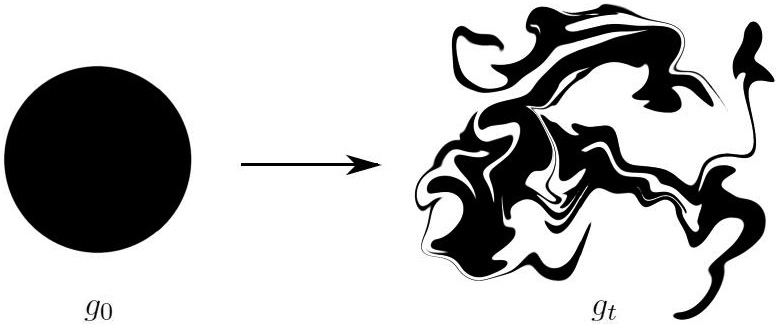
where \(\kappa>0\) is the diffusivity parameter and \(s_t\) is a source that continually replenishes \(g_t\). In many applications, stretching and folding within the fluid often causes the scalar to get “tangled up.” It eventually settles into a statistical steady state of “swiss roll” structures that have complex self-similar properties across a wide range of spatial scales (see Figure 1).

The statistics of \(g_t\) under generic fluid motion \(u_t\) is often referred to as passive scalar turbulence. We study one particularly simple regime within the wider range of possibilities: the Batchelor regime, where the molecular diffusivity \(\kappa\) is taken to be small relative to the fluid’s regularity. In particular, we fix the Reynolds number and study asymptotics as \(\kappa \to 0\).

George Batchelor took an important step towards understanding this regime in 1959 [2]. He predicted a \(|k|^{-1}\) power law—now known as Batchelor’s law—for the \(L^2\) power spectral density of \(g_t\) along frequencies \(k\) in the so-called viscous convective range. Length scales are sufficiently small such that the fluid motion is dominated by viscosity, but large enough so as not to be dissipated by molecular diffusion.

More precisely, consider an incompressible fluid in the periodic box \(\mathbb{T}^d\) where \(d = 2\) or \(3\), and let \(g_t\) be a solution to \((1)\). With \(\hat{g}_t(k), k \in \mathbb{Z}^d\) as the Fourier transform of \(g_t\), one can state Batchelor’s prediction as

\[|k|^{d-1} \mathbf{E}|\hat{g}(k)|^2 \sim |k|^{-1} \quad \text{for}\quad \ell_D^{-1} \leq |k| \leq \kappa^{-1/2},\]

where \(\ell_{D}\) denotes the fluid’s dissipative scale. Researchers have observed Batchelor’s prediction on the spectrum in a variety of settings, such as temperature and salinity variation in the upper ocean [8], laboratory experiments [7], and numerical studies [1]. These works imply that it has a robust and universal character in the class of spatially regular flows.

Despite the success of Batchelor’s prediction, no mathematical justification exists outside of highly restrictive settings or toy models. Here we report our recent mathematical results on passive scalar mixing and the first proof of Batchelor’s law when the velocity field evolves according to a class of physically-motivated random fluid models. An important example is the incompressible stochastic Navier-Stokes equations on \(\mathbb{T}^2\):

\[\partial_t u_t + u_t\cdot\nabla u_t + \nabla p_t - \nu \Delta u_t = \xi_t, \\ \textrm{div} u_t =0.\tag2\]

Our work assumes that the stochastic forcing \(\xi_t\) is a non-degenerate, white-in-time, sufficiently regular-in-space Gaussian forcing. One can consider the viscosity parameter \(\nu > 0\) to be the inverse Reynolds number.

In this setting, we show a cumulative version of Batchelor’s prediction on the power spectrum for fixed Reynolds number flows. In the subsequent text, \(\Pi_{\leq N}\) denotes the projection onto frequencies that are less than \(N\).

Theorem 0.1

Let the source \(s_t\) in \((1)\) be a white-in-time Gaussian process that is supported at large scales, and let \((2)\) give \(u_t\) with non-degenerate, white-in-time, sufficiently regular-in-space Gaussian forcing [5]. Let \(\nu > 0\) be fixed. There then exists a unique stationary probability measure \(\mu^\kappa\) for \((u_t,g_t)\) and \(C_0, N_0\geq 1\) that are independent of \(\kappa\) but dependent on \(\nu\), such that for all \(\kappa \in (0,1)\), 

\[\frac{1}{C_0}\log N \leq \mathbf{E}_{\mu^\kappa} \|\Pi_{\leq N}g\|^{2}_{L^2}  \leq C_0\log N \quad \text{for}\quad N_0 \leq |k|\leq \kappa^{-1/2}.\]

The mixing properties of the velocity field \(u_t\) play a crucial role in obtaining Batchelor’s law. Specifically, if the initial blob of scalar \(g_0\) has a large characteristic length in the absence of a scalar source \((s_t=0)\) and molecular diffusivity \((\kappa = 0)\), \(u_t\) will often cause the blob to become filamented and quickly generate smaller scales as it disperses evenly throughout the fluid. Figure 2 depicts an illustration of this process, which is commonly called mixing.

To make the process more precise, consider the scalar initial value problem

\[\partial_t g_t  + u_t \cdot \nabla g_t = \kappa \Delta g_t.\tag3\]

Researchers often quantify the mixing of scalar \(g_t\) with a negative Sobolev norm, particularly the \(H^{-1}\) norm \(\|g_t\|_{H^{-1}} := \|(-\Delta)^{-1/2}g_t\|_{L^2}\) that measures the average filamentation width (weighted by the total \(L^2\) scalar mass that is present in the fluid) [9].

Without molecular diffusivity \((\kappa = 0)\), one can easily show that \(\| g_t\|_{H^{-1}}\) can decay at most exponentially fast when \(u_t\) is Lipschitz-regular. In general, any solution \(g_t\) to \((3)\) is exponentially mixing if there exists \(\gamma>0\) and \(D\geq 1\), such that the following holds for all mean zero \(g_0\) in \(H^1\): 

\[\|g_t\|_{H^{-1}}\leq D e^{-\gamma t}\|g_0\|_{H^1}.\tag4\] 

The crucial ingredient to proving Theorem 0.1 is to show that solutions to \((2)\) are exponentially mixing with a rate \(\gamma\) that is uniform in diffusivity \(\kappa\). Several works collectively prove the following theorem [3, 4, 6].

Theorem 0.2

This theorem pertains to uniform-in-diffusivity, almost-sure exponential mixing [6]. Let \((u_t)\) solve \((2)\). For all \(\nu > 0\), a deterministic \(\gamma > 0\) exists such that a random (almost surely finite) constant \(D = D_\kappa(u,\omega)\) is present for all initial conditions \(u_0\), noise paths \(\omega\), and \(\kappa \in [0,1]\). This means that for every zero-mean \(g_0 \in H^1\), \((4)\) holds for all \(t > 0\). The random constant \(D\) has second moment finite uniformly in \(\kappa\): 

\[\mathbf{E} D^2 \leq C(u_0).\]

\(C(u_0)\) only depends on the initial velocity \(u_0\); in fact, it depends only on the \(L^2\) norm of \(u_0\) and its derivatives [6]. 

An important feature of this theorem is that \((4)\) holds almost surely, so that nearly every fixed noise path \(\omega\) gives an exponentially mixing velocity field \(u_t\) (which is deterministic after \(\omega\) is fixed). While \(D\) is random and depends on the velocity field’s initial condition, \(\gamma\) is deterministic and only depends on the structural parameters (e.g., the noise coloring, \(\nu\), etc.).

The proof of Theorem 0.2 uses a blend of mathematical ideas from random dynamical systems, spectral theory of Markov processes, and stochastic partial differential equations. Details and the theorem’s proof are available in [3, 4, 6], and the proof of Batchelor’s law (as in Theorem 0.1 from Theorem 0.2) is available in [5].

The proof of Batchelor’s power law for scalars that are advected by spatially regular incompressible velocity fields \((u_t)\)—such as \((2)\) on the periodic box \(\mathbb{T}^d\)—provides some insight into the validity of Batchelor’s law outside this strict, mathematically expedient setting. We now generally know when to expect the spectrum, even when a complete mathematical proof is not readily available.

Our results only scratch the surface of potential mathematically rigorous outcomes in this area. We believe that more sophisticated studies will prove our results for \((2)\) when subjected to more realistic stochastic forcing — at least when the forcing is \(k\)-times differentiable in time and smooth in space. Similarly, studies of fluid that is driven by the stochastic motion of solid boundaries rather than somewhat non-physical body forcing would yield substantial value. However, much mathematical work must still be done before more complicated statistical problems—like Navier-Stokes at a high Reynolds number with stochastic forcing—are tractable. Indeed, although the proofs of Theorems 0.1 and 0.2 require many mathematical ideas, they are certainly among the easiest of such statistical questions in fluid mechanics. Nevertheless, we hope that our advancements will help spur new activity and eventually lead to larger progressions in these directions.

References

[1] Antonia, R.A., & Orlandi, P. (2003). Effect of Schmidt number on small-scale passive scalar turbulence. Appl. Mech. Rev., 56(6), 615-632.
[2] Batchelor, G.K. (1959). Small-scale variation of convected quantities like temperature in turbulent fluid part 1: General discussion and the case of small conductivity. J. Fluid Mech., 5(1), 113-133.
[3] Bedrossian, J., Blumenthal, A., & Punshon-Smith, S. (2018). Lagrangian chaos and scalar advection in stochastic fluid mechanics. J. Euro. Math. Soc., to appear.
[4] Bedrossian, J., Blumenthal, A., & Punshon-Smith, S. (2019). Almost-sure exponential mixing of passive scalars by the stochastic Navier-Stokes equations. Ann. Prob., to appear.
[5] Bedrossian, J., Blumenthal, A., & Punshon-Smith, S. (2019). The Batchelor spectrum of passive scalar turbulence in stochastic fluid mechanics at fixed Reynolds number. Comm. Pure Appl. Math., to appear. 
[6] Bedrossian, J., Blumenthal, A., & Punshon-Smith, S. (2021). Almost-sure enhanced dissipation and uniform-in-diffusivity exponential mixing for advection-diffusion by stochastic Navier-Stokes. Prob. Theory Rel. Fields, 179(3), 777-834.
[7] Gibson, C.H., & Schwarz, W.H. (1963). The universal equilibrium spectra of turbulent velocity and scalar fields. J. Fluid Mech., 16(3), 365-384.
[8] Grant, H.L., Hughes, B.A., Vogel, W.M., & Moilliet, A. (1968). The spectrum of temperature fluctuations in turbulent flow. J. Fluid Mech., 34(3), 423-442.
[9] Thiffeault, J.-L. (2012). Using multiscale norms to quantify mixing and transport. Nonlin., 25(2), R1-R44.