SIAM News Blog
Research

Updated Equation for FDA Guidance Improves the Accuracy of Drug Interaction Predictions

By

When drugs are absorbed into the body, they are metabolized and removed by enzymes from organs like the liver (see Figure 1a). The presence of other drugs that increase the body’s enzyme secretion may expedite the rate at which a given drug leaves the system (see Figure 1b). This outcome dramatically decreases the drug’s concentration, reducing its efficacy to the point that it may fail to have any effect at all [5]. Therefore, accurately predicting the clearance rate in the presence of drug-drug interaction1 is critical during prescription allotment and drug development.

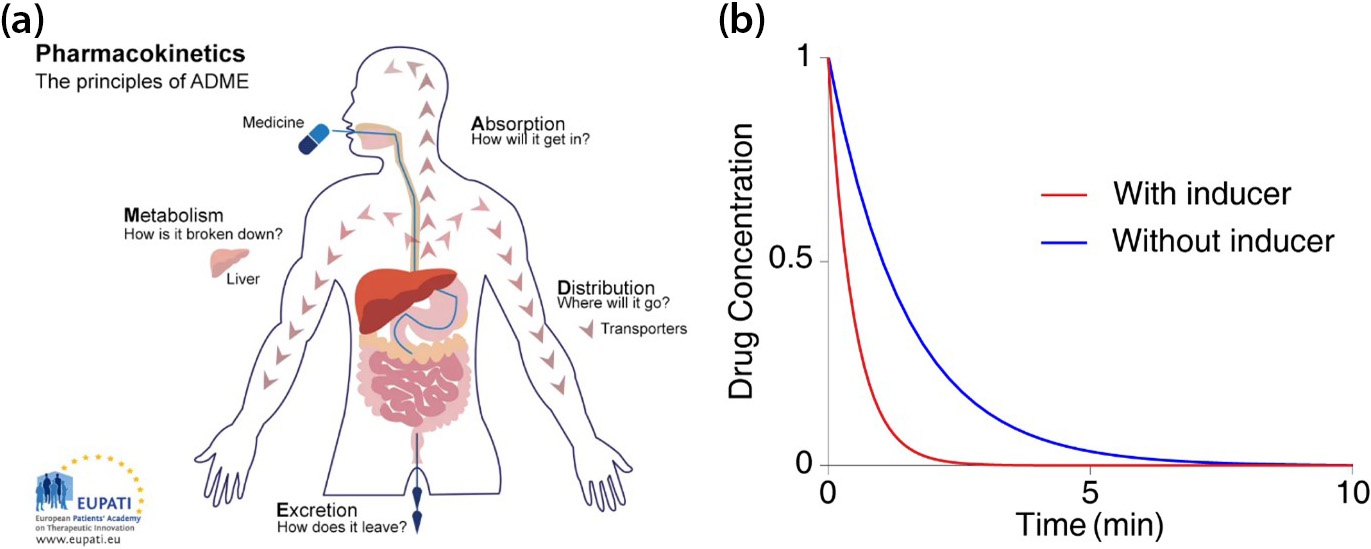
<strong>Figure 1.</strong> The concurrent administration of other drugs can affect the metabolism of a drug in the body. <strong>1a.</strong> Administered drugs are absorbed into the body and distributed to their target sites via the bloodstream. Enzymes—primarily within the liver—then metabolize the drugs, which are eventually excreted through mainly the kidneys. <strong>1b.</strong> In response, the plasma concentration of the drugs gradually declines over time (blue curve). But when inducers are administered together with the drug, they enhance the enzymes’ metabolic activity and accelerate the decline in drug concentration (red curve). Researchers often evaluate such drug interactions by the ratio of the area under the red and blue curves. Figure 1a courtesy of the <a href="https://toolbox.eupati.eu/resources/key-principles-of-pharmacology/" rel="noopener noreferrer" target="_blank">European Patients’ Academy on Therapeutic Innovation</a> and licensed under <a href="https://creativecommons.org/licenses/by-nc-sa/4.0/" rel="noopener noreferrer" target="_blank">CC BY-NC-SA 4.0</a>, Figure 1b courtesy of the authors.
Figure 1. The concurrent administration of other drugs can affect the metabolism of a drug in the body. 1a. Administered drugs are absorbed into the body and distributed to their target sites via the bloodstream. Enzymes—primarily within the liver—then metabolize the drugs, which are eventually excreted through mainly the kidneys. 1b. In response, the plasma concentration of the drugs gradually declines over time (blue curve). But when inducers are administered together with the drug, they enhance the enzymes’ metabolic activity and accelerate the decline in drug concentration (red curve). Researchers often evaluate such drug interactions by the ratio of the area under the red and blue curves. Figure 1a courtesy of the European Patients’ Academy on Therapeutic Innovation and licensed under CC BY-NC-SA 4.0, Figure 1b courtesy of the authors.

It is virtually impossible to evaluate all conceivable interactions between new drug candidates and existing marketed drugs during the development process. As such, the U.S Food and Drug Administration (FDA) recommends a particular formula that indirectly evaluates drug interactions in order to minimize side effects from the simultaneous use of multiple types of drugs (see Figure 2) [2]. The FDA formula, which was first published in 1997 and revised in January 2020, predicts the ratio of the area under the victim drug’s2 plasma concentration-time curve (AUCR) between the presence and absence of the inducer (see Figure 1b):

\[\textrm{AUCR} = \frac{1}{F_g+(1-F_g )\cdot \left( 1+\frac{E_{\textrm{max}} I_g}{I_g+ EC_{50}} \right) } \cdot \frac{1}{f_{m,\textrm{CYP3A4}} \left( 1+ \frac{E_{\textrm{max}} I_h}{I_h+EC_{50}} \right) + (1-f_{m,\textrm{CYP3A4}}) }.\]

<strong>Figure 2.</strong> The title page of the U.S. Food and Drug Administration (FDA) guidance for drug-drug interaction. This guidance recommends several model-based predictions that determine potential drug-drug interactions. Figure courtesy of [2].
Figure 2. The title page of the U.S. Food and Drug Administration (FDA) guidance for drug-drug interaction. This guidance recommends several model-based predictions that determine potential drug-drug interactions. Figure courtesy of [2].

Here, \(I_h\) and \(I_g\) are respectively the unbound concentrations of inducer in the liver and intestine, \(E_{\textrm{max}}\) is the maximal induction effect that is determined in vitro, \(EC_{50}\) is the inducer concentration that causes half of \(E_{\textrm{max}}\), \(F_g\) is the gut availability, and \(f_{m,\textrm{CYP3A4}}\) is the fraction of a substrate that is cleared by the hepatic CYP3A4 enzyme. As the induction effect (i.e., \(1+\frac{E_{\textrm{max}} I}{I+ EC_{50}}\)) increases, both the clearance rate of the victim drug and the AUCR decrease.

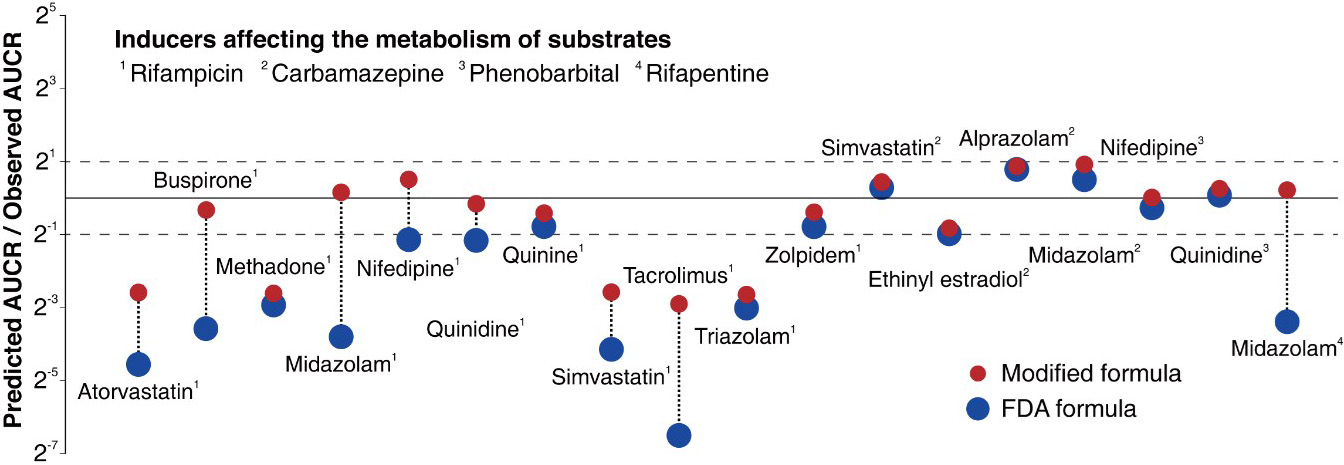
However, the accuracy of the FDA formula has been highly unsatisfactory. In fact, only 38 percent of its predictions have less than two-fold errors (see Figure 3), and previous studies plugged scientifically unjustified constants into the equation to make up for the gap [3]. This strategy is comparable to the introduction of epicyclic orbits to explain the planets’ motion when the now-defunct Ptolemaic theory was the only available interpretation. To address this shortcoming, we identify the major causes of the FDA formula’s inaccuracies and present a solution [9].

The FDA formula relies on the 110-year-old Michaelis-Menten (MM) model [6], which describes the rate of a drug’s metabolism \((S)\) to its product \((P)\): \[\frac{dP}{dt} = \frac{k_{\textrm{cat}} E_T S}{S+K_m} \approx \frac{k_{\textrm{cat}} E_T}{K_m} S,\]

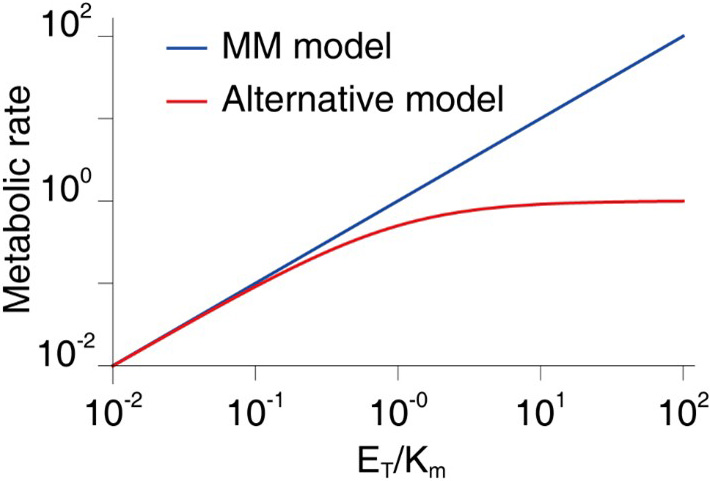
where \(k_{\textrm{cat}}\) is the catalysis reaction rate, \(E_T\) is the enzyme concentration, and \(K_m\) is the MM constant. We ignore \(S\) in the denominator since \(S \ll K_m\) in general. The MM model has a fundamental limit because it makes a very broad and groundless assumption about the presence of the enzymes that metabolize the drug. Though the MM model is one of the most widely-known equations in biochemistry—appearing in more than 220,000 published papers—it is only accurate when the concentration of the enzyme that metabolizes the drug is negligible in comparison to the value of \(K_m\) [4]. In 2020, we found that the concentration of the CYP3A4 enzyme in the liver is much higher than expected and thus comparable with the value of \(K_m\) for many drugs [1]. Furthermore, if the enzyme’s concentration is increased by induction, it is more likely to exceed \(K_m\); the validity condition for the MM model is consequently violated for many more drugs.

<strong>Figure 3.</strong> The modified formula predicts the ratio of the area under the plasma concentration-time curve (AUCR) more accurately than the U.S. Food and Drug Administration (FDA)’s current formula, which highly underestimates the AUCR for numerous inducer-substrate pairs (especially those that contain rifampicin). Here, the blue dots indicate the average AUCR precision with the FDA formula for each inducer-substrate pair, and the red dots denote the modified formula’s results. The solid line and the dashed lines respectively designate the lines of precise prediction and the two-fold error. Figure courtesy of the authors.
Figure 3. The modified formula predicts the ratio of the area under the plasma concentration-time curve (AUCR) more accurately than the U.S. Food and Drug Administration (FDA)’s current formula, which highly underestimates the AUCR for numerous inducer-substrate pairs (especially those that contain rifampicin). Here, the blue dots indicate the average AUCR precision with the FDA formula for each inducer-substrate pair, and the red dots denote the modified formula’s results. The solid line and the dashed lines respectively designate the lines of precise prediction and the two-fold error. Figure courtesy of the authors.

Rather than rely on the MM model, we used an alternative model that more accurately predicts the drug metabolism rate regardless of enzyme concentration [1, 4, 7, 8]:

\[\frac{dP}{dt} = \frac{1}{2} \left\{ (S+K_m+E_T) - \sqrt{(S+K_m+E_T)^2 - 4E_T S} \right\} \approx \frac{k_{\textrm{cat}} E_T S}{E_T+S+K_m} \approx \frac{k_{\textrm{cat}} E_T S}{E_T+K_m}.\]

Here, the first approximation results from the Taylor expansion in terms of \(\frac{4E_T S}{(S+K_m+E_T)^2}\), which is small because \(S \ll K_m\). Note that the denominator contains \(E_T\), unlike the MM model. This difference means that our alternative model predicts finite metabolic rates when \(E_T\) becomes infinite; in contrast, the MM model predicts an unrealistic infinite metabolic rate (see Figure 4). Based on this alternative model, we modified the FDA formula as follows:

\[\textrm{AUCR} = \frac{1}{F_g+(1-F_g) E_{\textrm{ind},G} \frac{E_{T,G}+K_m}{E_{\textrm{ind},G} E_{T,G}+K_m}} \cdot \frac{1}{f_{m,\textrm{CYP3A4}} E_{\textrm{ind},H} \frac{E_{T,H}+K_m}{E_{\textrm{ind},H} E_{T,H}+K_m} +(1-f_{m,\textrm{CYP3A4}})},\]

<strong>Figure 4.</strong> Our alternative model produces a more realistic metabolic rate than the Michaelis-Menten (MM) model. The MM model predicts an unrestricted linear increase in the metabolic rate given an increase in enzyme concentration, while the alternative model more realistically predicts a saturation point for the metabolic rate increment. When \(E_T\) is comparable to or greater than \(K_m\), the two models consequently produce significantly different predictions. The modified formula is therefore superior to the U.S. Food and Drug Administration’s current equation when inducers highly increase the enzyme concentration. Figure courtesy of the authors.
Figure 4. Our alternative model produces a more realistic metabolic rate than the Michaelis-Menten (MM) model. The MM model predicts an unrestricted linear increase in the metabolic rate given an increase in enzyme concentration, while the alternative model more realistically predicts a saturation point for the metabolic rate increment. When \(E_T\) is comparable to or greater than \(K_m\), the two models consequently produce significantly different predictions. The modified formula is therefore superior to the U.S. Food and Drug Administration’s current equation when inducers highly increase the enzyme concentration. Figure courtesy of the authors.

where \(E_{\textrm{ind},g} = 1+ \frac{E_{\textrm{max}} I_g}{I_g+EC_{50}}\) and \(E_{\textrm{ind},h} = 1+ \frac{E_{\textrm{max}} I_h}{I_h+EC_{50}}\). The modified formula dramatically increases the accuracy of the resulting estimates. The existing FDA formula predicts drug interactions within a two-fold margin of error at a rate of 38 percent, whereas the accuracy rate of the modified formula reaches 80 percent (see Figure 3).

We expect that such a drastic improvement in drug-drug interaction prediction accuracy will increase the success rate of new drug development and drug efficacy in clinical trials. As this study’s results were published as a cover article in a top clinical pharmacology journal [9], we hope that FDA guidance will be revised accordingly. Ultimately, this work highlights the importance of collaborative research between groups in vastly different disciplines to further advance the dynamic field of drug interactions.

1 Drug-drug interaction is a phenomenon that occurs when two drugs are taken together, and one drug changes the metabolism of the other to promote or inhibit its excretion from the body. This increases medicine toxicity or lessens efficacy. 

2 The victim drug is the one that is affected by the drug-drug interaction. 

Acknowledgments: We would like to acknowledge our coauthors on this study: Ngoc-Anh Thi Vu, Quyen Thi Tran, Hwi-yeol Yun, Sang Kyum Kim, and Jung-woo Chae (all of Chungnam National University).

References

[1] Back, H.-m., Yun, H.-y., Kim, S.K., & Kim, J.K. (2020). Beyond the Michaelis-Menten: Accurate prediction of in vivo hepatic clearance for drugs with low \(K_M\). Clin. Transl. Sci., 13(6), 1199-1207.
[2] Center for Drug Evaluation and Research. (2020). In vitro drug interaction studies — Cytochrome P450 enzyme- and transporter-mediated drug interactions: Guidance for industry. Silver Spring, MD: U.S. Food and Drug Administration.
[3] Fahmi, O.A., Maurer, T.S., Kish, M., Cardenas, E., Boldt, S., & Nettleton, D. (2008). A combined model for predicting CYP3A4 clinical net drug-drug interaction based on CYP3A4 inhibition, inactivation, and induction determined in vitro. Drug Metab. Dispos., 36(8), 1698-1708.
[4] Kim, J.K., & Tyson, J.J. (2020). Misuse of the Michaelis–Menten rate law for protein interaction networks and its remedy. PLoS Comput. Biol., 16(10), e1008258.
[5] Lin, J.H. (2006). CYP induction-mediated drug interactions: In vitro assessment and clinical implications. Pharm. Res., 23(6), 1089-1116.
[6] Michaelis, L., & Menten, M.L. (1913). Die kinetik der invertinwirkung. Biochem. Zeit., 49, 333-369.
[7] Schnell, S., & Maini, P.K. (2002). Enzyme kinetics far from the standard quasi-steady-state and equilibrium approximations. Math. Comput. Model., 35(1-2), 137-144.
[8] Tzafriri, A.R. (2003). Michaelis-Menten kinetics at high enzyme concentrations. Bull. Math. Biol., 65(6), 1111-1129.
[9] Vu, N.-A.T., Song, Y.M., Tran, Q.T., Yun, H.-y., Kim, S.K., Chae, J.-w., & Kim, J.K. (2023). Beyond the Michaelis-Menten: Accurate prediction of drug interactions through Cytochrome P450 3A4 induction. Clin. Pharmacol. Ther., 113(5), 1048-1057. 

About the Authors

Yun Min Song

Postdoctoral fellow, Institute for Basic Science

Yun Min Song is a postdoctoral fellow in the Biomedical Mathematics Group at the Institute for Basic Science in South Korea. He holds a Ph.D. in mathematical sciences from the Korea Advanced Institute of Science and Technology. Song’s work integrates mathematical modeling, statistical inference, and artificial intelligence to address complex biomedical problems, including pharmacokinetics and the analysis of wearable-device data.

Jae Kyoung Kim

Associate professor, Korea Advanced Institute of Science and Technology

Jae Kyoung Kim is an associate professor in the Department of Mathematical Sciences at the Korea Advanced Institute of Science and Technology and chief investigator in the Biomedical Mathematics Group at the Institute for Basic Science in South Korea. He holds a Ph.D. in applied and interdisciplinary mathematics from the University of Michigan. Kim’s research combines nonlinear dynamics, stochastic processes, and scientific computing to address critical biological and medical problems, including sleep disorders.