What Can Quantum Computers Do for Applied Mathematicians?

As applied mathematicians, we are familiar with the standard model of computation that is embodied by Turing machines. The Church-Turing thesis postulates that any physically realizable computation can be performed by a Turing machine, while the extended version suggests that any such computation can be performed efficiently by a probabilistic Turing machine. Although the original Church-Turing thesis is widely accepted, quantum computers challenge the veracity of the extended version; these computers represent a reasonable, physically realizable model of computation, but we do not yet know whether a probabilistic Turing machine can efficiently simulate them. The general belief is that it cannot, but as with many other fundamental questions in computational complexity theory, this belief may very well be disproven.

Computational Model

On the surface, quantum computers are programmed much like classical (i.e., non-quantum) machines; they have a state that evolves through the application of operations, and they ultimately output some information based on the final state. However, the state, operation, and output components behave differently from their classical counterparts. Here, we concisely describe these components; more details are available in the literature [8].

Let \(\otimes\) denote the tensor product, which is the same as the Kronecker product in this context:

\[A \otimes B = \begin{pmatrix} a_{11} & \dots \\ a_{21} & \dots \\ \vdots & \ddots \end{pmatrix} \otimes B = \begin{pmatrix} a_{11}B & \dots \\ a_{21}B & \dots \\ \vdots & \ddots \end{pmatrix}.\]

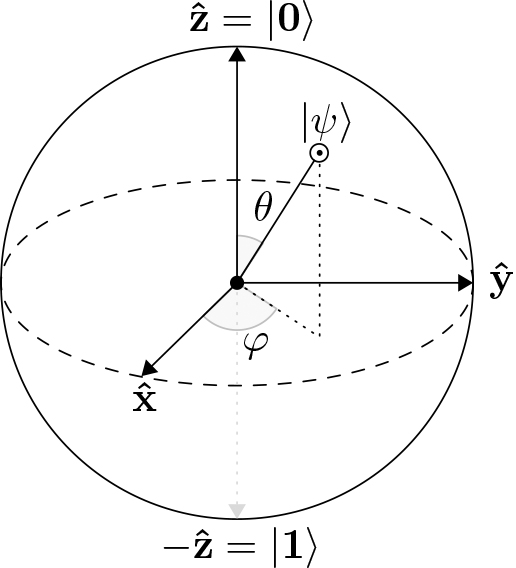
The basic unit of information for a quantum computer is the quantum bit (qubit). The state of a \(q\)-qubit quantum computer is a unit vector in \((\mathbb{C}^{2})^{\otimes q} = \mathbb{C}^{2^q}\). Because this vector space has \(2^q\) standard basis elements, we conventionally label them as \(q\)-digit binary strings that are denoted by \(|j\rangle\) for \(j \in \{0,1\}^q\); a “ket”—i.e., a symbol included in brackets \(|\cdot\rangle\)—is simply a column vector. In quantum mechanics, practitioners often graphically represent a 1-qubit state \(|\psi\rangle = \alpha_0 |0\rangle + \alpha_1 |1\rangle = \alpha_0 \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \alpha_1 \begin{pmatrix} 0 \\ 1 \end{pmatrix}\), \(\alpha_0, \alpha_1 \in \mathbb{C}\) on a sphere (see Figure 1). Such a representation is only up to a global phase factor \(e^{i\phi}\), but this factor is unimportant due to the laws of measurement.

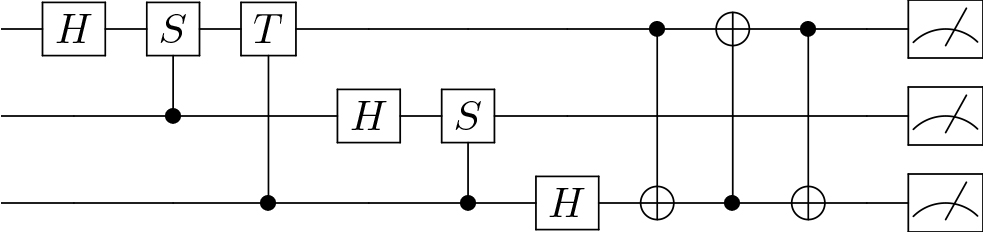
The operations that evolve the state correspond to quantum circuits, which are unitary matrices \(U \in \mathbb{C}^{2^q \times 2^q}\) (see Figure 2). We typically express circuits in terms of basic gates — i.e., certain \(2\times 2\) or \(4\times 4\) complex unitary matrices that constitute the “assembly language.” The composition of basic gates follows the standard rules for tensor products and matrix multiplication. Consider a 2-qubit system; applying the gate \(U\) onto the first qubit and the gate \(V\) onto the second qubit, followed by the gate \(W\) onto the first qubit, is equivalent to applying the matrix \((W\otimes I)(U \otimes V) = WU \otimes V\) to the entire quantum state. A measurement of the state \(|\psi\rangle=\Sigma_{j=0}^{2^q-1} \alpha_j |j\rangle\) is a special, nonunitary operation whose outcome is a random variable \(X\) with sample space \(\{0,1\}^q\) and \(\Pr(X = j) = |\alpha_j|^2\). We only gain information about a quantum state from measurements, and the state collapses to \(|j\rangle\) if we observe \(j\) as the outcome of a measurement.

A quantum algorithm contains quantum circuits and subsequent measurements. In order for a quantum algorithm to be efficient, it must use a polynomial number of resources — i.e., a polynomial number of qubits and basic quantum gates (the assembly language). Based on this explanation, several differences between classical and quantum computers are readily observable. First, describing the state of a quantum computer requires that we specify an exponential-sized complex vector (i.e., \(2^q\) for a \(q\)-qubit system), whereas describing the state of a classical computer simply requires a linear-sized binary vector. But given the effect of measurements, we can only extract a linear amount of information (in terms of the number of qubits) from the exponential-sized complex vector — so from a \(q\)-qubit state, we obtain \(q\) bits of information after a measurement. Second, all operations (except measurements) that a quantum computer applies are linear and reversible; a unitary matrix \(U\) satisfies \(UU^{\dagger} = U^{\dagger}U = I\), where \(\dagger\) denotes the conjugate transpose. Though these properties may seem restrictive, a universal quantum computer is Turing-complete in that it can compute any Turing-computable function while only requiring some polynomial number of additional resources.

Practical Uses of Quantum Computers

From a practical viewpoint, existing quantum computers are still far from faithfully reproducing the ideal model of quantum computation. Nonetheless, the research community has been persistently seeking strong use cases for quantum computers — many of which will resonate with the SIAM community. Here, we present some of the relevant problems. The following list is not exhaustive, nor can it be, as this area of research is highly active; the takeaway is that quantum computers excel at certain tasks and perform poorly at others. Because classical algorithms and quantum computers offer different tradeoffs for many interesting computational problems, researchers often study quantum approaches in search of potential advantages.

Richard Feynman originally proposed the concept of quantum computers to simulate the time evolution of a quantum mechanical system [5]. Mathematically, this idea is akin to implementing a circuit that acts as \(e^{-iHt}\) on the state vector, where the matrix \(H\) and scalar \(t\) are input data. Quantum computers can solve this problem in time polynomial in the number of qubits [2], whereas no efficient classical algorithm has been discovered so far. The problem is “prototypical” for the class of problems that are efficiently solvable by a quantum computer. It finds direct applications in quantum physics and chemistry (i.e., the simulation of quantum dynamics) and is a core component of many quantum algorithms.

Quantum computers can also aptly estimate certain eigenvalues. Consider a \(q\)-qubit unitary \(U\) (recall that \(U\) is a \(2^q \times 2^q\) matrix) and an eigenvector \(|\psi\rangle\) of \(U\). The phase estimation algorithm determines an \(\varepsilon\)-approximation of the eigenvalue of \(|\psi\rangle\) with \(\mathcal{O}(1/\varepsilon)\) applications of \(U\) and a number of gates that is polynomial in \(q\), whereas a classical algorithm would generally need to perform a matrix-vector operation with the (exponentially-sized) matrix \(U\).

There are several quantum algorithms for the solution of linear systems, beginning with seminal work in 2009 [6]. Multiple possible input models are also in use; for example, the sparse oracle access model describes matrix entries via maps that indicate the position of nonzero elements and their values. However, this model is not necessarily the most efficient approach for every scenario. Let \(A \in \mathbb{R}^{m \times m}\), \(b \in \mathbb{R}^{m}\), \(\varepsilon > 0\), and \(z = A^{-1}b\). The natural “quantum encoding” of the solution \(z\) is the state \(|\psi\rangle = \frac{1}{\|z\|} \Sigma_{j=0}^{m-1} z_j |j\rangle\). A quantum linear systems algorithm produces a state \(|\phi\rangle\) so that \(\| |\phi\rangle - |\psi\rangle \| \le \varepsilon\). The runtime of such an algorithm is polylogarithmic in \(m\) but depends (at least linearly) on the linear system’s condition number \(\kappa\) [9]. The fastest known runtime for the sparse access input model is \(\tilde{O}(d \kappa)\) (ignoring all polylogarithmic factors), where \(d\) is the maximum number of nonzero elements in each row of \(A\). 

The overarching purpose of these algorithms for linear systems is to implement the matrix function \(f(x) = 1/x\), which implicitly computes an eigendecomposition of \(A\) and takes the reciprocal of each eigenvalue in the corresponding eigenspace. Two important factors merit consideration in this endeavor. First, we must account for the cost of the oracles that describe the entries of \(A\) and prepare a state encoding \(b\). These oracles can be inexpensive if \(A\) and \(b\) admit efficient algorithmic descriptions, but they may take a time that is proportional to the total number of nonzero elements in less favorable scenarios — resulting in a corresponding increase in runtime. Second, the solution \(z\) cannot be read directly because it is encoded as a quantum state. If we wish to extract a classical description of the solution, we must perform a potentially expensive operation called quantum state tomography [10].

It is also possible to efficiently implement other matrix functions besides the inverse on a quantum computer. This prospect is best understood in the framework of block encodings [7]. A block encoding of a matrix \(A\) is a quantum circuit that, in some subspace, acts on the quantum state as \(A\) (possibly rescaled). While a quantum circuit is always a unitary operation, \(A\) need not be unitary or even square in this case. We can utilize a variety of tactics to implement a block encoding of some given matrix \(A\) in a data-driven way. From this block encoding, we can then implement approximations of polynomial functions of \(A\). The construction of the Gibbs state \(e^{A}/\text{Tr}(e^{A})\) for Hermitian \(A\) is a particularly notable scenario. Gibbs states are important in many branches of applied mathematics, including machine learning and optimization. In some cases, a block encoding of an \(n \times n\) Gibbs state can be constructed in times as fast as \(\mathcal{O}(\sqrt{n})\)! The speedup is quite large compared to classical approaches, although the stated runtime is only achievable under very specific, favorable conditions.

Finally, quadratic quantum speedups via amplitude amplification yield faster algorithms for many problems [3]. One such example is unstructured search (also known as Grover’s algorithm), which searches over a set with no structural property so that the only possible search approach is to examine all of the elements in the set. Another example is mean estimation, which computes the mean of a univariate or multivariate random variable [4]. These approaches are strongly related to quantum walks, which also admit quadratic speedups when compared to classical random walks [1]. The speedups rely on specific input models and may incur additional conditions, so it is important to pay attention to the details.

The aforementioned problems represent only a tiny fraction of active research areas, but hopefully this overview will generate some excitement about quantum computing. Quantum algorithms can be understood purely through linear algebra and often offer different tradeoffs than classical algorithms, which means that they are potentially useful under the right conditions. However, we must overcome many challenges—in subjects such as hardware design and engineering, algorithms and software, and practical considerations like numerical stability—to bring this source of potential to fruition. Classical computers will likely remain the best choice for most computational problems, but if quantum computers can accelerate even just a few key issues in practice, that alone could be worth the time and exploratory investment.

References

[1] Apers, S., Gilyén, A., & Jeffery, S. (2019). A unified framework of quantum walk search. Preprint, arXiv:1912.04233.
[2] Berry, D.W., Childs, A.M., & Kothari, R. (2015). Hamiltonian simulation with nearly optimal dependence on all parameters. In 2015 IEEE 56th annual symposium on foundations of computer science (pp. 792-809). Berkeley, CA: Institute of Electrical and Electronics Engineers.
[3] Brassard, G., Høyer, P., Mosca, M., & Tapp, A. (2002). Quantum amplitude amplification and estimation. In S.J. Lomonaco, Jr. & H.E. Brandt (Eds.), Quantum computation and information (pp. 53-74). Contemporary mathematics (Vol. 305). Providence, RI: American Mathematical Society.
[4] Cornelissen, A., Hamoudi, Y., & Jerbi, S. (2022). Near-optimal quantum algorithms for multivariate mean estimation. In STOC 2022: Proceedings of the 54th annual ACM SIGACT symposium on theory of computing (pp. 33-43). Rome, Italy: Association for Computing Machinery.
[5] Feynman, R.P. (1982). Simulating physics with computers. Int. J. Theor. Phys., 21(6/7), 467-488.
[6] Harrow, A.W., Hassidim, A., & Lloyd, S. (2009). Quantum algorithm for linear systems of equations. Phys. Rev. Lett., 103(15), 150502.
[7] Lin, L. (2022). Lecture notes on quantum algorithms for scientific computation. Preprint, arXiv:2201.08309.
[8] Nielsen, M.A., & Chuang, I.L. (2010). Quantum computation and quantum information (2nd ed.). Cambridge, U.K.: Cambridge University Press.
[9] Somma, R.D., & Subaşı, Y. (2021). Complexity of quantum state verification in the quantum linear systems problem. PRX Quantum, 2(1), 010315.
[10] Van Apeldoorn, J., Cornelissen, A., Gilyén, A., & Nannicini, G. (2023). Quantum tomography using state-preparation unitaries. In Proceedings of the 2023 annual ACM-SIAM symposium on discrete algorithms (SODA) (pp. 1265-1318). Philadelphia, PA: Society for Industrial and Applied Mathematics.