What is Entropy?

A short and clear answer to the question in the title of this article may be difficult to find (at least, it was for me). I would therefore like to illustrate the entropy of gas on the simple parody of ideal gas: a single particle—a “molecule”—that bounces elastically between two stationary walls. To strip away the remaining technicalities, let’s take the molecule’s mass as \(m=1\). Our system has one degree of freedom \(n=1\) (as opposed to \(n=3\) in a monatomic gas).

Entropy in One Sentence

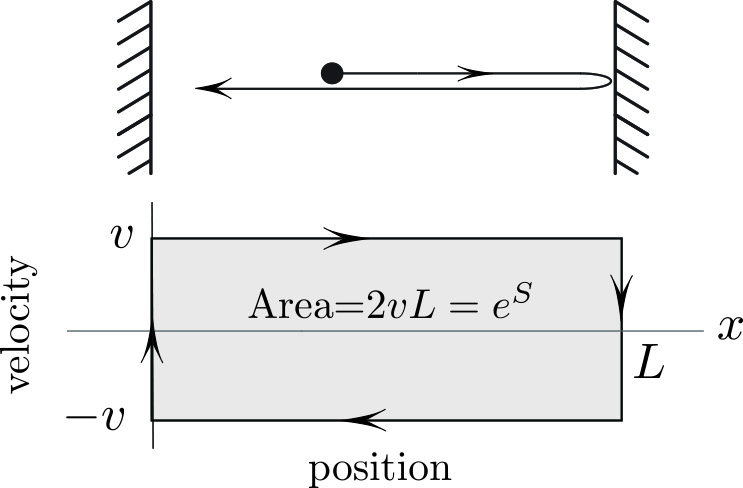
The phase plane trajectory of the particle in Figure 1 is a rectangle with area \(2vL\). The entropy \(S\) of the “gas” in Figure 1 is the logarithm of the area inside the phase plane trajectory:¹ 

\[S = \ln (\hbox{area}) = \ln ( 2vL). \tag1 \]

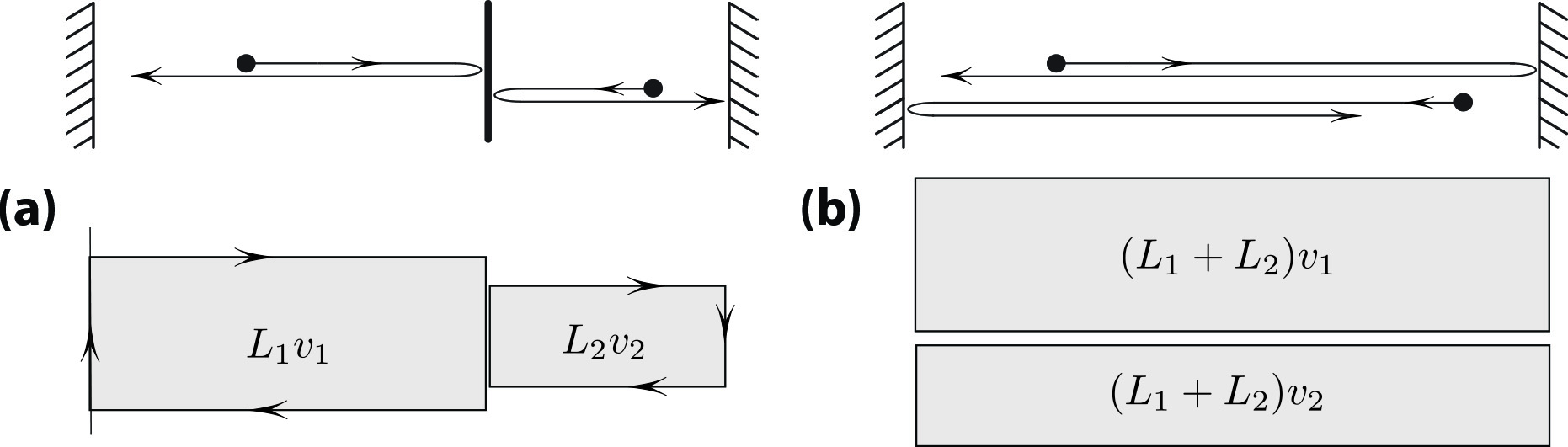
Taking the log in \((1)\) is a natural (apologies for the pun) choice. For one, it makes the entropy additive. Indeed, consider a system that consists of two “vessels” with lengths \(L_1\), \(L_2\) and speeds \(v_1\), \(v_2\) (see Figure 2a). The phase space is now the Cartesian product \(\{(x_1,v_1; x_2, v_2\})\). The four-dimensional volume of the Cartesian product of two rectangles is \(2v_1L_12v_2 L_2= \hbox {Area}_1\hbox {Area}_2\); the logarithm of the product is thus \(S=S_1+S_2\).

Another motivation for taking the logarithm is that it makes the entropy in \((1)\) analogous to Shannon’s entropy. Roughly speaking and in the simplest setting, this latter form of entropy counts the number of letters in a word; this number is then the logarithm of the number of possible words.² The area in Figure 1 is the most natural measure of the number of possible states, thus making \(S\) a continuous analog of Shannon’s entropy.

If we add a small amount \(dQ\) of heat to the gas at temperature \(T,\) why does the entropy change according to

\[dS = \frac{dQ}{T}, \tag2\]

the standard formula in most physics textbooks? Feynman’s beautiful lectures explain \((2)\) in a more realistic setting but take several pages, so here is a quick explanation of \((2)\) in our simple case.

Explanation of (2)

Let’s add heat \(dQ\) by increasing the kinetic energy of the molecule in Figure 1, which amounts to increasing \(v\):

\[dQ=d( v ^2 /2) = v\; dv. \tag3\]

The change \(dv\) in turn causes \(S = \ln (2vL)\) to change:

\[dS \stackrel{(1)}{=}  \frac{dv}{v} = \frac{vdv}{v ^2 } \stackrel{(3)}{=}  \frac{dQ}{v^2} = \frac{dQ}{T},\]

where the “temperature”

\[T= v ^2 \tag4\]

is twice the kinetic energy of the molecule. I put “temperature” in quotes because it is measured in units of energy rather than degrees. The coefficient that relates the two units is called the Boltzmann constant.

Boltzmann Constant

We can measure the temperature of a gas in units of average kinetic energy of a molecule³ per degree of freedom, or in Kelvin degrees. The coefficient between these two measures is called the Boltzmann constant \(k_B\):

\[\frac{1}{n} mv ^2 = k_B \;T,\]

where \(n\) is the number of degrees of freedom and \(T\) is in Kelvin units. To put it differently, \(k_B\) is the kinetic energy per molecule per degree of freedom that is required to raise the temperature by \(2^\circ \textrm{K}\). Not surprisingly, it is a tiny number: \(k_B \approx 1.4 \times  10^{-23} \textrm{J/K}\) (joules per Kelvin). The units of temperature in \((4)\) are the same as those of kinetic energy, so "\(k_B\)"\(\,=1\) (and also \(n=1\)) in that case.

Entropy Increase

When two substances are mixed, the entropy of the mixture is greater than the sum of the original entropies:

\[S_{\hbox{mixture}}> S_1+S_2.\]

For our one-dimensional gas, this statement borders on triviality. Indeed, consider two side-by-side vessels (see Figure 2). Removing the wall does not affect the speeds but does increase the “volume,” which becomes \(L=L_1+L_2\) so that

\[S_{\hbox{before}}=\ln(L_1v_1) + \ln(L_2v_2) < \ln(Lv_1)+ \ln(Lv_2) = S_{\hbox{after} }.\]

Adiabatic Processes

All thermodynamics textbooks mention that entropy does not change during adiabatic processes.⁴ For our “gas,” this amounts to the following rigorously proved statement: If the length \(L =L( \varepsilon t)\) changes smoothly over the time interval \(0\leq t\leq 1/ \varepsilon\), then the product \(Lv\) changes by the amount \(O (\varepsilon)\) if \(\varepsilon\) is sufficiently small.

This basic example captures the essential mechanism and the reason for adiabatic invariance of entropy in ideal gases. However, no rigorous proof of adiabatic invariance exists — even for the simplest system of two “molecules” that are modeled by hard disks bouncing inside of a square with slowly moving walls. The gap between what we believe and what we can actually prove is enormous.

In conclusion, it seems that discussions of entropy—at least on simple phase plane examples like the one here—belong in dynamical systems textbooks (and in physics texts when entropy is mentioned).

¹ The same definition applies to the actual gas; in that case, the area is replaced by the volume that is enclosed by the energy surface in the phase space. The dimension of this space is enormous, and the volume must be measured in appropriate units.

² As long as we allow all possible combinations of letters, and each letter is equally probable.

³ Twice the kinetic energy as in \((4)\).

⁴ I.e., a slow change of vessel with no heat or mass exchange with the outside.

The figures in this article were provided by the author.