Where Algebra and Geometry Meet Systems Biology

Researchers often use mathematical models to investigate systems of interacting species across scientific fields such as chemistry, population biology, molecular biology, and epidemiology. Here, we will concentrate on algebra and geometry’s beautiful relationship with systems biology in the context of biochemical reaction networks that use systems of ordinary polynomial differential equations. This modeling approach, which is based on the law of mass-action kinetics, is typically applicable when molecules are abundant and different chemical species are well mixed. Other techniques—including stochastic and partial differential equation models—find use under different sets of assumptions, while machine learning is the subject of current exploration.

The input information for a chemical reaction network is a finite set of \(n\) species and a directed graph that represents a finite set of \(r\) reactions among these species. Variables \((x_1, \dotsc x_n)\) in the polynomial dynamical system correspond to the different species’ concentrations; the solutions of the dynamical system are curves in the nonnegative orthant in \(\mathbb{R}^n\) that describe the evolution of these concentrations over time. The polynomials have a combinatorial structure that is read from the digraph of reactions and involves \(p\) parameters, which are frequently unknown and can vary across individuals and environmental conditions. Surveys in the literature provide exact definitions, further references, and precise formulations of important signaling pathways [5-7].

Classical applications attempt to build models that reproduce data. The primary objective of reaction network theory is to understand these models’ dynamics across different parameter values and ascertain whether specific phenomena—like bistability or oscillations—can manifest under appropriate parameter choices. A particular type of parameter values are the reaction rate constants \(\kappa = (k_1, \dots, k_r)\) that are associated with each reaction. In the presence of mass-action kinetics, each reaction’s velocity is proportional to the product of the reactant concentrations and the corresponding reaction rate constant. Because linear conservation relations appear naturally in most signaling pathways, the trajectories over an interval are constrained to linear varieties that are parallel to the stoichiometric subspace \(S\). If \(S\) is cut out by linear equations \(\ell_1(x)= \dotsc = \ell_s(x)=0\), a trajectory is then contained in the linear variety \(\ell_1(x)=T_1, \dotsc = \ell_s(x)=T_s\) for some choice \(T=(T_1, \dots, T_s)\) that is determined by the initial conditions. These parameter values are called the total amounts. In this setting, we must understand the system’s stoichiometrically compatible steady states (SCSSs), which are the joint solutions of the system

\[f_1(\kappa, x) = \dotsc = f_n(\kappa,x) = \ell_1(x)-T_1 = \dotsc = \ell_s(x)-T_s = 0,\]

where the differential equations are denoted by \(\dot{x_i} = f_i(\kappa,x), \ i=1 \dots, n\). We are especially interested in the nonnegative or positive solutions of the algebraic varieties that these polynomials define. Trajectories do not need to converge, but if they do, the limit point is a steady state that is typically stable. Unstable steady states give rise to interesting dynamics.

We can partition the parameter space of the variables \((\kappa, T)\) into semialgebraic sets (defined by polynomial equalities and inequalities with real coefficients) such that the solutions’ qualitative behavior is the same in each region. While many theoretical results and computational tools already exist, the high number of variables and parameters in even the smallest biochemical reaction networks forces us to understand the structure of the systems and pursue novel theoretical and computational results. For instance, the extracellular signal-regulated kinase (ERK) pathway is a cascade of cell protein phosphorylations that communicates a signal from a surface receptor through the membrane and eventually to the DNA in the cell’s nucleus [13]. In a cascade, one layer’s phosphorylated substrate acts as the next layer’s enzyme. Figure 1 corresponds to a reaction network with \(n=22\) variables—eight substrates, four enzymes, and ten intermediate species—in 30 reactions with seven linearly independent conservation relations with \(p = 30 + 7\) parameters, which makes a total of 57 variables. This number is beyond the capability of current computer algebra systems. However, recent studies have used tools from algebra, geometry, and combinatorics to generate many new results about the associated family of polynomial dynamical systems.

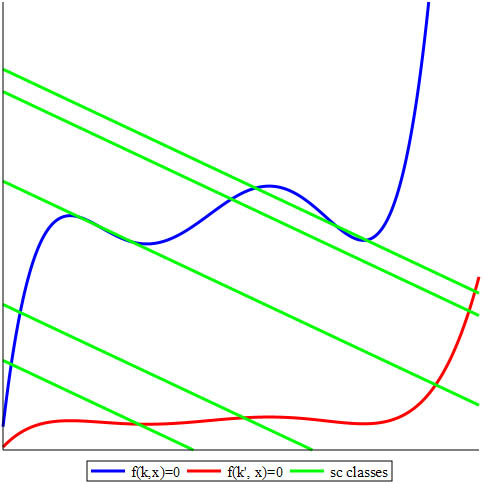
The blue and red curves in Figure 2 represent the zero sets of \(f(\kappa,x)\) and \(f(\kappa', x)\) for different values of the rate constants, and the green lines represent linear varieties that are associated with different values of the total amounts \(T\). Small values of positive \(T\) yield a single intersection with the blue curve. But as \(T\) increases, we alternate between one and three positive steady states; large \(T\) again has consistently only one value. If the curves were more blended, even more SCSSs could exist for some choices of parameters. On the other hand, only a single intersection point is present between the red curve and each green line for any value of \(T\). If there are at least two points of intersection (steady states) in the positive orthant, then the system has the capacity for multistationarity and the corresponding vector of parameters \((\kappa, T)\) is multistationary.

The occurrence of multistationarity is necessary for multistability, i.e., the presence of at least two different stable SCSSs. Multistability is associated with cell differentiation and the manifestation of phenotypic differences under the same genetic or environmental conditions. Because steady states under inspection are usually implicit, the standard methods of stability study require further extensions.

In 1988, Bruce Clarke proposed an interesting point of view called stoichiometric network analysis that only accounts for the parameters \(\kappa\) [3]. Even when it is impossible to parametrize the solutions of \(f_i(\kappa, x)=0, \ i =1\dots,n\) for a fixed value of \(\kappa\), Clarke observed that one can parametrize the values of \((\kappa, x) \in \mathbb{R}^{r+n}_{>0}\) that satisfy these parametric equations in terms of generators of an explicit positive cone that is read from the reactions. This method is algorithmic, though it may be difficult to compute for non-simplicial cones. Our approach uses algebro-geometric tools to understand the structure of these polynomials in biologically meaningful examples. One such class of underlying structures are the Modifications of type Enzyme-Substrate or Swap with Intermediates (MESSI) networks that encompass the most popular models in systems biology, including important enzymatic networks [14].

We prove general results that—under easily checkable combinatorial conditions on the directed graph that represents the network—allow us to preclude relevant boundary steady states, thus implying that the trajectories avoid the boundary of the positive orthant. These results also permit us to determine whether the system is conservative (and trajectories are defined for any \(t \ge0\)); provide an explicit basis of conservation relations; guarantee the rationality of the steady state variety (e.g., the blue or red curve in Figure 2), which means that it can be explicitly parametrized (a very unusual property of general algebraic varieties); and—in many interesting cases—give explicit binomials that cut out the steady state variety and monomials in the concentrations that parametrize it. Using tools from the theory of toric varieties and Gale duality, we demonstrate decisions about multistationarity based on the oriented matroids that are associated with the system’s exponents and coefficients [12]; we also state the first multivariate generalization of the beautiful Descartes’ rule of signs, which René Descartes described in 1634 for univariate real polynomials.

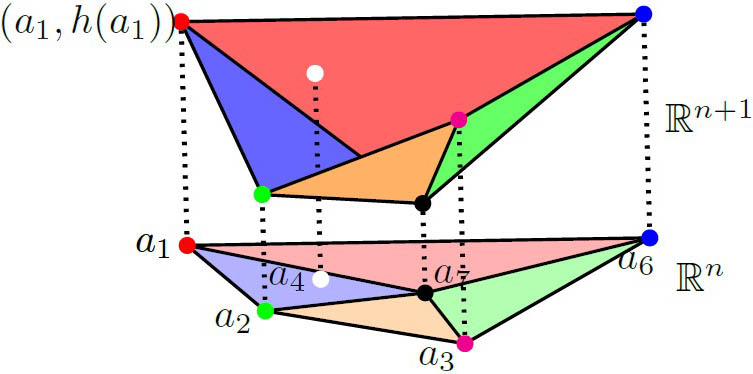
Another algebro-geometric technique with biological applications is the toric degeneration for real solutions. Given a polynomial system with exponents (represented by the dots in Figure 3) and any lifting function \(h\) that is defined on the set \(A\) of exponents, the projection of the lifted points’ lower hull defines a regular subdivision of \(A \textrm{'s}\) convex hull. If the signs of minors of the matrix of system coefficients that correspond to \(q\) simplices in the subdivision satisfy certain conditions, we can find an open set in the full space of parameters \((\kappa, T)\) that guarantees the existence of at least \(q\) SCSSs. It is surprising that these conditions—which are dictated by the combinatorics of the exponents—are generally interpretable in terms of the biochemistry. Further research has applied the basic theory to different enzymatic mechanisms with MESSI structures, even when the dimension is high [2].

In addition to efforts that utilize singular perturbation theory to investigate multistationarity [9], a recent approach relies on combinatorial tools [8] to comprehend the connectivity of regions wherein a given polynomial is negative in the positive orthant of the \(\kappa\) variables, which is related to the regions of multistationarity. While many studies examine the occurrence and inheritance of oscillations, certain results demonstrate that understanding the oscillation capacity from the network’s structure is not a straightforward process [1]. In 1972, Fritz Horn and Roy Jackson proposed an important open conjecture [11]—currently known as the global attractor conjecture—about the dynamics of particular chemical reaction networks [4]. It concerns complex balanced networks, which contain the more classical detailed balanced networks. In this case, there exists a single positive steady state with fixed total amounts that is a local attractor; Horn and Jackson conjectured that it is indeed a global attractor of the dynamics [11]. While the conjecture certainly seems true at first, it has thus far yielded only partial results. Ultimately, however, the union of algebra, geometry, dynamical systems, and biochemistry can undoubtedly drive new theoretical results in both the application domain and the realm of real algebraic geometry.

References
[1] Banaji, M., Boros, B., & Hofbauer, J. (2024). Oscillations in three-reaction quadratic mass-action systems. Stud. Appl. Math., 152(1), 249-278.
[2] Bihan, F., Dickenstein, A., & Giaroli, M. (2020). Lower bounds for positive roots and regions of multistationarity in chemical reaction networks. J. Algebra, 542, 367-411.
[3] Clarke, B.L. (1988). Stoichiometric network analysis. Cell Biochem. Biophys., 12, 237-253.
[4] Craciun, G., Dickenstein, A., Shiu, A., & Sturmfels, B. (2009). Toric dynamical systems. J. Symb. Comput., 44(11), 1551-1565.
[5] Dickenstein, A. (2016). Biochemical reaction networks: An invitation for algebraic geometers. In J.A. de la Peña, J.A. López-Mimbela, M. Nakamura, & J. Petean (Eds.), Mathematical Congress of the Americas (pp. 65-83). Contemporary mathematics (Vol. 656). Providence, RI: American Mathematical Society.
[6] Dickenstein, A. (2019). Algebra and geometry in the study of enzymatic cascades. In C. Araujo, G. Benkart, C.E. Praeger, & B. Tanbay (Eds.), World women in mathematics 2018: Proceedings of the first world meeting for women in mathematics (WM)² (pp. 57-81). Association for Women in Mathematics series (Vol. 20). Cham, Switzerland: Springer.
[7] Dickenstein, A. (2020). Algebraic geometry tools in systems biology. Not. Am. Math. Soc., 67(11), 1706-1715.
[8] Feliu, E., & Telek, M.L. (2022). On generalizing Descartes’ rule of signs to hypersurfaces. Adv. Math., 408(A), 108582.
[9] Feliu, E., Walcher, S., & Wiuf, C. (2022). Critical parameters for singular perturbation reductions of chemical reaction networks. J. Nonlinear Sci., 32(6), 83.
[10] Giaroli, M., Bihan, F., & Dickenstein, A. (2018). Regions of multistationarity in cascades of Goldbeter-Koshland loops. J. Math. Biol., 78, 1115-1145.
[11] Horn, F., & Jackson, R (1972). General mass action kinetics. Arch. Rational Mech. Anal., 47, 81-116.
[12] Müller, S., Feliu, E., Regensburger, G., Conradi, C., Shiu, A., & Dickenstein, A. (2015). Sign conditions for injectivity of generalized polynomial maps with applications to chemical reaction networks and real algebraic geometry. Found. Comput. Math., 16(1), 69-97.
[13] Patel, A.L., & Shvartsman, S.Y. (2018). Outstanding questions in developmental ERK signaling. Development, 145(14), dev143818.
[14] Pérez Millán, M., & Dickenstein, A. (2018). The structure of MESSI biological systems. SIAM J. Appl. Dyn. Syst., 17(2), 1650-1682.