A Simple Explanation of Adiabatic Invariance
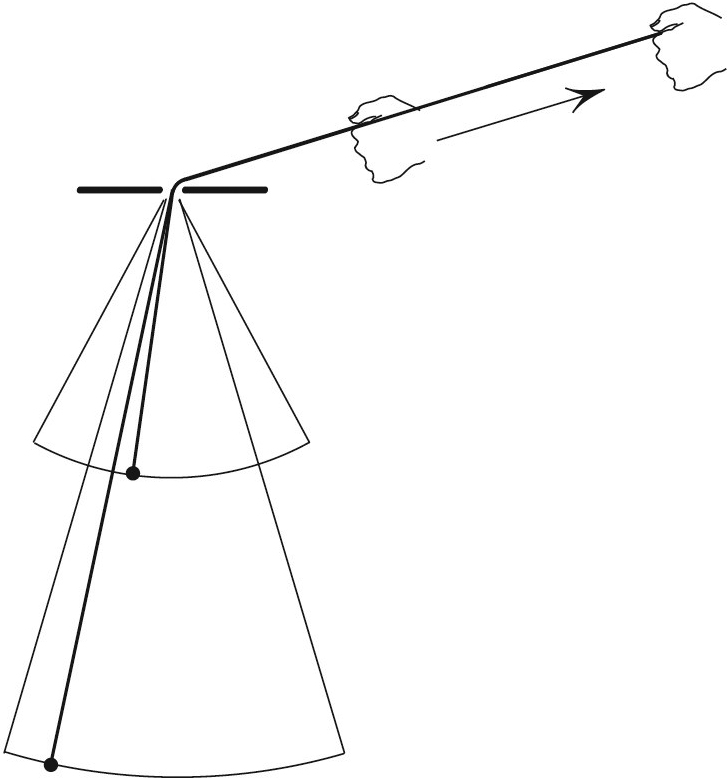
In the early days of quantum mechanics, there was a sense of wonder that the energy-to-frequency ratio of an atom’s radiation is (Planck’s) constant, despite external disturbances. Einstein proposed a classical analog of this phenomenon: If we retract the string of an oscillating pendulum (i.e., the “atom”) slowly and smoothly, then the energy-to-frequency ratio \(E/\omega\) remains nearly constant (see Figure 1). Einstein’s heuristic justification of the near-constancy of \(E/\omega\) is based on the following nice idea [2]. The tension of the string averaged over a full swing is a bit more than the bob’s weight. As we pull the string in, we thus do a bit more work than simply elevating the bob; this extra work becomes added oscillatory energy. Translating the previous sentence into the statement \(E/\omega\approx \textrm{const}.\) requires about a page of calculation [2]; a rigorous proof takes considerably longer [1].
A justification of adiabatic invariance that is much shorter than Einstein’s explanation—but also heuristic—recently occurred to me. The main point is the observation that the pendulum’s adiabatic invariant \(E/\omega\) is approximately the angular momentum of another pendulum, of which our given pendulum is a shadow. But the angular momentum of the counterpart pendulum is conserved exactly, which means that \(E/\omega\) is conserved approximately.
At the root of the derivation of \(E/\omega\approx \textrm{const}.\) is the following trivial observation: For a circular motion of a point mass \(m=1\) with angular velocity \(\omega\) and kinetic energy \(E\), the angular momentum
\[AM = 2 \frac{E}{\omega}.\]
Indeed, \(AM = r ( \omega r) = \omega r ^2\) and \(E= \frac{1}{2} \omega ^2 r ^2\). If the motion is approximately circular, then
\[AM \approx 2 \frac{E}{\omega}.\tag1\]
Justification of \(E/\omega\approx \textrm{const}.\)
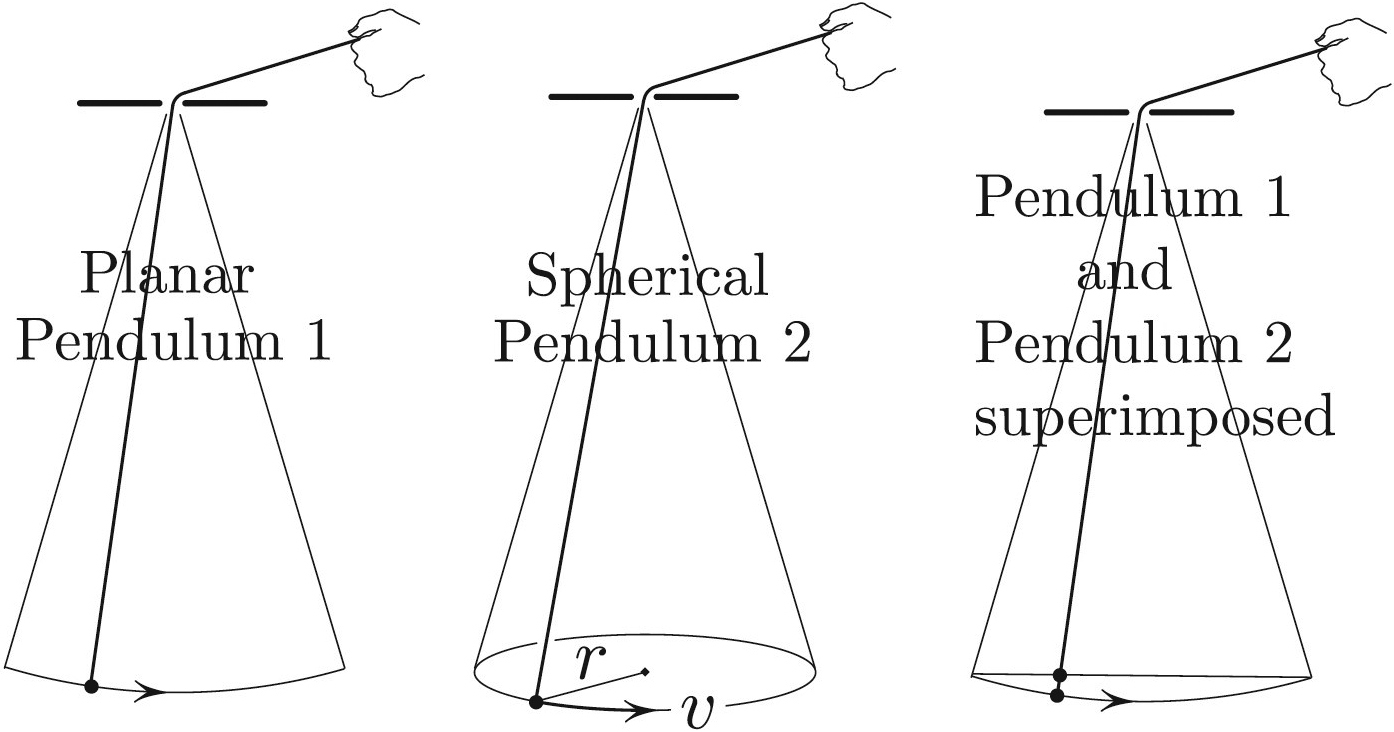
Along with planar pendulum 1 in Figure 2, consider a spherical pendulum 2 of the same length that rotates in the horizontal circle of radius \(r\) that is equal to the amplitude of pendulum 1. Let us now retract both pendulums identically (see Figure 1). For pendulum 2, \(AM = \textrm{const}.\), where \(AM\) is the angular momentum around the vertical line through the suspension point; indeed, the torque around that line is zero. Moreover, pendulum 2 continues to move in a near-circular orbit if we retract slowly, so that the key observation in \((1)\) applies:
\[AM\approx 2 \frac{E_2}{\omega_2 }.\]
The subscripts refer to pendulum 2, where \(E_2\) is the kinetic energy. So, we’ve already found (modulo some rigor) an adiabatic invariant for pendulum 2! But \(E_2 \approx E_1\), where \(E_1\) is the total (kinetic \(+\) potential1) energy of pendulum 1, and \(\omega _1\approx \omega _2\) if we assume small oscillations, so that \(2 \frac{E_1}{\omega_1} \approx AM= \textrm{const}.\) This concludes our heuristic explanation.
1 Potential energy is counted as zero at the bottom point of the pendulum’s swing.
The figures in this article were provided by the author.
References
[1] Arnold, V.I. (1989). Mathematical methods of classical mechanics (2nd ed.). In Graduate texts in mathematics (Vol. 60). New York, NY: Springer.
[2] Nakamura, K. (1993). Quantum chaos: A new paradigm of nonlinear dynamics. In Cambridge nonlinear science series (Vol. 3). Cambridge, UK: Cambridge University Press.
About the Author
Mark Levi
Professor, Pennsylvania State University
Mark Levi (levi@math.psu.edu) is a professor of mathematics at the Pennsylvania State University.
Related Reading
Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



