Geometry of the Phase Lag

Standard sophomore discussions of forced linear oscillations tend to rely on formulas, often without intuitive answers to some of the following basic questions:

1. Why does the phase lag \(\varphi\) lie between \(0\) and \(\pi\) for damped oscillators?
2. Why is \(\varphi =  0\) or \(\pi\) in the absence of damping?
3. Why is \(\varphi =  \pi /2\) when \(\omega = \omega_0\), the natural frequency (i.e., the frequency of the same oscillator without damping)?

All of these questions refer to the harmonic oscillator with viscous drag and subject to sinusoidal forcing:

\[\ddot x + c \dot x + \omega _0 ^2  x = F \cos \omega t, \tag1\]

where \(\omega_0^2 = k\) is Hooke’s constant. We chose mass \(m=1\) without a loss of generality. As a standard step, one complexifies \((1)\), i.e., considers \(x\) as the coordinate of point \(z\) in the plane satisfying

\[\ddot z + c \dot z + \omega_0 ^2  z = F e^{i \omega t}. \tag2\]

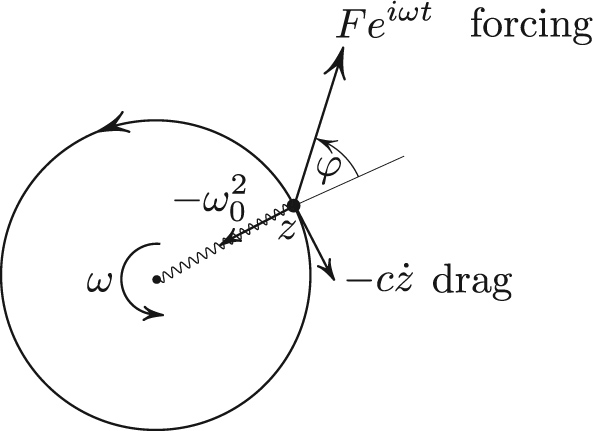
Since complex numbers may spook some students, we can equivalently say that \(x\) in \((1)\) is the \(x\)-coordinate of the point mass that is pulled by the Hookean spring with force \(- \omega_0^2 z\) towards the origin, also subject to both the drag force \(-c \dot z\) that is linear in velocity and the external force of constant magnitude \(F\) that spins with angular velocity \(\omega\), like a spinning jet engine attached to the mass.

The steady state solution of \((1)\) corresponds to the circular motion of the point mass, and the phase lag \(\varphi\) in Figure 1 is the angle by which the direction of response \(z\) lags behind the direction of the forcing. Figure 1 answers the aforementioned questions 1-3 as follows:

1. In the presence of damping, the tangential component \(F \sin \varphi\) must be positive to compensate the drag, hence \(\varphi \in (0,  \pi )\).
2. In the undamped case \(c=0\), the tangential component of forcing must vanish so that \(\varphi = 0\) or \(\pi\); otherwise, the particle will have nonzero tangential acceleration and be unable to maintain constant speed.
3. The case \(\varphi =  \pi /2\) amounts to purely tangential forcing. Since the drag is also tangential and the speed of circular motion is constant, the forcing exactly cancels the drag. We can then pretend that neither drag nor forcing is present; what’s left is a circular motion of the undamped unforced oscillator with Hooke’s constant \(\omega_0 ^2\) and hence with frequency \(\omega_0\). But the frequency of our circular motion is also \(\omega\), so that \(\omega = \omega _0\). Thus, \(\omega = \omega _0\) is equivalent to \(\varphi =  \pi /2\).

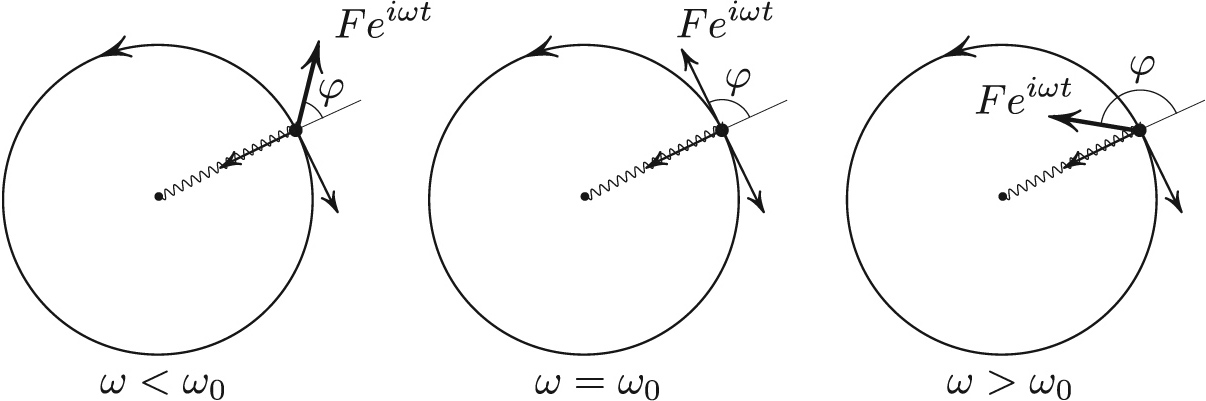
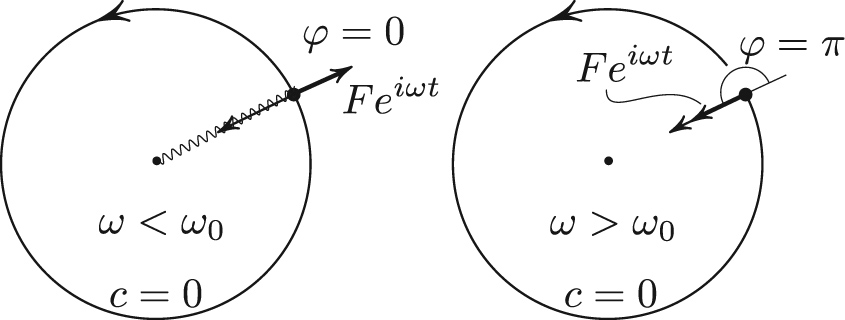
Figures 2 and 3 illustrate several additional properties that are stated and explained in the respective captions.

I deliberately avoided calculations, which are typically done via complex numbers. These calculations are actually made redundant through the use of Newton’s second law: from Figure 1,

\[\begin{eqnarray}F \sin  \varphi &=& c \omega R \cr \\ F \cos \varphi &=& \omega ^2 R- \omega_0 ^2 R. \end{eqnarray}\]

The first equation expresses the balance between the tangential component of forcing and the drag, thus assuring constant speed along the circle. The second equation states that the centripetal force \(\omega ^2 R\) is the resultant of the spring force and the radial component of the driving force.

The lag \(\varphi\) and amplitude \(R\) come out of these formulas, but my goal was to instead gain some insight into phase lag without calculation.

The figures in this article were provided by the author.