Population Dynamics and the Tragedy of the Commons

The harvesting of natural resources has been a key factor in the economic development of societies across the globe. While sustainability was often not a major point of concern, the last 150 years have seen much debate about overfishing’s detrimental impact on renewable fishery resources. During London’s International Fisheries Exhibition in 1883, biologist Thomas Henry Huxley posed the topic of fishery depletion. Though he acknowledged the possible exhaustion of certain fisheries, he also argued that many types of fish were seemingly unlimited in number. “I believe that it may be affirmed with confidence that, in relation to our present modes of fishing, a number of the most important sea fisheries, such as the cod fishery, the herring fishery, and the mackerel fishery, are inexhaustible,” he said. “Any attempt to regulate these fisheries seems consequently, from the nature of the case, to be useless” [7].

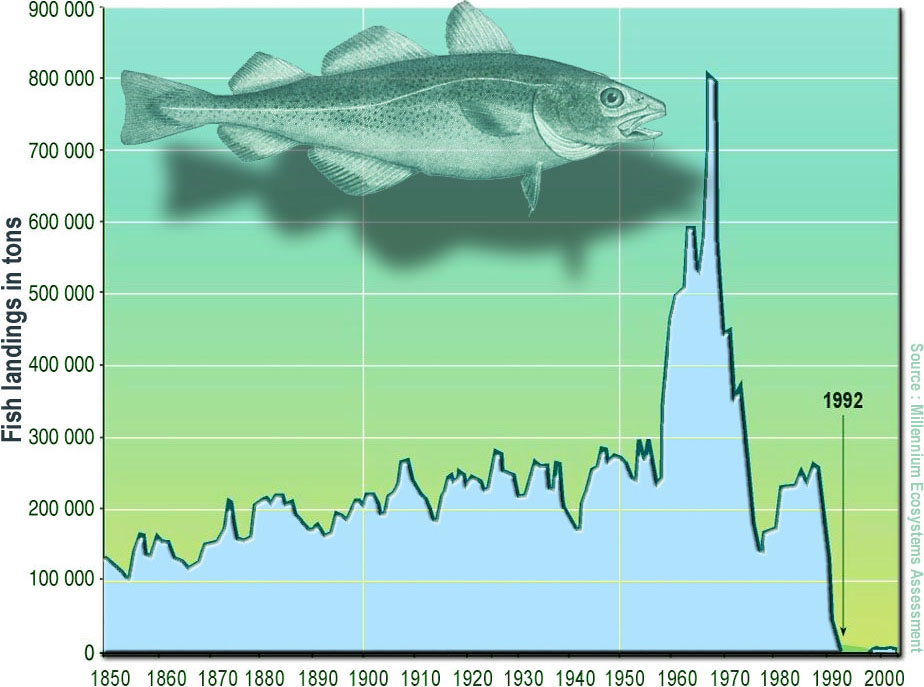
Driven by an ever-growing demand for seafood, global fishing efforts escalated dramatically during the 20th century. This increase resulted in numerous well-documented instances of overfishing and species depletion worldwide that were characterized by an unexpectedly rapid and severe decline in fish landings over a short time period. The collapse of Atlantic cod stocks in 1992 serves as a stark illustration of this phenomenon (see Figure 1).

Overfishing has a rational behavioral component that ecologist Garret Hardin explained in his celebrated 1968 essay titled “The Tragedy of the Commons” [5]. Simply put, the tragedy of the commons is a situation wherein individuals with access to a shared public resource act in their own best interests and ultimately deplete the resource. Hardin framed the scenario as an adaptation of the prisoner’s dilemma, which offers a compelling quantitative interpretation of the impact of aggregated harvesting behaviors on the overall fish population.

To address spatial phenomenology, one must represent the fish population as a density that is distributed across a spatial domain; blend it with population dynamics models; and include local interactions between fish, fishers, and their environment. A natural approach that encapsulates space dependence—as well as death and reproduction—is a reaction-diffusion equation that takes the following form:

\[\partial_t\theta-\partial_{xx}\theta=f(\theta),\]

where \(f\) is a nonlinearity that models intraspecific phenomena like death and reproduction. 

Ronald Fisher, Andrey Kolmogorov, Ivan Petrovsky, and Nikolai Piskunov studied the so-called traveling wave solutions to this type of equation in the 1930s [4, 10]; Paul Fife and John Bryce McLeod later examined the same phenomena in the 1970s [3]. Traveling wave solutions take the form of \(\theta(x,t)=\Theta(x-ct)\) and are of paramount importance; in many situations, generic solutions of reaction-diffusion equations resemble such traveling waves. In recent years, much research on invasive species control has focused on these equations and their particular solutions [1]. In fact, Alberto Bressan, Maria Chiri, and Najmeh Salehi’s work gave us the impetus to consider the tragedy of the commons from the point of view of traveling waves [2].

Numerical approximations of optimal solutions for systems with multiple fishers are generally infeasible due to their exponential complexity with respect to number of agents. A contemporary alternative is to assume an infinite number of fishers, which leads to a mean field game formulation [6, 11]. This approach is especially relevant for modeling the tragedy of the commons. One key factor in this scenario—besides individual greed—is the sheer number of fishers. As this number grows, each individual's relative impact on the overall fish population becomes smaller — thus reducing their incentive to consider the negative consequences of their actions. Mathematically, we assume that each fisher attempts to solve the harvesting problem

\[\underset{\alpha}{\sup}\int^{+\infty}_0 \underbrace {e^{-\lambda t}}_{\textrm{Discount  factor}} \bigg(\underbrace {\theta(y(t),t)}_{\textrm{Harvested  fish}}-\underbrace{\alpha(t)^2}_{\text{Cost}}\bigg) dt \; \textrm{ subject to } \begin{cases} \frac{d}{dt}y(t)=\alpha(t) \\ y(0)=y_0 \end{cases}.\]

This mathematical expression indicates that fishers prefer early profits, favor locations with large amounts of fish, and must pay a cost to change locations (see Figure 2). As we already mentioned, each fisher has an infinitesimal impact on the overall population of fish. However, the resulting density of harvesters, which we call \(m\), does affect the population:

\[\partial_t \theta-\partial_{xx}\theta=f(\theta)- \underbrace{m(x,t)\theta}_{\textrm{Harvested  fish}}.\]

Since every harvester is rational and solves the above optimization problem, the density of fishermen should evolve according to a continuity equation, with a vector field stemming from the optimization. This setup naturally involves a Hamilton-Jacobi equation based on Bellman’s dynamic programming principle. Within this setting, any solution of the following equations is a mean-field Nash equilibrium:

\[\begin{cases} \partial_t \theta-\partial_{xx}\theta=f(\theta)-m\theta, \quad &\theta(0)=\theta_0 \\ \partial_t m + \partial_x(2\partial_xVm)=0, \quad &m(0)=m_0 \\ -\partial_tV+\lambda V-|\partial_xV|^2=\theta \quad &V(+\infty)=0. \end{cases}\]

Assume that without fishermen, the population survives (see Figure 3a). Does a situation exist wherein the infinite number of agents—although acting rationally—can extinguish the population? And can we use the framework of traveling waves (which is justified due to their central role in reaction-diffusion equations) to identify solutions to the latter system that take the form of an extinguishing traveling wave (as in Figure 3b)?

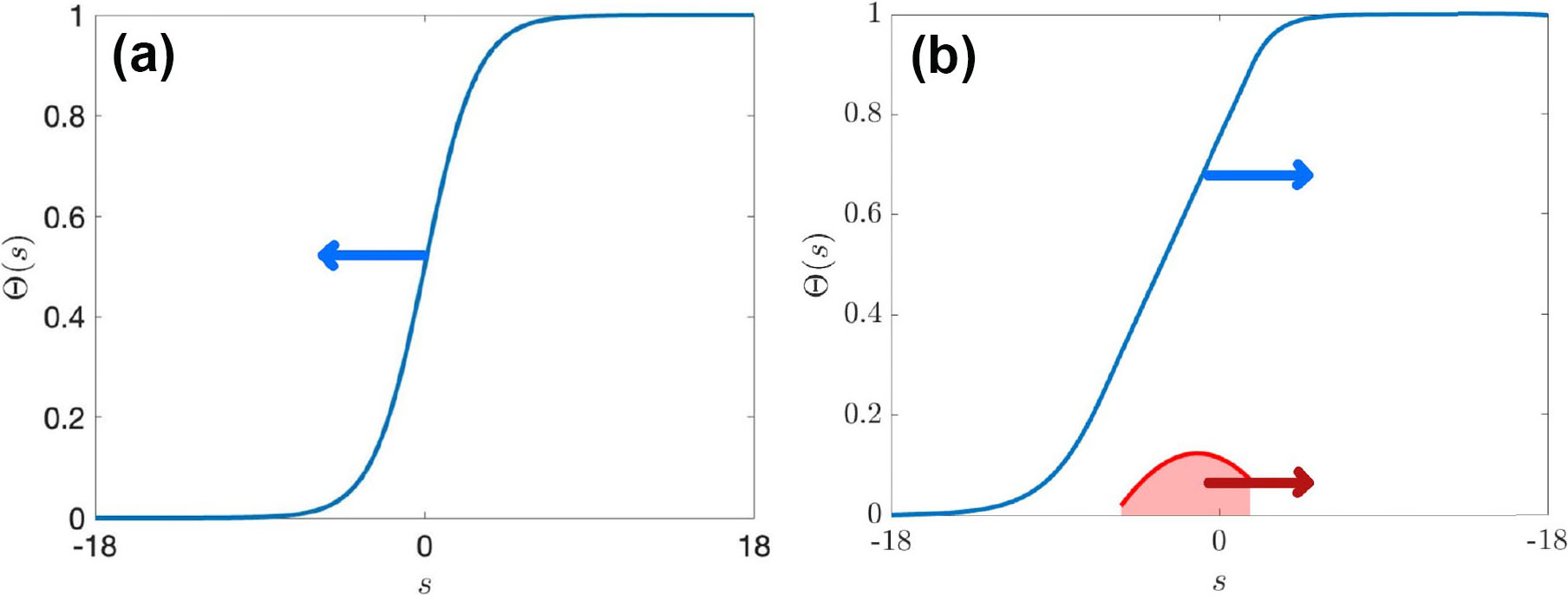
In recent work, we proved the possibility of such situations and demonstrated that a common management structure can lead to higher rewards and may even avoid extinction [9]. Much like in Figure 1, the total catch of fish alone cannot sufficiently predict the collapse of the species in a traveling wave scenario, as this quantity remains constant over time.

Further unexplored avenues lie in this interplay between spatial population dynamics and game theory; these directions could give rise to new aspects of phenomenology and elucidate some of the principles of the tragedy of the commons. For instance, we explored the long-time behavior of a class of harvesting games and realized that they converge to solutions of a particular system called the ergodic system [8]. When paired with an analysis of these particular solutions, the convergence allows us to quantify the tragedy of the commons whenever this convergence holds.

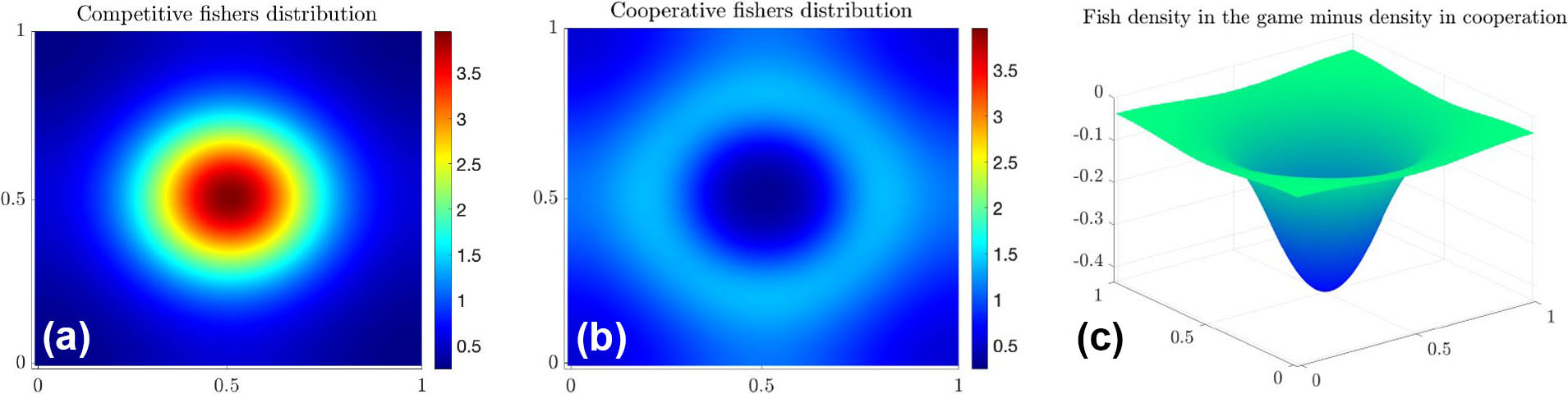
As part of ongoing work, we also derived a system that characterizes the optimal strategy for a fleet of fishers who cooperate rather than compete (see Figure 4). Comparing solutions in both cooperative and competitive contexts yielded three significant conclusions: (i) Both the overall number of living fish and the total catch are higher in the cooperative case; (ii) public policy (in the form of fishing regulations) can incentivize selfish fishers to act cooperatively in their own interests; and (iii) in some instances, cooperative solutions closely resemble protected fishing-free areas.

The third conclusion is especially promising for practical applications, as protected areas represent the simplest and most common form of public policy to regulate fishing. For instance, at the United Nations Biodiversity Conference in December 2022, 192 countries committed to protect 30 percent of the seas and oceans by 2030. However, delineating the boundaries of these protected areas is challenging in practice. Our work has the potential to offer significant insights in this area.

Domènec Ruiz-Balet delivered a minisymposium presentation on this research at the 2023 SIAM Conference on Control and Its Applications, which took place in Philadelphia, Pa., last year.

References
[1] Bliman, P.- A., & Vauchelet, N. (2017). Establishing traveling wave in bistable reaction-diffusion system by feedback. IEEE Control Syst. Lett., 1(1), 62-67.
[2] Bressan, A., Chiri, M.T., & Salehi, N. (2022). On the optimal control of propagation fronts. Math. Models Methods Appl. Sci., 32(6), 1109-1140.
[3] Fife, P. C., & McLeod, J.B. (1977). The approach of solutions of nonlinear diffusion equations to travelling front solutions. Arch. Rational Mech. Anal., 65, 335-361.
[4] Fisher, R.A. (1937). The wave of advance of advantageous genes. Ann. Eugen., 7(4), 355-369.
[5] Hardin, G. (1968). The tragedy of the commons: The population problem has no technical solution; it requires a fundamental extension in morality. Science, 162(3859), 1243-1248.
[6] Huang, M., Malhamé, R.P., & Caines, P. E. (2006). Large population stochastic dynamic games: Closed-loop McKean-Vlasov systems and the Nash certainty equivalence principle. Commun. Inf. Syst., 6(3), 221-252.
[7] Huxley, T. H. (1884). Inaugural address, Fisheries Exhibition, London (1883). Fisheries exhibition literature (Vol. XIV). London, England: William Clowes and Sons, Ltd.
[8] Kobeissi, Z., Mazari-Fouquer, I., & Ruiz-Balet, D. (2024). Mean-field games for harvesting problems: Uniqueness, long-time behaviour and weak KAM theory. Preprint, arXiv:2406.06057.
[9] Kobeissi, Z., Mazari-Fouquer, I., & Ruiz-Balet, D. (2024). The tragedy of the commons: A mean-field game approach to the reversal of travelling waves. Nonlinearity, 37(11), 115010.
[10] Kolmogorov, A.N., Petrovsky, I.G., & Piskunov, N.S. (1937). Étude de l’équation de la chaleur avec augmentation de la quantité de matiere et son applicationa un probleme biologique. Bull. Univ. Moskow, Ser. Internat., Sec. A, 1, 1-25.
[11] Lasry, J.-M., & Lions, P. -L. (2007). Mean field games. Jpn. J. Math., 2(1), 229-260.