The Impact of Generative Models and Social Choice Theory in Elections

A generally accepted principle of democracy is that the political institutions that make impactful decisions should adequately represent the will of the people. During an invited talk at the 2024 SIAM Conference on Mathematics of Data Science (MDS24), which took place last October in Atlanta, Ga., Moon Duchin of Cornell University employed a data science lens to analyze several efforts that seek to preserve and uphold that will within society.

Through a series of vignettes about her research and work as a political consultant, Duchin explored the concepts of electoral districting and social choice theory. Electoral districting involves the fair definition of geographic boundaries of individual subsets within a state, each of which has elected representatives who express their constituencies’ interests in higher-level legislative processes. Social choice theory, in turn, examines the challenges that are associated with making collective decisions about important issues from a list of options (e.g., selecting a mayor from a ballot or passing constitutional amendments). This theory is based on the idea that different voting rules—i.e., algorithms that aggregate many opinions into a single decision—can yield qualitatively different outcomes.

The Mathematics of Elections

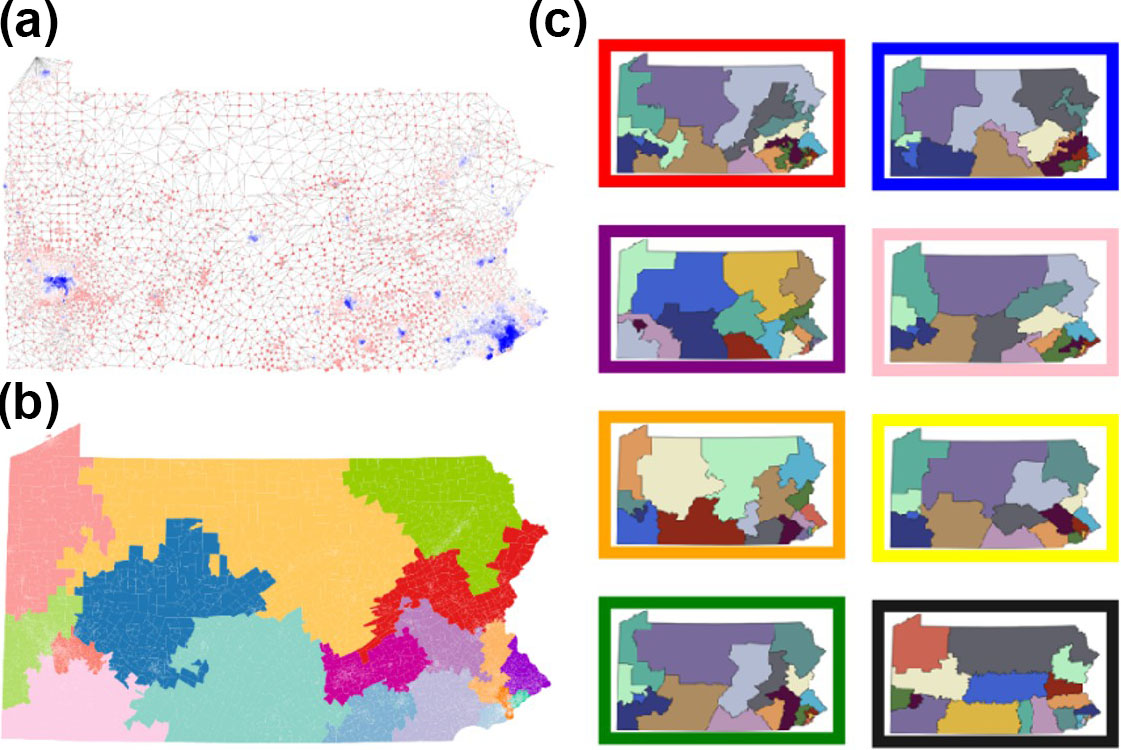
Because political representation in the U.S. is both multiscale and heterogenous, the details of political processes are remarkably complex. One prominent issue is gerrymandering, which refers to a political party’s manipulation of electoral district boundaries to maintain power or minimize the influence of particular factions (e.g., political or racial groups). Growing interest in historical and current incidences of gerrymandering has inspired a bevy of mathematical models that map two-dimensional shapes to numerical scores of compactness. Although this methodology is mathematically rigorous, it often struggles to translate into political impact. However, Duchin’s recent efforts to quantify gerrymandering have successfully contextualized human-drawn maps; Figure 1 provides an ensemble of graph partitions that she generated based on the adjacency of small political units.

An interrelated source of tension in the U.S. is the plurality voting system, wherein voters select only one option on their ballot per race and the candidate in each category with the largest aggregated proportion of votes ultimately wins. In this system, elections with three or more choices/candidates can cause “vote splitting” among mostly aligned voting groups. In short, options that share certain similarities draw votes away from either other and eventually lead to two-party systems in a phenomenon that is known as Duverger’s law [3, 5]. Given this suboptimality in U.S. electoral processes, voters frequently express frustration at the misalignment of political strategy with the needs of the population. The study of alternative voting schemes has its own mathematical history that is often steeped in axiomatic statements of system features and “impossibility” theorems.

Sampling and Evaluating Electoral District Maps

A major focus of Duchin’s work is the automated generation and evaluation of feasible electoral district maps that represent consistent geographical regions. A common way to communicate the boundaries of geographic regions is through nontopological data storage formats called shapefiles, which describe boundaries with sequences of longitude and latitude coordinates. However, the federated, heterogeneous nature of the U.S. means that data curation and management practices can vary wildly on the county, tract, and census block level within a single state; some data may also be stored in unexpected formats. These inconsistencies manifest as a complicated data synthesis problem. In order to build accurate maps and enforce explainable and trustworthy evaluations of the political ecosystem, researchers must have access to accurate data [2].

Using a consistent dual adjacency graph, Duchin illustrated the objective of Markov-chain-based map generation during her MDS24 talk. Given a desired number of precincts \(n\), the goal is to quickly partition a graph into \(n\) disjoint subgraphs—i.e., by labeling every vertex from the choices \(\{1,...,n\}\)—subject to a list of constraints (e.g., connectedness and legality). The ability to capture feasible districts relies on the performance of iterative processes on these subgraphs. One approach hinges on classical Ising models from statistical physics, wherein “flips” are performed one vertex at a time to slowly evolve from the initial condition. A simplified Ising-based “flip” iteration occurs in two steps. First, one must identify an edge \(k\) that connects vertices \(i\) and \(j\) with different labels \(l_i\) and \(l_j\). The next step is to randomly choose a vertex and replace its label with that of the other vertex; modifications can be made to account for the preservation of size or other constraints.

To improve upon the Ising method, Duchin and her collaborators proposed the so-called recombination (ReCom) algorithm (see Figure 2) [1]. The ReCom algorithm restructures two adjacent districts/subgraphs \(I\) and \(J\) that are only constrained by size preservation. The vertices of these subgraphs—associated with labels \(l_I\) and \(l_J\)—are used to take a “union” of the subgraphs. ReCom then constructs a spanning tree of this new subgraph. Next, one must identify a balanced edge of this spanning tree, i.e., an edge whose removal would produce two (approximately) equal-size subgraphs. The vertices of these new subgraphs are reassigned labels \(l_I\) and \(l_J\).

Duchin explained that the ReCom approach is provably fast because the computational time of an iteration is dominated by the computation of spanning trees — a classical graph theoretic problem with runtime \(O(E \log(E))\), where \(E\) is the number of edges in the subgraph. On both rectangular grids and realistic geometries, several hundred iterations of ReCom can sufficiently generate a well-mixed districting map from an arbitrary initial condition.

After illustrating the concept on a rectangular grid, Duchin applied the fast ReCom algorithm to assess a set of eight traditionally drawn proposed maps for the state of Pennsylvania. She employed a function that assigns a political bias score to a proposed district map and constructed a histogram across an ensemble of ReCom-generated maps, ultimately assisting with the Pennsylvania Supreme Court’s selection of a map in 2022 as part of Carter v. Chapman [4]. Duchin also served as an expert witness and amicus curiae in the Wisconsin Supreme Court in 2021 during Johnson v. Wisconsin Elections Commission, and in the U.S. Supreme Court cases Rucho v. Common Cause in 2019 and Allen v. Milligan in 2022.

Although this work was inspired by specific real-world needs, Duchin noted that the field of mathematical political science continues to evoke many new questions about Markov chain sampling and graph partitioning. It also highlights broad, important challenges in network theory and data science that pertain to topics like clustering and community detection.

Social Choice Theory and Voting

The second part of Duchin’s MDS24 presentation focused on social choice theory and voting theory, namely the ways in which a collection of people can arrive at a decision from a list of possible choices.

Anyone who teaches an undergraduate math course with a module on voting theory is likely familiar with Arrow’s impossibility theorem, which rules out all possible voting systems that satisfy a particular set of axioms. When asking for unanimity and independence properties, Arrow’s theorem suggests that the only valid system is a dictatorship. Disallowing dictatorships hence leads to the “impossibility” in social choice theory of requiring a voting system to preserve all axioms.

Beyond plurality vote, experts have proposed many systems that may provably satisfy various properties. One of these alternatives—and perhaps the most famous—is ranked choice voting. Duchin explored this framework in the context of the 2021 New York City mayoral campaign, during which ranked choice voting led to the election of Eric Adams (though Adams was also the plurality leader in all rounds of voting). New York City’s ranked choice voting methodology is an iterative process wherein voters rank the available choices and submit their full listings. Based on the aggregate tally of voters’ first choices, the lowest ranked choice is eliminated and votes for that least popular choice are automatically reallocated to the remaining choices according to voters’ rankings. The process repeats until only one winning candidate is left.

Duchin also overviewed a handful of alternate schemes with surprisingly nice properties, including randomly selected dictator. Another interesting scheme is plurality veto: a subtractive system that tallies “positive” votes in a first round, then iteratively subtracts points from candidates based on negative preferences until a single option with a nonzero tally remains.

Finally, Duchin shared her perspective on the notion of axioms in social choice theory. A recent axiom of note is proportionality, which asserts that the selection of preferences should somehow reflect voters’ intersectional makeup. Additionally, Duchin mentioned that she would like to see the field of mathematical political science move away from the rigid demands of binary properties—as in Arrow’s axioms—and respond more in terms of tendencies, i.e., the typical behaviors of these axioms (such as those in Arrow’s framework, or more modern axioms like proportionality) rather than worst-case behaviors.

Applied mathematicians clearly have important roles to play as experts, modelers, and evaluators of existing political systems. Duchin repeatedly emphasized the bidirectional nature of this work; fundamental research contributes to practical algorithms and impacts society while simultaneously revealing open questions in fields such as graph theory, numerical analysis, and mathematical data science. This type of two-way relationship comprises the heart of applied mathematics as a discipline. We look forward to future contributions from Duchin and other researchers as they continue to pursue fair political representation and effect positive societal change.

References
[1] DeFord, D., Duchin, M., & Solomon, J. (2021). Recombination: A family of Markov Chains for redistricting. Harvard Data Sci. Rev., 3(1). 
[2] Duchin, M., & Tenner, B.E. (2024). Discrete geometry for electoral geography. Polit. Geogr., 109(4), 103040.
[3] Palfrey, T.R. (1988). A mathematical proof of Duverger’s law (Social science working paper 688). Pasadena, CA: California Institute of Technology.
[4] Previti, E., & Meyer, K. (2018). In Pennsylvania, new court-drawn voting map could shift advantage to Democrats. NPR. Retrieved from https://www.npr.org/2018/02/19/586668315/court-decides-pennsylvania-voting-map.
[5] Riker, W.H. (1982). The two-party system and Duverger’s law: An essay on the history of political science. Am. Polit. Sci. Rev., 76(4), 753-766.